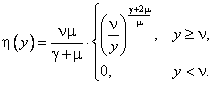Режим сбалансированного инфляционного роста экономики

Среди траекторий модели, описывающих эволюцию экономики, особый интерес представляет режим сбалансированного инфляционного роста (РСИР), в котором натуральные показатели растут с постоянным темпом , цены на производимый в экономике продукт изменяются в соответствии с постоянным темпом , а соответственно финансовые показатели √ . Большой спектр исследований, проведенных методами системного анализа развивающейся экономики, показал, что в моделях, описывающих эволюцию развивающейся экономики, режим сбалансированного инфляционного роста является ╚притягивающим╩ для большинства траекторий соответствующих систем. Анализ модели в режиме сбалансированного инфляционного роста позволяет методами сравнительной статики исследовать макроэкономические показатели состояния экономики и энергетики в различных сценариях, определяемых вариантами государственной политики в отношении отраслей ТЭК.

В режиме сбалансированного инфляционного роста

.═══════════════════════════════════════ ═════════════════════ (108)

Исследуем РСИР для случая, когда

.═══════════════════════════════════════════════════════════ ═════════════════════ (109)

Выполнение первых двух неравенств обусловлено тем, что в современных российских условиях характерное время между моментами реализации продукции производителем оказывается меньше года, что соответствует значению параметра . Учитывая, что , получаем первые два неравенства. Третье неравенство является естественным ограничением на темп роста экономики - темп роста производства должен превосходить темп выбытия. В современных российских условиях это ограничение представляется справедливым. Наконец, последнее условие характеризует особенность функционирования российского производства. В современных условиях долгосрочный кредит оказывается для производителя зачастую дешевле краткосрочного, так как выдается в основном на льготных условиях хорошо известным ⌠клиентам■. Анализ модифицированной модели Хаутеккера-Иохансена [2,3] показал, что именно при таком условии возникает наблюдаемое в реальных российских условиях неэффективное использование производственных мощностей - средний коэффициент загрузки мощности оказывается в интервале от нуля до единицы.

Обозначим

,══════════════════════════════════════════════════════════════════════════════ ═════════════════════ (110)

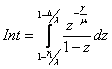.══════════════════════════════════════════════════════════════════════════ ═════════════════════ (111)

В современных условиях система коммерческих банков функционирует по схеме I. Поэтому естественно находить РСИР также для этого случая.

По схеме I система коммерческих банков устанавливает процент ═исходя из максимизации процентов по краткосрочным кредитам производству с учетом риска (84)

.══════════════════════════════════════════════════════════════════════════════════════════ (84)

В режиме сбалансированного инфляционного роста (108), с учетом ограничений (109), из (2) и (12) получим, что величина выданных коммерческими банками краткосрочных кредитов определяется выражением

,════════════════════════════════════════════════════════════ ═══════════════ ═══════════ (113)══

где .══════════════ ═══ ═══════════════════════ (114)

Подставим выражение для ═в (84) и приравняем нулю производную по ═от выражения (84). Решение полученного уравнения определяет зависимость

,═══════════════════════════════════════════════════════════════════════════════════ ═════════════════════ (115)

которая всюду далее будет подразумеваться под символом .

В режиме сбалансированного инфляционного роста величина выданных долгосрочных кредитов , определяемая выражением (13), с учетом (1), имеет вид

,═════════════════════════════════════════════════════════════════════ ════════════════════ (116)

где ═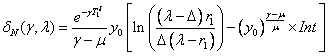.═════════════════ ════════════════════ (117)

Из (7), (8) (с учетом (6)) получим выражения для выпуска и затрат первой отрасли на сбалансированном росте

,═════════════════════════════════════════════════════════════════════════════ ═════════════════════ (118)

,

где

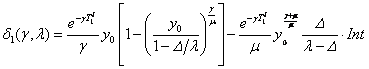;══════════════ ═════════════════════ (119)

════════════════ ═════════════════════ (120)

Обозначим . ════════════════════════════ ═══════════════════════════ (121)

Далее для краткости записи аргументы функций ═указываться не будут.

С учетом полученных соотношений из финансового баланса (9) и ограничения ликвидности (11) для первой отрасли находим зависимость темпа инфляции ═от темпа роста ═и параметра .

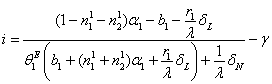.═══════════════════════════ ═══════════════════════════ (122)

Зависимость (122) темпа инфляции от темпа роста при фиксированном ═будем называть технологической кривой.

В режиме сбалансированного роста выпуски 2-й и 3-й отраслей , затраты фондообразующего продукта ═и текущие производственные затраты ═() определяются выражениями

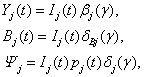═══════════════════════════════════════════════════════════════════════ ═════════════════════ (123)

где

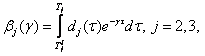════════════════════════════════════════════════════════ ═════════════════════ (124)

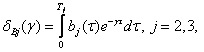════════════════════════════════════════════════════════ ═════════════════════ (125)

═════════════════════════════════════════════════════════ ═════════════════════ (126)

════════════════════════════════ ════════════════════ ═ (127)

При этом текущие затраты отрасли ═() определяются суммой затрат всех отраслей на производство продукции отрасли , т.е.

══════════════════════════════════════════════════════════════════════════ ═════════════════════ (128)

где величины ═════════════════════ ═══════════════════════════ (129)

определяют затраты продукции -й отрасли при производстве продукции -й отрасли.

Коэффициенты , ══определяются пропорцией коэффициентов текущих капитальных затрат и текущих затрат на выпуск в электроэнергетике, при этом средний коэффициент материалоемкости продукции электроэнергетики равен . Исходя из экспертных оценок структуры затрат в электроэнергетике (см. [6]) в расчетах по модели предполагалось, что .

Обозначим [1], ═════════════════════════ ═══════════════════════════ (130)

Из финансовых балансов и ограничений ликвидности для 2-й и 3-й отраслей определяются величины налоговой нагрузки в электроэнергетике ═(2-я отрасль) и доли заработной платы в НГК ═(3-я отрасль)

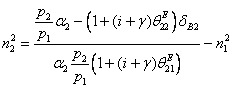,════════════════════════════════════════════════ ═════════════════════ (131)

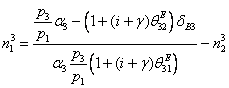.════════════════════════════════════════════════ ══════════════════════ (132)

Из финансового баланса торгового посредника═ и соответствующего ограничения ликвидности, с учетом (41) получим

,═══════════════════════════════════════════════════════════ ═══════════════════════════ (133)

где

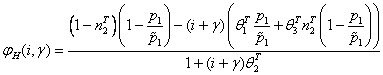.═════ ═════════════════════ (134)

Аналогично, из финансового баланса и ограничения ликвидности импортера получим

,══════════════════════════════════════════════════════════════════════ ═════════════════════ (135)

где

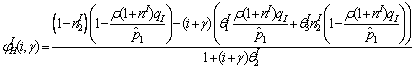.════════════════════════ (136)

Перепишем соотношение (68) в виде, ═══════════════════════ ═════════════════════ (137)

где .══════════════════════════════════════════════════════════════ ═════════════════════ (138)

Из соотношения (85), с учетом (113) и (137), получаем выражение для прибыли коммерческих банков в режиме сбалансированного инфляционного роста

.══════════════════════════════════════════════ ══════════════════════════ (139)

Используя полученные соотношения, из финансового баланса и ограничения ликвидности домашних хозяйств (42) и (50) при условии , с учетом (35), (36), находим выражение для расходов населения

,═════════════════════════════════════════════════════════════ ═════════════════════ (140)

где

,═════════════════════════════════ ═════════════════════ (141)

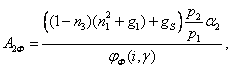══════════════════════════════════════════════════ ═════════════════════ (142)

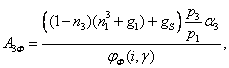══════════════════════════════════════════════════ ═════════════════════ (143)

══════════ (144)

Из уравнения изменения золотовалютных резервов (88) получим

,═══════════ ═════════════════════ (145)

где

,

,

,

.

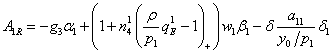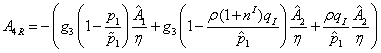Из баланса государственного бюджета (78) и соответствующего ограничения ликвидности (79) определяется государственное потребление первого продукта

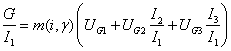,═════════════════════════════════════════════════ ═════════════════════ (146)

где ,

,

,

,

,

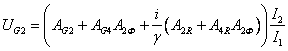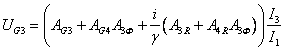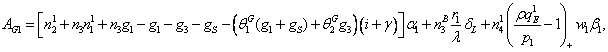
Из уравнения для определения цены на продукт первого сектора (92) получим связь темпа инфляции с темпом роста и величиной параметра , которую мы будем называть рыночной кривой

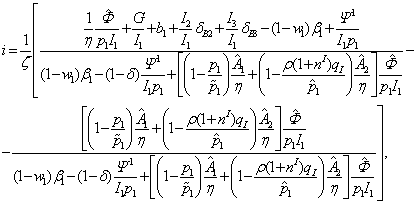════════════════════════ ═(147)

где .

Уравнения технологической кривой (122) и рыночной кривой с учетом полученных выше выражений для входящих в них пропорций определяют связь темпа инфляции, темпа роста и параметра неэффективности , если определены входящие в рыночную кривую пропорции инвестиций ═как функции, зависящих от .

Для определения пропорций инвестиций воспользуемся материальными балансами энергопроизводящих отраслей, которые в режиме сбалансированного инфляционного роста имеют вид ═где ═- спрос на продукцию отраслей.

Из материального баланса электроэнергетики имеем , ,

.

Из материального баланса НГК

.

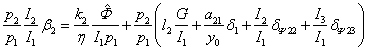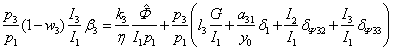Из двух последних соотношений, учитывая (146), получим

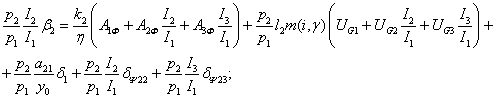
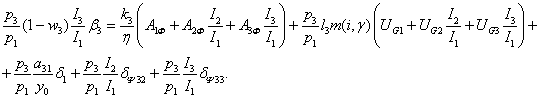
Таким образом, структура инвестиций 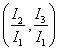═является решением следующей линейной алгебраической системы:

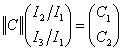,════════════════════════════════════════════════════════════════════════════ ═════════════════════ (148)

где

,

,

,

,

,

,

.

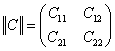Итак, подставляя в рыночную кривую решение системы для определения пропорции инвестиций, получим, что технологическая (122) и рыночная кривая (147) определяют темп инфляции и темп роста в зависимости от значения параметра неэффективности .

Следует отметить, что в режиме сбалансированного роста система коммерческих банков функционирует по схеме I. Поэтому расчеты РСИР достоверны, если только , т.е. при проведении расчетов требует контроля знак разности

Замыкающим предположением модели является правило расчета параметра неэффективности . Согласно уравнению, описывающему формирование запасов (94), имеем выражение для запасов в соответствии с описанием модели в режиме сбалансированного роста

═════════ (149)

С другой стороны, формирование запасов нереализованной продукции можно найти, воспользовавшись описанием особенностей функционирования энергопотребляющео сектора. Для этого найдем отношение среднего запаса продукции 1-й отрасли к средней выручке в режиме сбалансированного инфляционного роста, используя полученное в работе [3] из (106) выражение для распределения мощностей по себестоимости в рассматриваемом режиме:

Здесь y - себестоимость единицы продукции (), а ═- распределение мощностей по себестоимости.

Подставим выражения для ═и , полученные из задачи о максимизации математического ожидания денежных доходов за цикл деятельности производственной единицы между двумя моментами реализации продукции. Тогда получаем следующие два выражения для отношения среднего запаса продукции 1-й отрасли к средней выручке.

1) Если процент по краткосрочному кредиту меньше процента по долгосрочному кредиту, т.е. , то

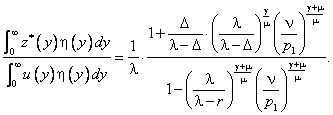
2) Если процент по краткосрочному кредиту больше процента по долгосрочному кредиту, т.е. , то

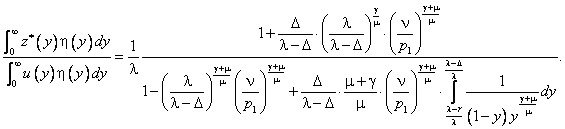
Учитывая, что левая часть последнего соотношения определяет отношение запасов к выпуску, в режиме сбалансированного инфляционного роста получим уравнение относительно

,

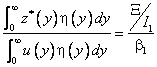т.е.

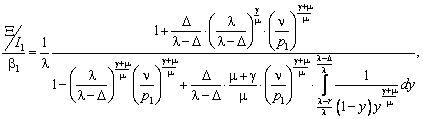═════════════════ (150)

где величина запасов ═определена в силу (149).

Итак, система уравнений модели в режиме сбалансированного инфляционного роста сводится к системе пяти уравнений (122), (147), (148), (150) относительно переменных . Определение этих переменных дает возможность вычислять макроэкономические характеристики выделенных в модели экономических агентов, такие как доля добавленной стоимости отраслей в ВВП, доля потребления населения в ВВП, доля потребления государства в ВВП, доля ЗВР в ВВП и др.

---

[1] Далее в формулах аргумент функций ═указываться не будет.