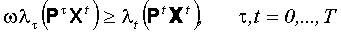 (14)
(14)
Как правило, торговая статистика удовлетворяет гипотезе о рациональном поведении в течение десятилетий. В худшем случае требуется отбросить несколько временных точек. При этом удавалось выявить внушительную иерархию индексов потребления, т.е. провести многоступенчатое агрегирование торговой статистики. При этом ряды индексов потребления и индексов цен мелких групп товаров служат торговой статистикой для построения индексов более крупных групп. Но свидетельствуют ли исключенные точки об изменении в эти моменты структуры потребительского спроса или о каких-то погрешностях в статистике? Для изучения этого вопроса было бы удобно иметь какой-то естественный количественный показатель "нерациональности" статистики. При выборе такого показателя следует принять во внимание следующее соображение. Основным источником погрешностей торговой статистики является, по-видимому, то, что представленные в ней несколько сотен товаров являются по существу товарными группами, цены которых представляют собой некоторые эмпирически построенные товароведами индексы цен. Оказывается, что при многоступенчатом агрегировании, даже используя непараметрический метод на каждой стадии, можно из статистики, удовлетворяющей условию рациональности, получить на некотором шаге статистику, не удовлетворяющую этому условию. Это связано с тем, что система неравенств (13) имеет много решений, а алгоритм Варшалла - Флойда выбирает какое-то одно из них, не обязательно то, которое пригодно для дальнейшего агрегирования.
В [8,15] было разработано обобщение непараметрического метода, применимое при нарушении гипотезы о рациональном поведении. Именно, вместо системы (13) предлагается решать систему
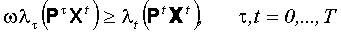 (14)
(14)
при некотором ![]() >= 1.
>= 1.
Очевидно, что с ростом ![]() множество решений системы расширяется. Если система (13) не имеет положительного решения, то существует
множество решений системы расширяется. Если система (13) не имеет положительного решения, то существует ![]() , которое является нижней границей множества значений
, которое является нижней границей множества значений ![]() , для которых разрешима система (14).
, для которых разрешима система (14).
Предложение 1. При ![]() система неравенств (14) имеет единственное (с точностью до множителя) положительное решение. Это решение вместе с
система неравенств (14) имеет единственное (с точностью до множителя) положительное решение. Это решение вместе с ![]() однозначно определяется системой уравнений
однозначно определяется системой уравнений
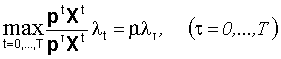 (15)
(15)
Как показано в [14], это предложение следует из того, что величину можно рассматривать как аналог наибольшего собственного значения (числа Фробениуса - Перрона) матрицы индексов цен Пааше
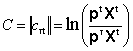 (16)
(16)
если рассматривать матричные операции в полукольце
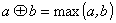 ,
,
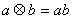
над ![]()
Уравнение (15) в этих обозначениях принимает вид
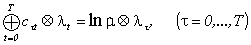
Существование положительного решения системы (13) можно интерпретировать как идемпотентный аналог свойства продуктивности матрицы (16) (см. [16]). Тогда эквивалентность утверждений 2 и 3 из теоремы Африата - Вериана интерпретируется как идемпотентный аналог известного критерия продуктивности (см. [16]) в терминах сходимости "геометрической прогрессии"
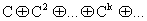 (17)
(17)
где степени матрицы понимаются в смысле идемпотентных операций. Заметим, что алгоритм Варшалла - Флойда заключается в вычислении идемпотентной суммы ряда (17). Рассматриваемый показатель ![]() естественным образом связан и со "степенью неинтегрируемости" дифференциальной формы P(X) dX.
естественным образом связан и со "степенью неинтегрируемости" дифференциальной формы P(X) dX.
Предложение 2. Пусть торговой статистике { pt, Xt}, t = 0,... ,T отвечает показатель ![]() и неотрицательная, непрерывно дифференцируемая обратная функция спроса P(X) на
и неотрицательная, непрерывно дифференцируемая обратная функция спроса P(X) на ![]() , такая что :
, такая что :
pt = P( Xt );
P(X) X > 0 при любых 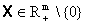 ;
;
![]() при любых
при любых ![]() ,
, 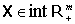 , i,j = 1, ... , m (условия отделимости);
, i,j = 1, ... , m (условия отделимости);
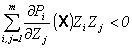 для любого Z = ( Z1, ... , Zm ) != 0 такого, что P ( Z ) Z = 0 (закон Хикса).
для любого Z = ( Z1, ... , Zm ) != 0 такого, что P ( Z ) Z = 0 (закон Хикса).
Тогда справедливы следующие утверждения:
1. Если P ( X ) удовлетворяют гипотезе о рациональном поведении, то
i). дифференц. форма P(X) dX имеет интегрирующий множитель 1/Q( P( X ) ) ;
ii). для любого дифференцируемого двумерного многообразия D из ![]() с кусочно-гладкой границей dD справедливо равенство
с кусочно-гладкой границей dD справедливо равенство
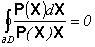 ;
; 2. Если дифференциальная форма P(X) dX не имеет интегрирующего множителя в окрестности некоторой точки 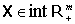 , то:
, то:
i). В любой окрестности этой точки существует дифференцируемое двумерное многообразие D с кусочно-гладкой границей dD такое, что
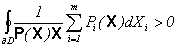 ;
; ii).
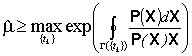 ;
;где max берется по всем упорядоченным множествам моментов времени 0 <= t1 <= t2 <= ...<= T, a Г ( { tk } ) - контур, составленный из отрезков, последовательно соединяющих точки 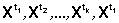 .
Док-во этого утверждения приведено в [14].
.
Док-во этого утверждения приведено в [14].
Итак, если торговая статистика не удовлетворяет (12) и, следовательно, стандартный непараметрический метод оказывается неприменимым, то можно предложить следующее его обобщение. Вместо системы линейных неравенств (13) , не имеющей положительных решений, предлагается определять индексы цен из решения модифицированной системы (14), которая имеет положительные решения при значениях параметра ![]() , превышающих показатель
, превышающих показатель ![]() нарушения торговой статистикой гипотезы о рациональности поведения. Из множества всех положительных решений системы (14) алгоритм Варшалла - Флойда выбирает конкретное решение, которое, вообще говоря, изменяется при изменении параметра
нарушения торговой статистикой гипотезы о рациональности поведения. Из множества всех положительных решений системы (14) алгоритм Варшалла - Флойда выбирает конкретное решение, которое, вообще говоря, изменяется при изменении параметра ![]() . Среди множества положительных решений системы (14) имеется одно выделенное решение, которое удовлетворяет (14) при всех
. Среди множества положительных решений системы (14) имеется одно выделенное решение, которое удовлетворяет (14) при всех 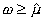 . Это решение является идемпотентным аналогом вектора Фробениуса - Перрона, и его было бы естественно использовать при вычислении экономических индексов. Это решение можно найти из (14), если положить
. Это решение является идемпотентным аналогом вектора Фробениуса - Перрона, и его было бы естественно использовать при вычислении экономических индексов. Это решение можно найти из (14), если положить 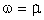 . При использовании многоступенчатых схем вычисления экономических индексов удобно установить значение
. При использовании многоступенчатых схем вычисления экономических индексов удобно установить значение ![]() одним для всех рассматриваемых подгрупп номенклатуры товаров. Однако значения показателя
одним для всех рассматриваемых подгрупп номенклатуры товаров. Однако значения показателя ![]() для различных подгрупп оказывается разным.
для различных подгрупп оказывается разным.
Интересно изучить, насколько изменяются решения, получаемые алгоритмом Варшалла - Флойда, при изменении ![]() . Для исследования этого вопроса естественно обратиться к численным экспериментам.
. Для исследования этого вопроса естественно обратиться к численным экспериментам.
Далее 4.2. Прогнозирование в рамках обобщенного непараметрического метода