 |
Согласно параметрическому методу выбирается класс функций, внутри которого ищется функции полезности (индекс продукта). Например, в [2] рассматривается класс функций полезности
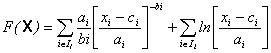 |
где ci>0, ai>0, bi>-1 - параметры функции полезности,
|
|
Функции из этого класса, вообще говоря, не являются положительно однородными первой степени. Рассматривая задачу о максимизации функции полезности F(X) при бюджетном ограничении
F(X) -> max,
PX <= Y,
X > 0, где Y - денежные средства, расходуемые на приобретение товаров, находим функции спроса X (решение задачи в зависимости от P и Y):
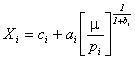 |
где μ определяется из уравнения:
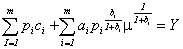 |
Исходной информацией является торговая статистика или временные ряды {pt, Xt}, задающие функции спроса в конечном числе точек. В случае параметрического метода параметры подбираются таким образом, чтобы временной ряд лучше всего соответствовал предполагаемым функциям спроса.