(in Russian)

Fast Algorithms and the FEE Method ^*

E. A. Karatsuba

I. FAST ALGORITHMS

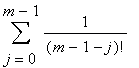
        The field of computational mathematics, which is called Fast Algorithms, was born in 1960. By an algorithm, not formalizing this concept, we mean a rule or a way of computation.

        We assume that numbers are written in the binary form, the signs of which 0 and 1 are called bits.

Def. 1. Writing down of one of the symbols 0, 1, +, –, (, ), putting together, subtraction and multiplication of two bits is called an elementary operation or a bit operation.

        Fast Algorithms is the field of computational mathematics that studies algorithms of evaluation of a given function with a given accuracy, using as few bit operations as possible. Thus the algorithms, which, can be called fast ones, are real algorithms. Realizing such algorithms in software (and sometimes in hardware) it is possible to increase essentially the computer's efficiency, and sometimes to solve problems of the size that didn't permit a solution by means of ordinary methods of computation. The question of the size of a problem, which can be solved in a certain time with the help of a given computer, leads us to the concept of complexity of computation.

        In what follows, unless otherwise specified, the complexity of calculations means the bit complexity.

        The problem of complexity of computation was first formulated by A. N. Kolmogorov (1956) [37], [38], who emphasized at the same time, that ‘... the series of my works on information theory was created in the 50s and 60s under a strong influence of publications by Norbert Wiener and Claude Shannon ...’

        Before we introduce the concept of complexity of computation, we define what it means to evaluate a function at a given point. Consider the simplest case: let y = f(x) be a real function of a real argument  x, a ≤ x ≤ b,  and assume that  f(x)  satisfies on  (a,b)  the Lipschitz condition of order  α, 0 < α <1,  that is for  x₁, x₂ ∊ (a,b):

|f(x₁) – f(x₂)| ≤ |x₁ – x₂|^α.

Let  n  be a natural number.

Def. 2. To compute the function  y = f(x)  at the point  x = x₀ ∊ (a,b)  up to  n  digits means to find such a number  A,  that

|f(x₀) – A| ≤ 2^–n.

Def. 3. The total number of bit operations sufficient to compute the function  f(x)  at the point  x = x₀  with accuracy up to  n  digits by means of a given algorithm, is called the complexity of computation of  f(x)  at the point  x = x₀  up to  n  digits. Thus, the complexity of computation of  f(x)  at the point  x = x₀  is a function of  n;  and so are  f(x)  and  x = x₀.

This function is denoted by

        It is clear that  S_f  depends also on the algorithm of calculation and for different algorithms will be different. The complexity of a computation is directly related to the time that the computer needs to perform this computation. For this reason, the complexity is often treated as a ‘time’ function  T(n)  [36].

        The problem of behavior  S_f(n)  as  n → ∞  for a class of functions or for a particular function  f,  was for the first time formulated by Kolmogorov around 1956. Since in computations the four arithmetical operations, namely, addition, subtraction, multiplication and division are used in the first place, one needs to know the number of bit operations sufficient for performing these operations. Definitions 2 and 3 imply that the numbers  x₀  and  A  can be represented in the form of the integral part and  n  binary digits after the binary dot,i.e.,

where  ν_j, μ_j = 0  or  1, j = 1, 2, ... , n.

        Since the integral parts  [A], [x₀]  are fixed and  n → ∞,  the operations are, in fact, performed on  n -digit integers. Therefore, first of all there is a problem of estimating the complexity of calculation of the sum, difference, product, and quotient of two  n -digit integers  a  and  b.  Note that division (with a remainder) reduces to addition, subtraction and multiplication of numbers. To write down the numbers  a  and  b  one needs at least  2n bit operations. Consequently, the complexity of addition (subtraction) of  a  and  b  is not less than  3n  bit operations, and not more (when doing it in an ordinary manner) than  4n  bit operations. Hence, the order of the number of bit operations which are necessary and sufficient for putting together and subtracting is the same.

        In what follows we call the bit operations simply operations, omitting the word bit.

        The next problem is the problem of the total number of bit operations sufficient for computing the product  ab,  or the problem of complexity of multiplication. The function of complexity of multiplication has the special notation  M(n).

        Multiplying two  n -digit numbers in the ordinary school way, ‘in column’, we actually put together in this case  n  n -digit numbers. So for the complexity of this ‘school’ method or ‘ordinary’ method we get the upper bound  M(n) = O(n²).

        In 1956 A. N. Kolmogorov formulated the conjecture, that the low bound for  M(n)  for any method of performing the multiplication is also of order  n²  (the so-called Kolmogorov  ‘n² -conjecture’). The fact that the method of multiplication ‘in column’ has been known at least for 4 thousands years (for example, this method was used by summers), so that if there existed a faster method of multiplication, it would have been most likely already found, was an argument in favour of the  ‘n² -conjecture’.

        In 1960 A. Karatsuba [20], [21], [22] (see also [36]) found a method of multiplication with the complexity bound

and thus disproved the  ‘n² -conjecture’.  Later the method was called ‘Divide and Conquer’; the other names of this method, used at the present, are ‘Binary Splitting’, ‘Dichotomy Principle’ etc.

        The appearance of the method ‘Divide and Conquer’ was the starting point of the theory of fast computations. A number of authors (among them Toom [51], Cook [15], and Schönhage [45]) continued to look for an algorithm of multiplication with the complexity close to the optimal one, and in 1971 Schönhage and Strassen [46], [47] constructed an algorithm with the best known (at present) upper bound for  M(n).

In the construction of this algorithm, apart from ‘Divide and Conquer’, they used the idea of realizing arithmetic operations modulo the Fermat numbers  2²ⁿ+ 1,  and the Fast Fourier Transform.

        On the basis of the method ‘Divide and Conquer’ the algorithms of fast matrix multiplication were constructed. Strassen [50] was the first to find such algorithm in 1970, later these investigations were continued by Coppersmith and Winograd [16], Pan [43] and others.

        Approximately at the same time the first algorithms of calculation of elementary algebraic functions started to appear. As it was already mentioned before, the division of the number  a  by the number  b  with residue, that is the calculation of the numbers  q  and  r  in the formula

is reduced to addition-subtraction and multiplication, and if  a  and  b  are  n -digit numbers, then the complexity of division is  O(M(n)).

        The simplest algorithm of division is to compute the inverse value  1/b  with accuracy up to  n  digits by the Newton method and after that to multiply by  a  using the fast multiplication algorithm.

        Assume that we must find  x = 1/b,  where  1/2 ≤ b ≤ 1  (if this is not true, then multiplying or dividing by  2^N  we obtain the example under consideration). As an initial approximation we take  x₀ = 3/2  and calculate by formula

This method provides sufficiently fast convergence to  1/b,  since from the equality  x_n = 1/b – ε,  it follows  x_n+1 = 1/b – bε².

        For taking the root of  k -th degree from a number, that is for the calculation of  a^1/k,  it is also possible to use the Newton method. Assume  k ≥ 2  is an integer and we must compute  x = a^1/k,  where  a ≥ (k + 1)^k.  We compute  x  by the formula:

Note that multiplying or dividing by  2^kN,  one can always get the condition  a ≥ (k + 1)^k  (sometimes this condition is unnecessary, because the indicated process converges fast for other  a,  either). As an initial approximation it is possible to take, for example, one of the numbers  d  or  d+1,  where  d  is the integer that satisfies the condition  d^k < a ≤ (d + 1)^k.  The complexity of the calculation is also  O(M(n)).

        First fast algorithms of computation of elementary algebraic functions based on the Newton method appear in the works of Cook [15], Bendersky [8] and Brent [11] (see also [36]). Using Newton's method, it is possible to prove also the following theorem ([11]):

Theorem. If the equation  f(x) = 0  has a simple root  ζ ≠ 0,   f(x)  is Lipschitz continuous in the neighborhood  ζ, and we can compute  f(x)  with accuracy up to  n  digits by  O(M(n)j(n))  operations, where  j(n)  is a positive, monotone increasing function for any  x  from a neighborhood of   ζ,  then it is possible to calculate  ζ  with accuracy up to  n  digits also by  O(M(n)j(n))  operations.

        In 1976 Salamin [44] and Brent [11] suggested first algorithm for fast evaluation of the constant  π based on the AGM-method of Gauss (see, for example, [13], [14]). Using also the ascending transformations of Landen [39], Brent [11] suggested the first AGM-algorithms for evaluation of elementary transcendental functions. Later many authors have been going on to study and use the AGM-algorithms. Among those authors were the brothers Jonathan Borwein and Peter Borwein, who wrote the book ‘The Pi and the AGM’ [9], where the greatest number of AGM-algorithms were collected. Apart from the algorithms of calculation of elementary transcendental functions, in this book there were also algorithms for evaluation of some higher transcendental functions (the Euler Gamma function,for example). To compute such functions with accuracy up to  n  digits using the algorithms described in the book one needs

operations.

        About some other results connected with ‘Divide and Conquer’ and fast calculations see [1], [2], [3], [6], [7], [17], [18], [36], [41].

II. THE FEE METHOD

        An algorithm of computation of a function  f = f(x), is said to be fast, if for this algorithm

where  c  is a constant. Here and below we assume that for  M(n)  the Schönhage-Strassen bound holds. It is obvious that for any algorithm and any function  f,  the inequality

is valid. (Note that recording some number with accuracy up to n digits requires itself not less than  n + 1  operations.) Therefore, for fast algorithms

for any  ε > 0  and  n > n₁(ε).  That is, for the fast computational algorithms the order of upper bound of  S_f(n)  in  n,   n → ∞,  is correct.

        The method FEE (since 1990) [23]-[35] (see also [4]-[6], [40]) is at present the second known method (after the AGM) for fast evaluation of classical constants  e  and  π,  and elementary transcendental functions. But, unlike the AGM, the FEE is also the method for fast computation of higher transcendental functions. At present the FEE is the unique method, permitting to calculate fast such higher transcendental functions as the Euler Gamma function, hypergeometric, spherical, cylindrical etc. functions for algebraic values of the argument and parameters, the Riemann zeta function for integer values of the argument and the Hurwitz zeta function for integer values of the argument and algebraic values of the parameter.

2. Calculation of the constant  e

        The main idea of the method FEE is explained in the easiest way by the example of calculating the classical constant  e.  To begin with, we consider the algorithm of computation of  n!  in  log n  steps with the complexity

O(n log³ n log log n).

For simplicity we assume that  n = 2^k,   k ≥ 1.

Step 1. Calculate  n/2  products of the form:

a₁(1) = n(n–1),   a₂(1) = (n–2)(n–3) , ... , a_n/2(1) = 2*1;

Step 2. Calculate  n/4  products of the form:

a₁(2) = a₁(1)a₂(1),   a₂(2) = a₃(1)a₄(1), ... , a_n/4(2) = a_n/2(1)a_n/2-1(1),

... etc.

Step k, the last one. Calculate one product of the form:

a₁(k) = a₁(k–1)a₂(k–1),

This gives the result:  n!

        For the evaluation of the constant  e  take  m = 2^k,   k ≥ 1,  terms of the Taylor series for  e,

e = 1 + 1/1! + 1/2! + ... + 1/(m–1)! + R_m.

        Here we choose  m,  requiring that for the remainder  R_m  the inequality  R_m ≤ 2^–n–1   is fulfilled. This is the case, for example, when  m ≥ 4n/log n.  Thus, we take  m = 2^k  such that the natural number  k  is determined by the inequalities:  2^k ≥ 4n/log n > 2 ^k–1.

        We calculate the sum

S = 1 + 1/1! + 1/2! + ... + 1/(m–1)! =

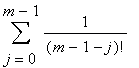
in  k  steps of the following process.

Step1. Combining in  S  the summands sequentially in pairs we carry out of the brackets the ‘obvious’ common factor and obtain

S = (1/(m – 1)! + 1/(m – 2)!) + (1/(m – 3)! + 1/(m – 4)!) + ... = (1/(m – 1)!)(1 + m – 1) + (1/(m – 3)!)(1+m – 3) + ...

We shall compute only integer values of the expressions in the parentheses, that is the values

m,  m – 2,  m – 4, ... .

Thus, at the first step the sum  S  is into

S = S(1);

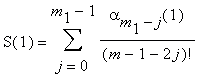
m₁ = m/2,  m = 2^k,  k ≥ 1.

At the first step  m/2  integers of the form

α_m1–j(1) = m – 2j,   j = 0, 1, ... ,  m₁ – 1.

are calculated. After that we act in a similar way: combining on each step the summands of the sum  S  sequentially in pairs, we take out of the brackets the ‘obvious’ common factor and compute only the integer values of the expressions in the brackets. Assume that the first  i  steps of this process are completed.

Step i+1  (i + 1 ≤k).

S = S(i+1);

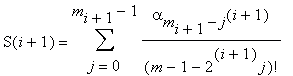
m_i+1 = m_i/2 = m/2ⁱ⁺¹, 

we compute only  m/2ⁱ⁺¹  integers of the form

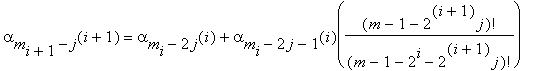
j = 0,  1, ... ,  m_i+1 – 1,  m = 2^k,  k ≥ i+1.  Here  ((m – 1 – 2ⁱ⁺¹j)!/(m – 1 – 2ⁱ – 2ⁱ⁺¹j)!)  is the product of  2ⁱ  integers.

...  etc.

Step k, the last one.  We compute one integer value  α₁(k),  we compute, using the fast algorithm described above the value  (m – 1)!,  and make one division of the integer  α₁(k)  by the integer  (m – 1)!,  with accuracy up to  n  digits. The obtained result is the sum  S,  or the constant  e  up to  n  digits. The complexity of all computations is

O(M(m) log² m) = O(M(n) log n).

        The method was called FEE (Fast E-function Evaluation) for the reason that it makes it possible to compute fast the Siegel E -functions, and in particular,  e^x.  A class of functions, which are ‘similar to the exponential function’ was given the name ‘E-functions’ by Siegel [49]. Among these functions are such higher transcendental functions as the hypergeometric function, cylindrical, spherical functions and so on. With the help of the FEE it is possible to compute fast any suitable power series. For example, for fast evaluation of the constant  π,  one can use the Euler formula

and apply the FEE to sum the Taylor series for

with the remainder terms  R₁,  R₂,  which satisfy the bounds

and for  r = n,  4( |R₁| + | R₁| ) < 2^–n.

To calculate  π  by the FEE it is possible to use also other approximations, for example from [5]. The complexity is

        To compute the Euler constant gamma with accuracy up to  n  digits, it is necessary to sum by the FEE two series. Namely, for  m = 6n,  k = n,   k ≥ 1,

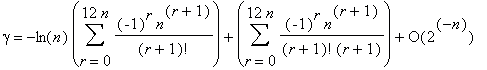
The complexity is

To evaluate fast the constant  γ  it is possible to apply the FEE to the approximation from [12].

        By the FEE the two following series are calculated fast:

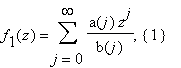
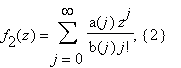
under the assumption that  a(j),  b(j)  are integers,  | a(j) | + | b(j) | ≤ (Cj)^K ;     | z | < 1;  K  and  C  are constants, and  z  is an algebraic number. The complexity of the evaluation of the series (1), (2) is

        Consider  y = f(x) = e^x.  We calculate the function  y = e^x  at the point  x = x₀  with accuracy  2^–n,  assuming first that

Take the integer  k,  satisfying the conditions  2^k–1 < n ≤ 2^k  and set  N = 2^k+1  (note that  2n ≤ N < 4n). For  x_N = α₃2^–3 + α₄2^–4 + ... + α_N2^–N,  where  α_j = 0  or  1,   j = 3, 4, ... , N,  we get

Then

Let us compute  e^x_N .  Represent  x_N  in the form

where

Here  β_ν  is a  2^ν–1 -digit integer, with  2 ≤ ν ≤ k + 1   and   k + 1 = log N.  Thus, it is possible to represent the number e^x_N  as the product

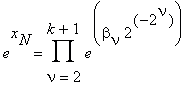
We expand each factor of this product in the Taylor series:

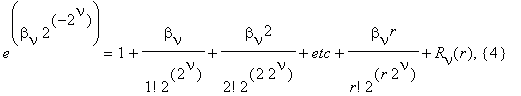
r = N 2^–ν+1 .

        For the remainder of the Taylor series  R_ν(r)  the following inequalities are valid:

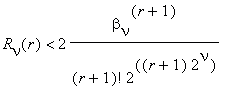
R_ν(r) < 2^–N .

Consequently, it is possible to rewrite (4) in the form

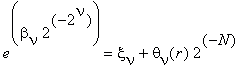
where

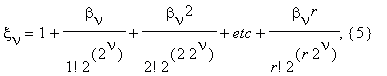
and the constants  θ_ν(r)  satisfy the estimate  0 < θ_ν(r) < 1 .

It is easy to see that the sum (5) is suitable for summing by means of the FEE. At the last step of the process we have in (5)

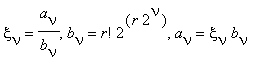
and then we make one division of the integer  a_ν  by the integer  b_ν  with accuracy up to  N  digits. That is, we obtain  η_ν  such that

Then  e^x_N  can be represented in the form

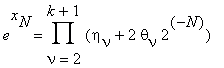
| θ_ν | ≤ 1 .

We define the integer  l  from the inequalities  2^l–1 < k ≤ 2^l.  Assuming that  η_ν = 1,  θ_ν = 0  for  ν > k,  we can rewrite the last relation in the form

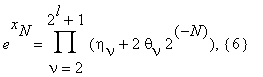
| θ_ν | ≤ 1 .

It is clear that  log k ≤ l < log k + 1. 

The last product is computed in  l  steps of the process, which is similar to calculating  n! .  We multiply the factors of (6) sequentially in pairs, computing at the first step  2^l–1  products of the form

(η_ν + 2 θ_ν 2^–N) (η_ν+1+ 2 θ_ν+1 2^–N) = η_νη_ν+1+ 2 θ_ν 2^–Nη_ν+1+ 2 θ_ν+12^–N η_ν + 4 θ_νθ_ν+12^–2N = η_ν,ν+1+ 8 θ_ν,ν+12^–N,

ν ≡ 0(2),  ν = 2, 3, ... , 2^l+ 1,
where  η_ν,ν+1  is the  N-digit integer such that

Here we take into account that  | η_ν | < e^x_N < e^x₀ < 3/2 .

After the 1-st step of this process the product (6) takes the form:

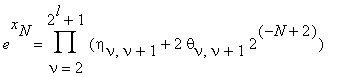
ν ≡ 0(2)
| θ_ν,ν+1 | ≤1 .
Further we act in a similar way.

After the 2-nd step of this process the product (6) takes the form:

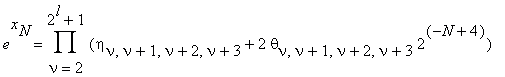
ν ≡ 2(4)
| θ_{ν,ν+1,ν+2,ν+3} | ≤ 1 .
... etc.

In  l  steps we obtain

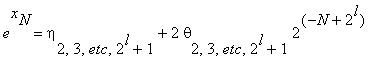
| θ_{2, ..., 2^l+1} | ≤ 1 .

Since  l < log k + 1,   k = log N – 1,   2n ≤ N < 4n,  we find from the last relation that

where  η = η_{2, ..., 2^l+ 1} ,   | θ | ≤ 1 .

The complexity of the computation of  e^x₀  with the help of this process is

Remark 1. We considered the case  0 < x₀ < 1/4 .  If  x₀ ≥ 1/4 ,  then we take the least integer  m  such that  m > 4x₀.  In this case  0 < x₀/m < 1/4 ,   e^x₀ = (e^x₀/m)^m .  Thus evaluation of  e^x₀  is reduced to evaluation of  e^x₀/m ,  0 <  x₀/m < 1/4 ,  and to taking the  m  -th power of the result. This doesn't make the bound worse, because  m  is a fixed number.

        Computation of the trigonometric functions  y = f(x) = sin x  and  y = f(x) = cos x  at the point x = x₀  can be reduced to the computation of real and imaginary parts of  e^ix₀.  We represent the number  x_N  in the same form as in the previous case, then  e^ix₀ = e^ix_N + 4θ₁2^–N ,

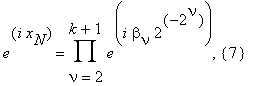
| θ_1^- | ≤ 1 .

We write

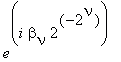
in the form

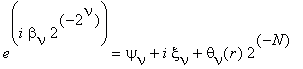
where

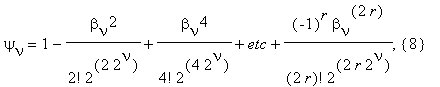
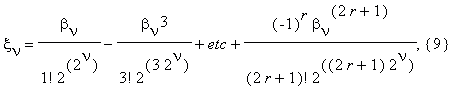
0 < θ_ν(r) < 1.

Then we perform with the sums (8), (9) the same actions as with the sum (4). Let  η_ν ,   f_ν  be  N -digit integers such that

,  

Then (7) can be represented in the form

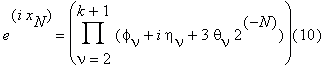
| θ_ν | ≤ 1 .

        We compute the product (10) by means of the process which is described in the previous paragraph. As a result we find with specially chosen  l,  N,  r 

whence

The complexity of the evaluation is the same as for the exponential function:

In [26] the following general theorem is proved:

Theorem. Let  y = f(x) be an elementary transcendental function, that is the exponential function, or a trigonometric function, or an elementary algebraic function, or their superposition, or their inverse, or a superposition of the inverses. Then

        The Euler gamma function  y = Γ(s),  is one of those higher transcendental functions, that, being not Siegel E-functions, at the same time can be calculated fast by the FEE. There are two algorithms for the evaluation of  Γ(s):  1) for rational values of the argument  s;  2) for algebraic values of the argument  s.  The first of these algorithms is more ‘simple’ than the second one. We compute the function  y = Γ(x) ,  for  x = x₀ = a/b ;   (a,b) = 1 ,  assuming at first that  0 < x₀ < 1 ,  that is   0 < a < b .  We use the representation of the gamma function in the form of the integral

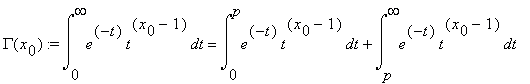
It is easy to see that for  p = n,  0 < x₀ < 1 ,

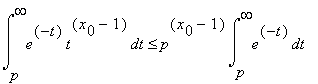
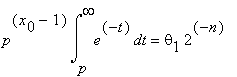,   0 < θ₁ < 3/4 .

Hence,

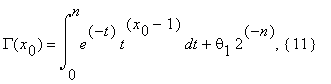
0 < θ₁ < 3/4.

Assuming that  r ≥ 3n ,  we expand the integrand in (11) in the Taylor series in powers of  t:

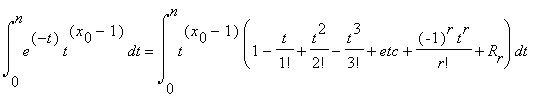
where  R_r = θ_r t^r+1/(r+1)! ,   | θ_r | ≤ 1 .  From here we have for  r+1 = 6n

where

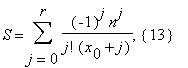
and we will calculate  Γ(x₀) = Γ(a/b)  by (12)-(13). We note, that for the calculation of the value  n^x₀ = n^a/b,   with accuracy up to  n  digits,  O(M(n))  operations are sufficient (by the Newton method). For the calculation of the sum  S  we take  r+1 = 2^k,   2^k–1 < 6n ≤ 2^k,  k ≥ 1;  terms of the series (13). We set

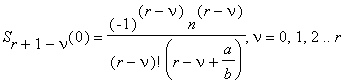
Then it is possible to rewrite (13) in the form

We compute the sum  S  by the FEE in  k  steps, combining at each step the summands of  S  sequentially in pairs and taking out of the brackets the ‘obvious’ common factor. However, unlike the computation of the constant  e  now in each pair of the brackets there are fractions, not integers. So that at each step we calculate the integer numerator and the integer denominator of the fraction, sitting in each pair of brackets (we do not divide until the last step). At the first step we have

At the 1-st step we calculate the integers

At the  j-th step (j ≤ k) we have

where  S_rj–ν(j) ;   ν = 0, 1, ... , r_j–1 ;  are defined by the equalities

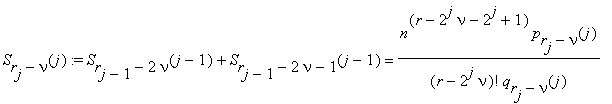
At the  j-th step (j ≤ k)  we calculate the integers

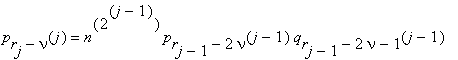
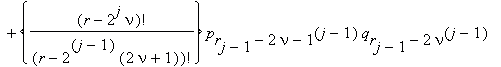
ν = 0, 1, ... , r_j–1 ;   r_j = (r + 1)/2^j .

... etc.

At the k-th (the last) step we calculate the integers  p_rk(k) = p₁(k) ,   q_rk(k) = q₁(k) ,   r!  and make one division with accuracy  2^–2n  by the formula

which gives the sum  S  with accuracy  2^–n–1 .  Hence  Γ(x₀) = Γ(a/b)  is calculated with accuracy  2^–n+1 ,   n ≥ 1 .  The complexity of such calculation is

Remark 2. We evaluated  Γ(x₀),    x₀ = a/b ,  assuming that  0 < x₀ < 1 .  If  x₀ ≥ 1 ,  then using the relation  Γ(x+1) = x Γ(x) ,  we reduce this calculation to the calculation at the point from the interval  (0, 1) .

        We shall evaluate  Γ(x₀) ,  where  x₀  is an algebraic number. As in Remark 2, we reduce this computation to the computation of  Γ(α) ,  0 < α < 1 ,  where  α  is an algebraic number. For simplicity, here we consider the case, where  α  is a real number of degree  μ ,   μ ≥ 2 .  We assume that we know  g(x) ,  the polynomial of the least degree with integer coefficients, whose root is  α,  that is

g_μ, g_μ–1, ..., g₀  are integers,  μ ≥ 2 .  As in the case of rational argument, we use (12), (13). We note that the computation of the value  n^α  with accuracy  2^–2n  by formula  n^α = e^α log n requires  O(M(n) log²n)  operations. The sum  S  from (12) takes the form

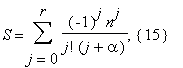
that is

where

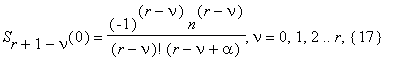
        The computation of  S  is realized in  k  steps,  r+1 = 2^k ,   2^k–1 < 6n ≤ 2^k ,   k ≥ 1 .  The peculiarity of this algorithm is that we use the main property of algebraic numbers to bound the growth of the computational complexity. Before the step  i,  where  i  is determined from the conditions  1 ≤ i ≤ k ,   2^i–1 < μ≤ 2ⁱ,  we perform with the sum (16), (17) the actions similar to the ones described above for the case of rational argument. However, arranging the terms of the sum (16) in groups in the same way as in the previous paragraph, what we calculate at each step now is not the numerator and the denominator of the fractions which are ‘in brackets’, but only the integer coefficients of the powers of  α,  of the polynomials in the numerators and denominators of the fractions ‘in brackets’.
At the  1-st step  in brackets there are the numbers

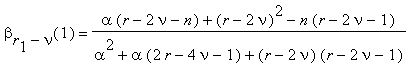
and we calculate the integers

ν = 0, 1, ... , (r+1)/2–1.

At  i-th step in brackets there are the numbers

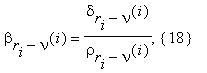
where

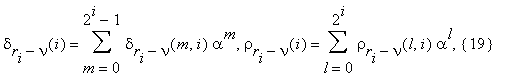
and we calculate the integers

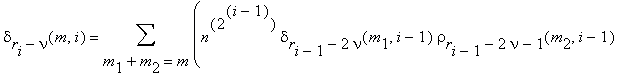
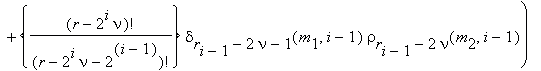
0 ≤ m₁ ≤ 2^i–1–1 ,   0 ≤ m₂ ≤ 2^i–1 .

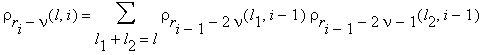
0 ≤ l₁ ≤ 2^i–1 ,   0 ≤ l₂ ≤ 2^i–1 .

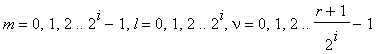
Note that the multiplication by the power of  α  and the computation of  δ  and  ρ ,  also the division of  δ  by  ρ ,   are not produced till the last step.

        Before the  i+1 -st step (1 ≤ i ≤k ,   2^i–1 < μ ≤ 2ⁱ) we reduce the polynomials (19) modulo polynomial  g(x)  for  x = α .  Thus, if

where  p_t–1 ,  ...,  p₀ ,  q_t ,  ...,  q₀  are integers,  t = 2ⁱ ,  then we divide  P(x)  and  Q(x) by  g(x)  with the remainders:

where  P₁(x)  and  Q₁(x)  are the polynomials with rational coefficients, and the degrees of the polynomials P₁(x)  and  Q₁(x)  are not greater than μ–1 .  From here and from (14) we obtain that

that is, in (18) we get

Multiplying, if necessary the numerator and the denominator of the fraction (20) by an integer common factor, we get in the numerator and the denominator of the fractions ‘in brackets’ the polynomials with integer coefficients of degree not higher than  μ–1 .  Starting with  i ,  at each step  i ,  i+1 ,  ... ,  k ,  we reduce the polynomials in  α ,  sitting in the numerator and the denominator of  β_ξ(j)  modulo  g(x) .  Since the coefficients of  g(x)  and the degree of  g(x)  are the absolute constants, we conclude that the values of these coefficients, participating in the reductions described above can increase in at most  g^μ  times, where

what does not make any influence on the bound of the complexity of the calculations we perform. At the last,  k -th, step of this process we get

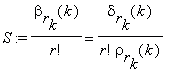
where

p, q ≤ μ–1 ,  and we calculate  δ_rk(k) ,   ρ_rk(k)  and  S,  and consequently  Γ(α)  with accuracy  2^–n+1.  The complexity of the computation

        The presented method FEE, the method of fast summation of series of a special form, permits to compute any elementary transcendental function for any value of the argument, the classical constants  e,  π,  the Euler constant  γ,  the Catalan and the Apery constants, such higher transcendental functions as the Euler gamma function and its derivatives, the hypergeometric, spherical, cylindrical and other functions for algebraic values of the argument and parameters, the Riemann zeta function for integer values of the argument and the Hurwitz zeta function for integer argument and algebraic values of the parameter, and also such special integrals as the integral of probability, the Fresnel integrals, the integral exponential function, the integral sine and cosine, and some other integrals for algebraic values of the argument with the complexity bound which is close to the optimal one, namely

At present, only the FEE makes it possible to calculate fast the values of the functions from the class of higher transcendental functions, certain special integrals of mathematical physics and such classical constants as Euler's, Catalan's and Apery's constants. An additional advantage of the method FEE is the possibility of parallelizing the algorithms based on the FEE.

III. ON THE COMPLEXITY OF COMPUTATIONS

        The concept of complexity of computation arose as a result of development of computational methods and information theory.

        Among the first investigations in the field of information theory were the works of Harry Nyquist [42] and Ralph Hartley [19], where the concept of the measure of information was introduced.

        We considered above the bit complexity, that defines the measure of efficiency of real calculations in the most sharp way. At the same time, for different problems it is possible to define the measure of efficiency of computations in different ways. Thus along with the bit complexity, there are also the algebraic, Boolean, Kolmogorov, rational etc. complexities. Some of them are determined by the amount of the bit, algebraic, etc. operations spent for the calculation; the others—by the number of steps of the computational process, for example, by the number of steps of work of the Turing machine.

        The first algorithm that was analyzed from the viewpoint of its complexity, was, it seems, the Euclidean algorithm for computing the greatest common divisor of two integers. Its complexity was measured by the total number of steps-divisions in this algorithm. The bounds for complexity of the Euclidean algorithm were obtained [48] by Antoine-André-Louis Reynaud (a rough estimate of the total number of steps of the algorithm, 1811), Pierre-Joseph-Étienne Finck (an estimate of the number of steps of the algorithm, close to the optimal one, 1841) and Gabriel Lamé (the optimal estimate, 1844). The last result is known in the literature as the Lamé theorem.

        Constructing algorithms of evaluation for a broad class of functions with the bit complexity bound which is close to the optimal one, and also obtaining non-trivial lower bounds of the bit complexity, are the main problems in the field which is called fast algorithms or fast computations. At present, there are many unsolved problems in this field, such as
– obtaining a nontrivial lower bound for the complexity of multiplication or for the complexity of evaluation of a transcendental function;
– constructing fast algorithms for computation of a higher transcendental function at transcendental points;
– constructing fast algorithms for calculation of such constants as the Brun constant; the values of the Riemann zeta function at non-integral points, etc.

        These and many other problems in the field of fast computations are still waiting for their solutions.

References

[1] V.B.Alekseev, From the Karatsuba Method for Fast Multiplication of Numbers to Fast Algorithms for Discrete Functions. Proceddings of the Steklov Inst.of Math., v.218, pp.15-22 (1997).

[2] V.B.Alekseev, S.A.Lozkin, Elements of graph theory, circuits and automata. Publ. VMK MGU, 58 pp., Moscow (2000).

[3] G.N.Arkhipov, V.N. Chubarikov, V.A. Sadovnichii, Lectures in Mathematical Analysis. Publ. ‘Vysshaya Shkola’, 695 pp., Moscow (1999).

[4] E.Bach, The complexity of number-theoretic constants. Info.Proc.Letters, N 62, pp.145-152 (1997).

[5] D.H.Bailey, P.B.Borwein and S.Plouffe, On the rapid computation of various polylogarithmic constants. Math. Comp., v.66, pp.903-913 (1997).

[6] J.C.Bajard, J.M.Muller, Calcul et arithmetique des ordinateurs. Hermes Science, 226 pp. (2004).

[7] L.A.Bassalygo, Note on fast multiplication of polynomials over Galois fields. Probl. of Inform.Transm., 14 (1), pp.71-72 (1978).

[8] Benderskij Yu.V., Fast Computations. Dokl.Akad.Nauk SSSR, v.223, N 5, pp.1041-1043 (1975).

[9] J.M.Borwein and P.B.Borwein, Pi and the AGM. Wiley, 414 pp., New York (1987).

[10] J.M.Borwein, D.M.Bradley and R.E.Crandall, Computational strategies for the Riemann zeta function. J. of Comput. Appl. Math., v.121, N 1-2, pp.247-296 (2000).

[11] R.P.Brent, Fast Multiple-Precision Evaluation of Elementary Functions. ACM, v.23, N 2, pp.242-251 (1976).

[12] R.P.Brent and E.M.McMillan, Some new algorithms for high-precision computation of Euler's constant. Math. Comp., v.34, pp.305-312 (1980).

[13] B.C.Carlson, Algorithms involving arithmetic and geometric means. Amer. Math. Monthly, v.78, pp.496-505 (1971).

[14] B.C.Carlson, An algorithm for computing logarithms and arctangents. Math.Comp., v.26, pp.543-549 (1972).

[15] S.A.Cook, On the minimum computation time of functions. Thesis, Harvard University (1966).

[16] D.Coppersmith and S.Winograd, On the asymptotic complexity of matrix multiplication. SIAM Journal on Computing, v.11, N 3, pp.472-492 (1982).

[17] S.B.Gashkov, On the Complexity of Integration of Rational Fractions. Proceedings of the Steklov Inst.of Math., v.218, pp.122-133 (1997).

[18] S.B.Gashkov, V.N. Chubarikov, Arithmetics. Algorithms. The Complexity of Computations. Publ. ‘Vysshaya Shkola’, 2-d ed., 320 pp., Moscow (2000).

[19] R.V.L.Hartley, Transmission of Information. Bell System Technical Journal, v.7, pp.535-563 (1928).

[20] Karatsuba A. and Ofman Yu., Multiplication of Multiplace Numbers on Automata. Dokl.Akad.Nauk SSSR, v.145, N 2, pp.293-294 (1962).

[21] A.Karacuba, Berechnungen und die Kompliziertheit von Beziehungen. EIK, N 11, pp.10-12 (1975).

[22] A.A.Karatsuba, The Complexity of Computations. Proceedings of the Steklov Institute of Mathematics, v.211, pp.169-183 (1995).

[23] Karatsuba E.A., Fast computation of exp(x). Problems of Information Transmission, v.26, N 3, p.109, Chronicle-17th All-Union School on Theory of Information and its Applications (1990).

[24] Karatsuba E.A., On a new method for fast evaluation of transcendental functions. Uspechi Mat. Nauk, v.46, N 2 (278), pp.219-220 (1991).

[25] Karatsuba E.A., On the fast computation of transcendental functions. Doklady Akad. Nauk SSSR, v.319, N 2, pp.278-279 (1991).

[26] Karatsuba E.A., Fast evaluations of transcendental functions. Probl. Peredachi Informat., v.27, N 4, pp.87-110 (1991).

[27] Karatsuba E.A., Fast evaluation of  ζ(3).  Probl. Peredachi Informat., v.29, N 1, pp. 68-73 (1993).

[28] Catherine A.Karatsuba, Fast evaluation of Bessel functions. Integral Transforms and Special Functions, v.1, N 4, pp.269-276 (1993).

[29] Karatsuba E.A., Fast Evaluation of Riemann zeta-function  ζ(s)  for integer values of argument  s.  Probl. Peredachi Informat., v.31, N 4, pp.69-80 (1995).

[30] Karatsuba E.A., On fast computation of Riemann zeta-function for integer values of argument. Doklady RAS, v.349, N 4, p.463 (1996).

[31] Karatsuba E.A., Fast evaluation of Hurwitz zeta function and Dirichlet L -series, Problem. Peredachi Informat., v.34, N 4, pp.342-353 (1998).

[32] Ekatharine A. Karatsuba, Fast evaluation of hypergeometric function by FEE. Computational Methods and Function Theory (CMFT'97), N.Papamichael, St.Ruscheweyh and E.B.Saff, eds., World Sc.Pub., pp.303-314 (1999).

[33] E.A.Karatsuba, On the computation of the Euler constant gamma. University of Helsinki preprint, 21 pp. (1999); J. of Numerical Algorithms, v.24, pp.83-97 (2000).

[34] E.A.Karatsuba, Fast computation of  ζ(3)  and of some special integrals, using the polylogarithms, the Ramanujan formula and it's generalization. J. of Numerical Mathematics BIT, v. 41, N 4, pp.722-730 (2001).

[35] E.A.Karatsuba, Fast computation of some special integrals of mathematical physics. Scientific Computing, Validated Numerics, Interval Methods, W.Kramer,J.W.von Gudenberg,eds., pp.29-41 (2001).

[36] D.E.Knuth, The art of computer programming. v.2 Addison-Wesley Publ.Co., 724 pp., Reading (1969).

[37] A.N.Kolmogorov, Asymptotic characteristics of some completely bounded metric spaces. Dokl. Akad. Nauk SSSR, v.108, N 3, pp.385-388 (1956).

[38] A.N. Kolmogorov, Information Theory and the Theory of Algorithms. Publ. Nauka, 303 pp., Moscow (1987).

[39] J.Landen, An investigation of a general theorem for finding the length of any arc of any conic hyperbola, by means of two elliptic arcs, with some other new and useful theorems deduced therefrom. Philos.Trans.Royal Soc. London, v.65, pp.283-289 (1775).

[40] D.W.Lozier and F.W.J.Olver, Numerical Evaluation of Special Functions. Mathematics of Computation 1943-1993: A Half -Century of Computational Mathematics, W.Gautschi,eds., Proc. Sympos. Applied Mathematics, AMS, v.48, pp.79-125 (1994).

[41] V.I.Nechaev, Elements of Cryptography. Basic Protection Information Theory. Publ. ‘Vysshaya Shkola’, 110 pp., Moscow (1999).

[42] H. Nyquist, Certain factors affecting telegraph speed. Bell System Technical Journal, v. 3, pp. 324-346 (1924). [43] V.Ya.Pan, Strassen's algorithm is not optimal. Proc. ACM Symp. on the Found. of Comp.Science, pp.166-176 (1978).

[44] E.Salamin, Computation of  π  using arithmetic-geometric mean. Math. Comp., v.30, N 135, pp.565-570 (1976).

[45] A.Schönhage, Schnelle Multiplikation grosser Zahlen. Computing, v.1, pp.182-196 (1966).

[46] A.Schönhage und V.Strassen, Schnelle Multiplikation grosser Zahlen. Computing, v.7, pp.281-292 (1971).

[47] A. Schönhage, A. F. W. Grotefeld and E. Vetter, Fast Algorithms — A Multitape Turing Machine Implementation. BI-Wiss.-Verl., 300 pp., Zürich (1994).

[48] J. Shallit, Origins of the Analysis of the Euclidean Algorithm. Historia Mathematica, v.21, pp.401-419 (1994).

[49] C.L.Siegel, Transcendental numbers. Princeton University Press, 102 pp., Princeton (1949).

[50] V.Strassen, Gaussian elimination is not optimal. J. Numer. Math., N 13, pp.354-356 (1969).

[51] A.L.Toom, The complexity of a scheme of functional elements realising the multiplication of integers. Dokl.Akad.Nauk SSSR, v.150, N 3, pp.496-498 (1963).

Answers to the frequently asked questions

        About the FEE see E.A.Karatsuba's paper:
‘Fast evaluation of Hurwitz zeta function and Dirichlet L-series’.
Problem. Peredachi Informat., v.34, N 4, pp.342-353 (1998).

• in MS-Word format (220 672 bytes);
• HTML (431 870 bytes) (It need to download the Vector Graphic Rendering component);