Область вычислительной математики, которая называется быстрые алгоритмы, появилась в 1960 году.
Под алгоритмом мы будем понимать правило или способ вычисления, не формализуя это понятие. Далее будем считать, что числа записаны в двоичной системе счисления, знаки которой 0 и 1 называются битами.
Опр. 1. Запись знаков 0, 1 , плюс, минус, скобка; сложение, вычитание и умножение двух битов назовём одной элементарной или битовой операцией.
Быстрые алгоритмы — это область вычислительной математики, которая изучает алгоритмы вычисления заданной функции с заданной точностью с использованием как можно меньшего числа битовых операций. Тем самым, алгоритмы, которые можно назвать быстрыми, являются реальными алгоритмами. Такие алгоритмы, реализованные на ЭВМ в программном (а иногда и аппаратном) обеспечении позволяют существенно увеличить производительность работы компьютера, а иногда и решить задачи, размер которых не позволял найти решение путём применения обычных методов вычисления. Вопрос о размере задачи, которую можно решить за некоторое время с помощью данного компьютера, приводит нас к понятию сложности вычисления.
В дальнейшем, если не оговаривается иначе, под сложностью вычисления подразумевается битовая сложность.
Первые постановки задач о сложности вычислений (1956 г.) принадлежат А. Н. Колмогорову [37], [38], который в то же время подчёркивал, что «цикл моих работ по теории информации был создан под большим влиянием публикаций Норберта Винера и Клода Шеннона».
Прежде чем ввести понятие сложности вычисления, определим, что значит вычислить функцию в заданной точке. Рассмотрим наиболее простой пример вычисления вещественной функции y = f(x) вещественного переменного x, a ≤ x ≤ b. Пусть f(x) на (a,b) удовлетворяет условию Липшица порядка α, 0 < α <1, так что при x1, x2 ∊ (a,b):
|f(x1) – f(x2)| ≤ |x1 – x2|α.
Пусть n — натуральное число.
Опр. 2. Вычислить функцию y = f(x) в точке x = x0 ∊ (a,b) с точностью до n знаков, значит найти число A, что
|f(x0) – A| ≤ 2–n.
Опр. 3. Количество битовых операций, достаточное для вычисления функции f(x) в точке x = x0 с точностью до n знаков посредством данного алгоритма, называется сложностью вычисления f(x) в точке x = x0.
Таким образом, сложность вычисления f(x) в точке x = x0 есть функция n; а также f(x) и x = x0. Эту функцию обозначают символом
Ясно, что Sf зависит также от алгоритма вычисления и при разных алгоритмах будет разной. Сложность вычисления непосредственно связана со временем, затрачиваемым компьютером на это вычисление и потому иногда в литературе обозначается «временной» функцией T(n) [36].
Вопрос о поведении Sf(n) при n → ∞ для класса функций или конкретной функции f, был впервые поставлен А. Н. Колмогоровым около 1956 года. Поскольку при вычислениях в первую очередь используются четыре арифметических действия: сложение, вычитание, умножение и деление, то прежде всего нужно знать количество битовых операций, достаточное для выполнения этих действий. Из определений 2 и 3 следует, что числа x0 и A можно представить в виде целой части и n двоичных знаков после запятой, т.е.
где νj, μj = 0 или 1, j = 1, 2, ... , n.
Так как целые части [A], [x0] — фиксированные величины, а n → ∞, то действия производятся по существу с n-значными числами. Отсюда прежде всего возникает вопрос о сложности вычисления суммы, разности, произведения и частного двух n-значных чисел a и b. Заметим, что деление (с остатком) сводится к сложению, вычитанию и умножению чисел.
Для записи чисел a и b требуется по меньшей мере 2n битовых операций. Следовательно, сложность сложения (вычитания) a и b не меньше 3n битовых операций, и не больше (если делать это обычным способом), чем 4n битовых операций. Таким образом, порядок количества битовых операций, необходимых и достаточных для выполнения сложения (вычитания), один и тот же.
В дальнейшем для краткости, будем называть «битовые операции» просто «операциями». Следующим вопросом является вопрос о количестве операций, достаточных для вычисления произведения ab, или о сложности умножения. Функция сложности умножения получила специальное обозначение M(n).
Перемножая два n-значных числа обычным школьным способом «в столбик», мы при этом фактически складываем n n-значных чисел. Так что для сложности этого «школьного» или «обычного» метода мы имеем оценку сверху M(n) = O(n2).
В 1956 г. А. Н. Колмогоров высказал гипотезу, что нижняя оценка M(n) при любом методе умножения есть также величина порядка n2 (так называемая «гипотеза n2 Колмогорова»). На правдоподобность «гипотезы n2» указывал тот факт, что метод умножения «в столбик» известен не менее 4-х тысячелетий (например, этим методом пользовались шумеры), и если бы был более быстрый метод умножения, то он, вероятно, уже был бы найден.
В 1960 А. А. Карацуба [20], [21], [22] (см. также [36]) нашёл новый метод умножения двух n-значных чисел с оценкой сложности
и тем самым опроверг «гипотезу n2». Этот метод впоследствии был назван «Divide and Conquer» («Разделяй и властвуй»); другие, используемые в настоящее время названия этого метода — «Binary Splitting», «Принцип Дихотомии» и т. п.
С момента появления «Divide and Conquer» начала развиваться теория быстрых вычислений. Исследования с целью поиска алгоритма умножения со сложностью, близкой к оптимальной, были продолжены рядом авторов (среди них были Тоом [51], Кук [15], Шёнхаге [45]), и в 1971 г. Шёнхаге и Штрассен [46], [47] построили алгоритм с наилучшей на настоящее время оценкой для M(n),
При построении этого алгоритма кроме "Divide and Conquer" они использовали идею выполнения арифметических действий по модулю чисел Ферма 22n+ 1, а также быстрое преобразование Фурье.
На основе «Divide and Conquer» были построены алгоритмы быстрого умножения матриц. Первый такой алгоритм в 1970 г. нашёл Штрассен [50], в дальнейшем эти исследования были продолжены Коперсмитом, Виноградом [16], Паном [43] и др.
Приблизительно в это же время стали появляться и первые быстрые алгоритмы для вычисления элементарных алгебраическх функций. Как уже упоминалось выше, деление числа a на число b с остатком, т. е. вычисление чисел q и r в формуле
сводится к сложению, вычитанию и умножению, и если a и b являются n-значными числами, то сложность деления O(M(n)).
Самый простой алгоритм деления заключается в вычислении методом Ньютона обратной величины 1/b с точностью до n знаков с последующим умножением на a по алгоритму быстрого умножения.
Пусть надо вычислить x = 1/b, где 1/2 ≤ b ≤ 1 (если это не так, то умножая или деля b на 2N получим выполнение указанного условия). Возьмём в качестве начального приближения x0 = 3/2 и вычисляем по формуле
Этот метод обеспечивает достаточно быструю сходимость к 1/b, поскольку из равенства xn = 1/b – ε, следует, что xn+1 = 1/b – bε2.
Для извлечения корня k-ой степени из числа, т. е. для вычисления a1/k можно также воспользоваться методом Ньютона. Пусть k ≥ 2 — целое число и надо вычислить x = a1/k, где a ≥ (k + 1)k. Вычисляем x по формуле:
Заметим, что умножением или делением на 2kN можно всегда добиться выполнения для a условия a ≥ (k + 1)k (иногда это условие оказывается лишним, т. е. указанный процесс быстро сходится и при других a).
За начальное приближение можно взять, например, одно из двух чисел d или d+1, где d — целое число, удовлетворяющее условию dk < a ≤ (d + 1)k. Тогда одно из чисел |d – z1/k| или |d + 1 – z1/k| не превосходит 1/2.
Сложность вычисления этим методом будет O(M(n)).
Первые быстрые алгоритмы для вычисления элементарных алгебраических функций, основанные на методе Ньютона, появились в работах Кука [15], Бендерского [8] и Брента [11] (см. также [36]).
Используя метод Ньютона можно доказать следующую теорему [11]:
Теорема. Если уравнение f(x) = 0 имеет простой корень ζ ≠ 0, f(x) непрерывна по Липшицу в окрестности ζ, и мы можем вычислить f(x) с точностью до n знаков за O(M(n)j(n)) операций, где j(n) — положительная, монотонно возрастающая функция, для любого x из окрестности ζ, то ζ можно вычислить с точностью до n знаков также за O(M(n)j(n)) операций.
В 1976 г. Саламин [44] и Брент [11] предложили первый алгоритм быстрого вычисления константы π, основанный на АГС-методе Гаусса (см., например, [13], [14]). Используя также восходящие преобразования Ландена [39], Брент [11] предложил первые АГС-алгоритмы для быстрого вычисления простейших трансцендентных функций. В дальнейшем исследование и использование АГС-алгоритмов было продолжено многими авторами, среди которых были братья Джонатан и Питер Борвайны,написавшие книгу «The Pi and the AGM» («Пи и АГС») [9], где собрано наибольшее число АГС-алгоритмов. Кроме алгоритмов вычисления простейших трансцендентных функций, в этой книге содержатся также алгоритмы для вычисления некоторых высших трансцендентных функций (гамма-функции Эйлера, например). Чтобы вычислить такие функции с точностью до n знаков с помощью описанных в книге алгоритмов требуется
операций.
О других результатах, связанных с «Divide and Conquer» и быстрыми вычислениями, см. [1], [2], [3], [6], [7], [17], [18], [36], [41].
Будем называть «быстрым» такой алгоритм вычисления функции f = f(x), что для этого алгоритма
где c есть константа. Здесь и далее предполагаем, что для M(n) справедлива оценка Шёнхаге-Штрассена. Ясно, что для любого алгоритма и любой функции f, выполняется неравенство:
(Заметим, что только запись числа с точностью до n знаков требует не меньше, чем n + 1 операций.) Следовательно, для быстрого алгоритма
для любого ε > 0 и n > n1(ε). Тем самым, быстрым алгоритмам соответствует правильный порядок оценки сверху Sf(n) по n, n → ∞.
Метод БВЕ (от 1990) [23]-[35] (см. также [4]-[6], [40]) является вторым после метода АГС известным на настоящее время методом быстрого вычисления классических констант e и π, и простейших трансцендентных функций. Но, в отличие от АГС, метод БВЕ является также методом быстрого вычисления высших трансцендентных функций. В настоящее время БВЕ является единственным методом, позволяющим вычислить быстро такие высшие трансцендентные функции, как гамма-функцию Эйлера, гипергеометрические функции, цилиндрические, сферические и т. д. функции при алгебраических значениях аргумента и параметров, дзета-функцию Римана и дзета-функцию Гурвица при целых значениях аргумента и алгебраических значениях параметра.
Основная идея метода БВЕ проще всего объясняется на примере вычисления классической постоянной e. Рассмотрим сначала алгоритм вычисления n! за log n шагов со сложностью O(n log3 n log log n). Для простоты мы предполагаем, что n = 2k, k ≥ 1.
1-й шаг. Вычисляются n/2 произведений вида:
2-й шаг. Вычисляются n/4 произведений вида:
... и так далее.
k-й, последний шаг. Вычисляется одно произведение:
и это даёт результат: n!
Для вычисления константы e возьмём m = 2k, k ≥ 1, членов ряда Тейлора для e,
При этом выбираем m так, чтобы для остатка Rm выполнялось неравенство Rm ≤ 2–n–1 . Это будет, например, когда m ≥ 4n / log n. Таким образом, возьмем m = 2k таким, что натуральное число k определяется неравенствами: 2k ≥ 4n / log n > 2 k–1.
Будем вычислять сумму
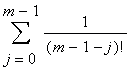
за k шагов следующего процесса.
1-й шаг. Объединяя слагаемые S последовательно попарно и вынося за скобки «очевидный» общий множитель, получаем
Будем вычислять только целые значения выражений, стоящих в скобках, т. е. значения m, m – 2, m – 4, ... . Таким образом, на первом шаге сумма S преобразуется к виду
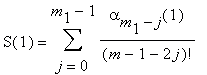
m1 = m / 2, m = 2k, k ≥ 1. На первом шаге вычисляются m / 2 целых чисел вида
Далее мы действуем аналогично: объединяя на каждом шаге слагаемые суммы S последовательно попарно, мы выносим за скобки «очевидный» общий множитель и вычисляем только целые значения выражений в скобках. Пусть сделано i шагов такого процесса.
i+1 -й (i + 1 ≤k) шаг.
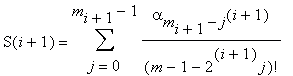
mi+1 = mi / 2 = m / 2i+1, вычисляем только m / 2i+1 целых чисел вида
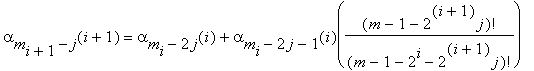
j = 0, 1, ... , mi+1 – 1, m = 2k, k ≥ i+1. Здесь ((m – 1 – 2i+1j)! / (m – 1 – 2i – 2i+1j)!) есть произведение 2i целых чисел.
... и так далее.
Последний, k-й шаг. Вычисляем одно целое α1(k), вычисляем, пользуясь вышеописанным быстрым алгоритмом, значение (m – 1)!, и производим одно деление целого числа α1(k) на число (m – 1)! с точностью до n знаков. Получившийся результат и есть сумма S, или константа e с точностью до 2–n. Сложность всех вычислений есть
Метод получил название «БВЕ» (Быстрое Вычисление E-функций) потому, что даёт возможность вычислять быстро E-функции Зигеля, и в частности, ex.
Зигель [49] назвал «E-функциями» класс функций, «похожих на экспоненциальную». К ним принадлежат такие высшие трансцендентные функции как гипергеометрические, сферические, цилиндрические функции и т. д.
С помощью БВЕ можно вычислить быстро любой подходящий степенной ряд. Например, для быстрого вычисления константы π, можно воспользоваться формулой Эйлера
а метод БВЕ применить к суммированию рядов Тейлора для
с остаточными членами R1, R2, для которых справедливы оценки
и при r = n, 4( |R1| + | R1| ) < 2–n. Чтобы вычислить π с помощью БВЕ можно воспользоваться также и другими приближениями, например из [5].
Чтобы вычислить постоянную Эйлера гамма с точностью до n знаков, нужно просуммировать с помощью БВЕ два ряда. А именно, при m = 6n, k = n, k ≥ 1,
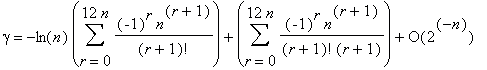
При этом
Для быстрого вычисления константы γ можно также применить метод БВЕ к приближению из [12].
С помощью БВЕ можно вычислить быстро следующие два вида рядов:
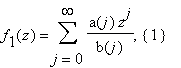
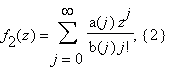
при условии, что a(j), b(j) — целые числа, | a(j) | + | b(j) | ≤ (Cj)K ; | z | < 1; K и C есть константы, и z есть алгебраическое число. Сложность вычисления рядов (1), (2) с точностью до n знаков есть
Пусть y = f(x) = ex. Вычислим функцию y = ex в точке x = x0 с точностью 2–n , предполагая сначала, что
Возьмём целое число k, удовлетворяющее условиям 2k–1 < n ≤ 2k и положим N = 2k+1 (заметим, что 2n ≤ N < 4n). Пусть xN = α32–3 + α42–4 + ... + αN2–N, где αj = 0 или 1, j = 3, 4, ... , N, и
Тогда
Будем вычислять exN . Представим xN в виде
где
Здесь βν есть 2ν–1-значное целое число, причём 2 ≤ ν ≤ k + 1 и k + 1 = log N. Таким образом, число exN можно представить в виде произведения
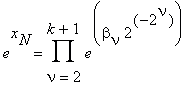
Разложим каждый множитель этого произведения в ряд Тейлора:
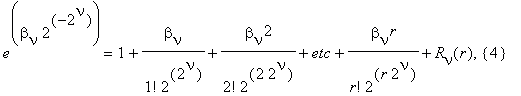
r = N 2–ν+1 .
Для остаточного члена ряда Rν(r) справедливо следующее неравенство:
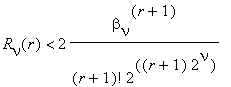
Отсюда Rν(r) < 2–N .
Следовательно, (4) можно записать в виде
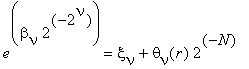
где
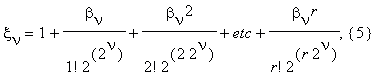
и постоянные θν(r), 0 < θν(r) < 1 . Легко видеть, что сумма (5) является подходящей для её суммирования с помощью БВЕ. На последнем шаге процесса в (5) имеем
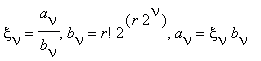
а затем производим деление целого числа aν на целое bν с точностью до N знаков. Тем самым, получаем такое ην, что
Следовательно exN может быть представлено в виде
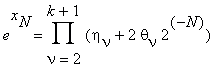
| θν | ≤ 1 .
Определим целое число l неравенствами 2l–1 < k ≤ 2l. Предполагая, что ην = 1, θν = 0 для ν > k, мы можем записать последнее выражение в виде
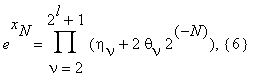
| θν | ≤ 1 .
Ясно, что log k ≤ l < log k + 1. Последнее произведение вычисляется за l шагов процесса, который аналогичен вычислению n! . Перемножим множители (6) последовательно попарно, вычисляя на 1-ом шаге 2l–1 произведений вида
(ην + 2 θν 2–N) (ην+1+ 2 θν+1 2–N) = ηνην+1+ 2 θν 2–Nην+1+ 2 θν+12–N ην + 4 θνθν+12–2N = ην,ν+1+ 8 θν,ν+12–N,
ν ≡ 0(2), ν = 2, 3, ... , 2l+ 1,
где ην,ν+1 есть N-значное число, такое что
Здесь мы учитываем, что | ην | < exN < ex0 < 3/2 .
После 1-го шага такого процесса произведение (6) принимает вид:
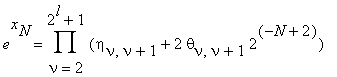
ν ≡ 0(2)
| θν,ν+1 | ≤1 .
Далее действуем аналогичным образом.
После 2-го шага такого процесса (6) принимает вид:
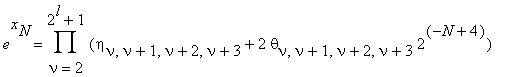
ν ≡ 2(4)
| θν,ν+1,ν+2,ν+3 | ≤ 1 .
... и так далее.
Через l шагов получим
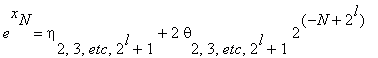
| θ2, ..., 2l+1 | ≤ 1 .
Поскольку l < log k + 1, k = log N – 1, 2n ≤ N < 4n, то из последнего соотношения находим
где η = η2, ..., 2l+ 1 , | θ | ≤ 1 .
Сложность вычисления ex0 с помощью такого процесса есть
Замечание 1. Мы рассмотрели случай 0 < x0 < 1/4 . Если x0 ≥ 1/4 , возьмём наименьшее целое число m , такое что m > 4x0. В этом случае 0 < x0/m < 1/4 , ex0 = (ex0/m)m . Тем самым вычисление ex0 сводится к вычислению ex0/m , 0 < x0/m < 1/4 , после чего результат возводится в степень m . Это не ухудшает оценку сложности вычисления, поскольку m есть фиксированное число.
Вычисление тригонометрических функций y = f(x) = sin x и y = f(x) = cos x в точке x = x0 может быть сведено к вычислению реальной и мнимой частей eix0. xN представим в том же виде, что и в предыдущем случае, при этом eix0 = eixN + 4θ12–N ,
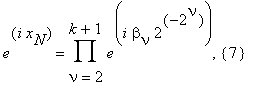
| θ1- | ≤ 1 .
Запишем
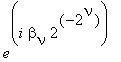
в виде
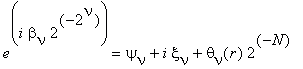
где
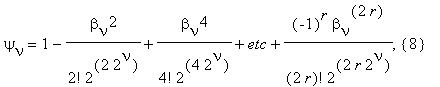
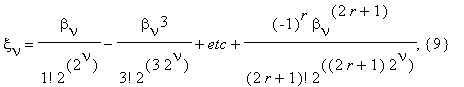
0 < θν(r) < 1. Далее мы производим с суммами (8), (9) те же действия, что и с суммой (4). Пусть ην , fν есть N-значные числа, такие что
Тогда (7) может быть представлено в виде
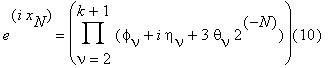
| θν | ≤ 1 .
Вычисляем произведение (10) посредством процесса, описанного в предыдущем параграфе. В результате со специально выбранными l, N, r находим
и отсюда
Сложность вычисления та же, что и для экспоненциальной функции:
В [26] доказана следующая общая теорема:
Теорема. Пусть
Гамма функция Эйлера y = Γ(s) относится к тем высшим трансцендентным функциям, которые не будучи E-функциями Зигеля, могут быть, тем не менее, быстро вычислены с помощью метода БВЕ. Есть два алгоритма для вычисления Γ(s): 1) для вычисления Γ(s) при рациональных значениях аргумента s; 2) для вычисления Γ(s) при алгебраических значениях s. Первый из этих алгоритмов является более «простым», чем второй. Вычислим функцию y = Γ(x) , при x = x0 = a/b ; (a,b) = 1 , предполагая сначала, что 0 < x0 < 1 , т. е. что 0 < a < b . Воспользуемся представлением гамма-функции в виде интеграла
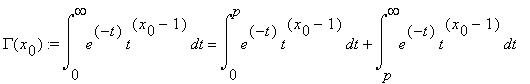
Легко видеть, что при p = n, 0 < x0 < 1 ,
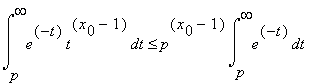
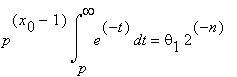 , 0 < θ1 < 3/4 .
, 0 < θ1 < 3/4 .Следовательно,
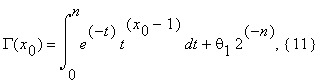
0 < θ1 < 3/4.
Предполагая, что r ≥ 3n , разложим подинтегральную функцию в (11) y = e–t , в ряд Тейлора по степеням t:
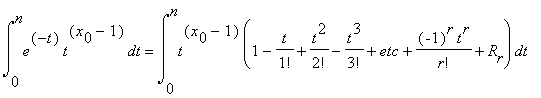
где Rr = θr tr+1/(r+1)! , | θr | ≤ 1 . Отсюда имеем при r+1 = 6n
где
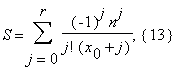
и мы будем вычислять Γ(x0) = Γ(a/b) по формулам (12)-(13). Заметим, что для вычисления nx0 = na/b, с точностью до n знаков достаточно O(M(n)) операций (методом Ньютона). Чтобы вычислить S возьмем r+1 = 2k, 2k–1 < 6n ≤ 2k, k ≥ 1; членов ряда (13). Пусть
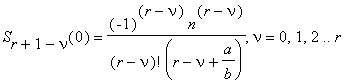
Тогда (13) можно записать в виде
Вычислим сумму S с помощью БВЕ за k шагов, объединяя на каждом шаге слагаемые S последовательно попарно и вынося за скобки «очевидный» общий множитель. Однако, в отличие от вычисления константы e методом БВЕ, теперь в скобках будут находиться не целые числа, а дроби. Поэтому теперь на каждом шаге будут вычисляться целый числитель и целый знаменатель дроби, стоящей в скобках (деление не производится до последнего шага). На первом шаге имеем
На 1-ом шаге вычисляем целые числа
На j-ом шаге (j ≤ k) имеем
где Srj–ν(j) ; ν = 0, 1, ... , rj–1 ; определяются равенствами
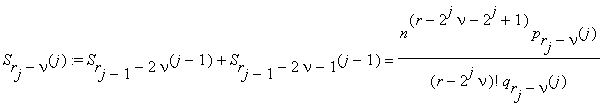
На j-ом шаге (j ≤ k) вычисляем целые числа
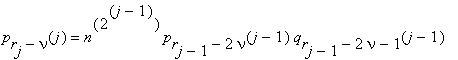
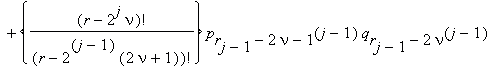
ν = 0, 1, ... , rj–1 ; rj = (r + 1) / 2j .
И так далее.
На k-ом (последнем) шаге вычисляем целые числа prk(k) = p1(k) , qrk(k) = q1(k) , r! и производим одно деление с точностью до 2–2n по формуле
что даёт сумму S с точностью 2–n–1 . Следовательно значение Γ(x0) = Γ(a/b) вычислено с точностью 2–n+1 , n ≥ 1 . Сложность такого вычисления есть
Замечание 2. Мы вычислили Γ(x0), x0 = a / b , предполагая, что 0 < x0 < 1 . Если x0 ≥ 1 , то, пользуясь соотношением, Γ(x+1) = x Γ(x) , сводим вычисление в нужной точке к вычислению в точке из интервала (0, 1) .
Вычислим Γ(x0) , при условии, что x0 есть алгебраическое число. В соответствии с Замечанием 2, сведём это вычисление к вычислению Γ(α) , 0 < α < 1 , где α есть алгебраическое число степени μ , μ ≥ 2 . Для простоты, рассмотрим случай, когда α является вещественным числом. Предполагается, что известен многочлен g(x) , наименьшей степени с целыми коэффициентами, корнем которого является число α , т. е.
gμ, gμ–1, ..., g0 — целые числа, μ ≥ 2 . Как и в случае рационального аргумента воспользуемся формулами (12), (13). Отметим, что вычисление nα с точностью 2–2n по формуле nα = eα log n требует O(M(n) log2n) операций. Сумма S из (12) принимает вид
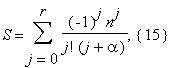
т. е.
где
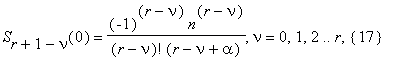
Вычисление S выполняется за k шагов, r+1 = 2k , 2k–1 < 6n ≤ 2k , k ≥ 1 . Особенностью этого алгоритма является использование основного свойства алгебраических чисел для ограничения роста сложности вычисления. До шага i , где i определяется условиями 1 ≤ i ≤ k , 2i–1 < μ≤ 2i , производим с суммой (16), (17) действия, аналогичные вышеописанным для случая рационального аргумента. Однако, группируя слагаемые суммы (16) таким же образом как и в предыдущем параграфе, теперь мы вычисляем на каждом шаге не числитель и знаменатель дробей, находящихся в скобках, а лишь целые коэффициенты при степенях α, многочленов, находящихся в числителе и знаменателе дробей «из скобок».
На 1-ом шаге в скобках находятся дроби
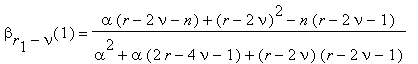
вычисляются числа
ν = 0, 1, ... , (r+1)/2–1.
На i-ом шаге в скобках находятся дроби
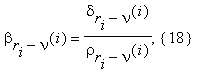
где
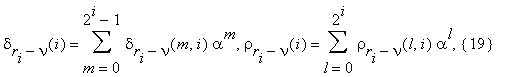
вычисляются числа
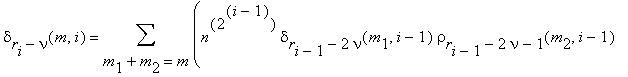
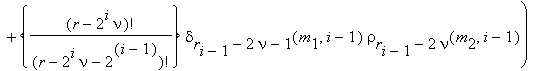
0 ≤ m1 ≤ 2i–1–1 , 0 ≤ m2 ≤ 2i–1 .
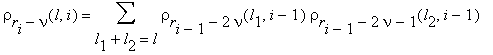
0 ≤ l1 ≤ 2i–1 , 0 ≤ l2 ≤ 2i–1 .
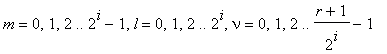
Заметим, что умножение на степень α и вычисление δ и ρ , так же как и деление δ на ρ , не производится до последнего шага.
Перед i+1 -ым шагом (1 ≤ i ≤k , 2i–1 < μ ≤ 2i) мы редуцируем многочлены (19) по модулю многочлена g(x) при x = α . Таким образом, если
где pt–1 , ..., p0 , qt , ..., q0 целые, t = 2i , то мы делим P(x) и Q(x) на g(x) с остатками:
где P1(x) и Q1(x) есть многочлены с рациональными коэффициентами, причем степени P1(x) и Q1(x) не превышают μ–1 . Отсюда и из (14) получаем
то есть в (18) имеем
Домножая, если нужно, числитель и знаменатель дроби (20) на целый общий множитель, получаем в числителе и знаменателе дробей «из скобок» многочлены с целыми коэффициентами степени не большей, чем μ–1 .
Начиная с шага i , на каждом шаге i , i+1 , ... , k , производится редукция многочленов от α , расположенных в числителе и знаменателе βξ(j) по модулю g(x) . Поскольку коэффициенты g(x) , так же как и степень g(x) являются абсолютными постоянными, то значения этих коэффициентов, участвующие в вышеописанных редукциях могут возрасти лишь не более чем в gμ раз, где
что не влияет на оценку сложности проводимых вычислений. На последнем, k-ом, шаге такого процесса получаем
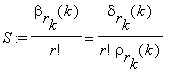
где
p, q ≤ μ–1 , и вычисляем δrk(k) , ρrk(k) и S, и следовательно Γ(α) с точностью 2–n+1. Сложность вычисления
Представленный метод БВЕ, метод быстрого суммирования специального вида рядов, позволяет вычислить любую элементарную трансцендентную функцию для любого аргумента, классические константы e, π, постоянную Эйлера γ, постоянные Апери и Каталана, такие высшие трансцендентные функции, как гамма-функцию Эйлера, гипергеометрические функции, сферические функции, цилиндрические функции и т. д. для алгебраических значений аргумента и параметров, дзета-функцию Римана для целых значений аргумента, дзета-функцию Гурвица для целого аргумента и алгебраических значений параметра, а также такие специальные интегралы, как интеграл вероятности, интегралы Френеля, интегральную экспоненциальную функцию, интегральные синус и косинус и т. д. при алгебраических значениях аргумента с оценкой сложности вычисления, близкой к оптимальной, а именно
В настоящее время только метод БВЕ даёт возможность быстро вычислять значения функций из класса высших трансцендентных функций, некоторые специальные интегралы математической физики и такие классические константы, как константы Эйлера, Каталана и Апери. Дополнительным преимуществом метода БВЕ является возможность распараллеливания основанных на БВЕ алгоритмов.
Понятие сложность вычисления возникло в результате развития вычислительных методов и теории информации.
Среди первых исследований в области теории информации были работы Гарри Найквиста [42] и Ральфа Хартли [19], где введено понятие меры информации.
Выше мы рассматривали битовую сложность, которая точнее всего определяет меру эффективности реальных вычислений. В то же время в разных задачах можно определять меру эффективности вычислений разными способами. Так, наряду с битовой, существуют алгебраическая, булева, колмогоровская, рациональная и т.д. сложности. Одни из них определяются количеством затрачиваемых на вычисление битовых, алгебраических и т.п. операций; другие — количеством шагов вычислительного процесса, например, количеством шагов работы машины Тьюринга.
Первым алгоритмом, проанализированным с точки зрения его сложности, был, по-видимому, алгоритм Евклида вычисления наибольшего общего делителя двух целых чисел. Мерой его сложности служило количество шагов-делений в этом алгоритме. Оценки сложности алгоритма Евклида получили [48] Aнтуан-Андрэ-Луи Рейно (грубая оценка числа шагов алгоритма, 1811 г.), Пьер-Жозеф-Этьен Финк (оценка шагов алгоритма, близкая к оптимальной, 1841 г.) и Габриель Ламе (оптимальная оценка, 1844 г.). Последний результат известен в литературе, как теорема Ламе.
Построение алгоритмов вычисления широкого класса функций с оценкой битовой
сложности, близкой к оптимальной, а также получение нетривиальных нижних оценок битовой
сложности
— основные задачи в той области вычислительной математики, которая
называется
быстрые алгоритмы или быстрые вычисления. В настоящее время здесь остаётся
много
нерешённых проблем, таких как
—
получение нетривиальной оценки снизу сложности умножения или сложности вычисления
трансцендентных функций;
—
построение быстрых алгоритмов вычисления высших трансцендентных функций
в трансцендентных точках;
—
построение быстрых алгоритмов вычисления таких констант, как
константа Бруна,
значения дзета-функции Римана в нецелых точках и т.д.
Эти и многие другие проблемы из области быстрых вычислений ещё ждут своего решения.
[1] В. Б. Алексеев, От метода Карацубы для быстрого умножения чисел к быстрым алгоритмам для дискретных функций. Труды Математического Института им. В. А. Стеклова, т. 218, с. 20-27 (1997).
[2] В. Б. Алексеев, С. А. Ложкин, Элементы теории графов, схем и автоматов. Изд. ВМиК МГУ, 58 с., Москва (2000).
[3] Г. И. Архипов, В. А. Садовничий, В. Н. Чубариков, Лекции по математическому анализу. Изд. Высшая школа, 695 с., Москва (1999).
[4] E. Bach, The complexity of number-theoretic constants. Info. Proc. Letters, N 62, pp. 145-152 (1997).
[5] D. H. Bailey, P. B. Borwein and S. Plouffe, On the rapid computation of various polylogarithmic constants. Math. Comp., v. 66, pp. 903-913 (1997).
[6] J. C. Bajard, J. M. Muller, Calcul et arithmétique des ordinateurs. Hermes Science, 226 pp. (2004).
[7] Л. А. Бассалыго, Замечание о быстром умножении многочленов над полями Галуа. Пробл. Пер. Инф., N 1, pp. 101-102 (1978).
[8] Ю. В. Бендерский, Быстрые вычисления. Доклады Академии Наук СССР, т. 223, N 5, с. 1041-1043 (1975).
[9] J. M. Borwein and P. B. Borwein, Pi and the AGM. Wiley, 414 pp., New York (1987).
[10] J. M. Borwein, D. M. Bradley and R. E. Crandall, Computational strategies for the Riemann zeta function. J. of Comput. Appl. Math., v. 121, N 1-2, pp. 247-296 (2000).
[11] R. P. Brent, Fast Multiple-Precision Evaluation of Elementary Functions. ACM, v. 23, N 2, pp. 242-251 (1976).
[12] R. P. Brent and E. M. McMillan, Some new algorithms for high-precision computation of Euler's constant. Math. Comp., vol. 34, pp. 305-312 (1980).
[13] B. C. Carlson, Algorithms involving arithmetic and geometric means. Amer. Math. Monthly, v. 78, pp. 496-505 (1971).
[14] B. C. Carlson, An algorithm for computing logarithms and arctangents. Math. Comp., v. 26, pp. 543-549 (1972).
[15] S. A. Cook, On the minimum computation time of functions. Thesis, Harvard University (1966).
[16] D. Coppersmith and S. Winograd, On the asymptotic complexity of matrix multiplication. SIAM Journal on Computing, v. 11, N 3, pp. 472-492 (1982).
[17] С. Б. Гашков, О сложности интегрирования рациональных дробей. Труды Математического Института им. В. А. Стеклова, т. 218, с. 122-133, (1997).
[18] С. Б. Гашков, В. Н. Чубариков, Арифметика. Алгоритмы. Сложность вычислений. Изд. Высшая школа, 2-е изд., 320 с., Москва (2000).
[19] R.V.L. Hartley, Transmission of Information. Bell System Technical Journal, v. 7, pp. 535-563 (1928).
[20] А. Карацуба и Ю. Офман, Умножение многозначных чисел на автоматах. Доклады Академии Наук СССР, т. 145, 2, с. 293-294 (1962).
[21] A. Karacuba, Berechnungen und die Kompliziertheit von Beziehungen. EIK, N 11, s. 10-12 (1975).
[22] А. А. Карацуба, Сложность вычислений. Труды Математического института им. Стеклова, т. 211, с. 169-183 (1995).
[23] Е. А. Карацуба, Быстрое вычисление exp(x). Проблемы передачи информации, т. 26, N 3, с. 109, Хроника, 17-ая Всесоюзная школа по теории информации и её приложениям (1990).
[24] Е. А. Карацуба, О новом методе быстрого вычисления трансцендентных функций. Успехи Математических Наук, т. 46, N 2 (278), с. 219-220 (1991).
[25] Е. А. Карацуба, О быстром вычислении трансцендентных функций. Доклады Академии Наук СССР, т. 319, N 2, с. 278-279 (1991).
[26] Е. А. Карацуба, Быстрое вычисление трансцендентных функций. Проблемы передачи информации, т. 27, N 4, с. 87-110 (1991).
[27] Е. А. Карацуба, Быстрое вычисление ζ(3). Проблемы передачи информации, т. 29, N 1, с. 68-73 (1993).
[28] Catherine A. Karatsuba, Fast evaluation of Bessel functions. Integral Transforms and Special Functions, v. 1, N 4, pp. 269-276 (1993).
[29] Е. А. Карацуба, Быстрое вычисление дзета-функции Римана ζ(s) для целых значений аргумента s. Проблемы передачи информации, т. 31, N 4, с. 69-80 (1995).
[30] Е. А. Карацуба, О быстром вычислении дзета-функции Римана для целых значений аргумента .Доклады Академии Наук СССР, т. 349, N 4, с. 463 (1996).
[31] Е. А. Карацуба, Быстрое вычисление дзета-функции Гурвица и L-рядов Дирихле. Проблемы передачи информации, т. 34, N 4, с. 342-353 (1998).
[32] Ekatharine A. Karatsuba, Fast evaluation of hypergeometric function by FEE. Computational Methods and Function Theory (CMFT'97), N. Papamichael, St. Ruscheweyh and E. B. Saff, eds., World Sc. Pub., pp. 303-314 (1999).
[33] E. A. Karatsuba, On the computation of the Euler constant γ. University of Helsinki preprint, 21 pp. (1999); J. of Numerical Algorithms, v. 24, pp. 83-97 (2000).
[34] E. A. Karatsuba, Fast computation of ζ(3) and of some special integrals, using the polylogarithms, the Ramanujan formula and it's generalization. J. of Numerical Mathematics BIT, v. 41, N 4, pp. 722-730 (2001).
[35] E. A. Karatsuba, Fast computation of some special integrals of mathematical physics. Scientific Computing, Validated Numerics, Interval Methods , W. Krämer, J. W. von Gudenberg, eds., pp. 29-41 (2001).
[36] Д. E. Kнут, Искусство программирования на ЭВМ. т. 2, Изд. Мир, 724 с., Москва (1977).
[37] А. Н. Колмогоров, О некоторых асимптотических характеристиках вполне ограниченных метрических пространств. Доклады Академии Наук СССР, т. 108, N 3, с. 385-388 (1956).
[38] А. Н. Колмогоров, Теория информации и теория алгоритмов. Изд. Наука, 303 с., Москва (1987).
[39] J. Landen, An investigation of a general theorem for finding the length of any arc of any conic hyperbola, by means of two elliptic arcs, with some other new and useful theorems deduced therefrom. Philos. Trans. Royal Soc. London v. 65, pp. 283-289 (1775).
[40] D. W. Lozier and F. W. J. Olver, Numerical Evaluation of Special Functions. Mathematics of Computation 1943-1993: A Half -Century of Computational Mathematics, W. Gautschi, eds., Proc. Sympos. Applied Mathematics, AMS, v. 48, pp. 79-125 (1994).
[41] В. И. Нечаев, Элементы криптографии. Основы теории защиты информации. Изд. Высшая школа, 110 с., Москва (1999).
[42] H. Nyquist, Certain factors affecting telegraph speed. Bell System Technical Journal, v. 3, pp. 324-346 (1924).
[43] V. Ya. Pan, Strassen's algorithm is not optimal. Proc. ACM Symp. on the Found. of Comp. Science, pp. 166-176 (1978).
[44] E. Salamin, Computation of π using arithmetic-geometric mean. Math. Comp., vol. 30, N 135, pp. 565-570 (1976).
[45] A. Schönhage, Schnelle Multiplikation grosser Zahlen. Computing, v. 1, pp. 182-196 (1966).
[46] A. Schönhage und V. Strassen, Schnelle Multiplikation grosser Zahlen. Computing, v. 7, pp. 281-292 (1971).
[47] A. Schönhage, A. F. W. Grotefeld and E. Vetter, Fast Algorithms — A Multitape Turing Machine Implementation. BI-Wiss.-Verl., 300 pp., Zürich (1994).
[48] J. Shallit, Origins of the Analysis of the Euclidean Algorithm. Historia Mathematica, v. 21, pp. 401-419 (1994).
[49] C. L. Siegel, Transcendental numbers. Princeton University Press, 102 pp., Princeton (1949).
[50] V. Strassen, Gaussian elimination is not optimal. J. Numer. Math., N 13, pp. 354-356 (1969).
[51] А. Л. Тоом, О сложности схемы из функциональных элементов, реализующей умножение целых чисел. Доклады Академии Наук СССР, т. 150, N 2, с. 496-498 (1963).
О методе БВЕ в статье:
Е. А. Карацуба,
«Быстрое вычисление дзета-функции
Римана ζ(s) для целых значений аргумента s».
Проблемы передачи информации, т. 31, № 4, с. 69-80 (1995).