group homepage                                                                                                          Russian version

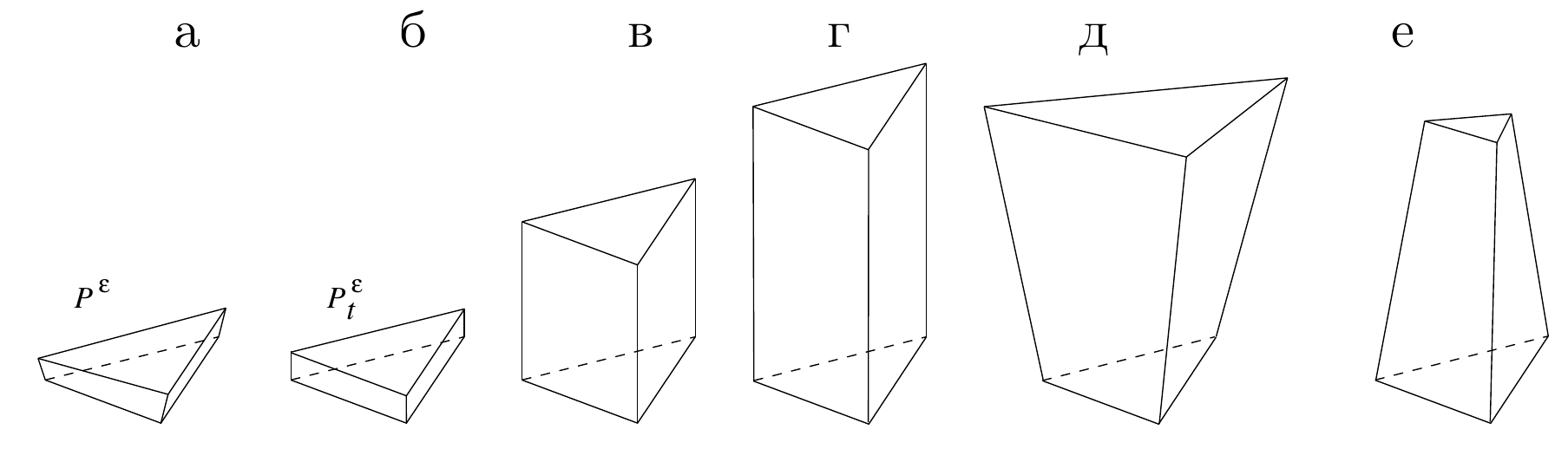
prismatic_qi3d_poly project: generator of thick prismatic layers around complex bodies.

New prismatic mesh generator based on elastic springback is developed. Thin layer of highly compressed elastic cells is glued to the boundary of domain. After that outer boundary of prisms is freed and after relaxed springback new equilibrium elastic layer is established with  prescribed   prism height distribution.



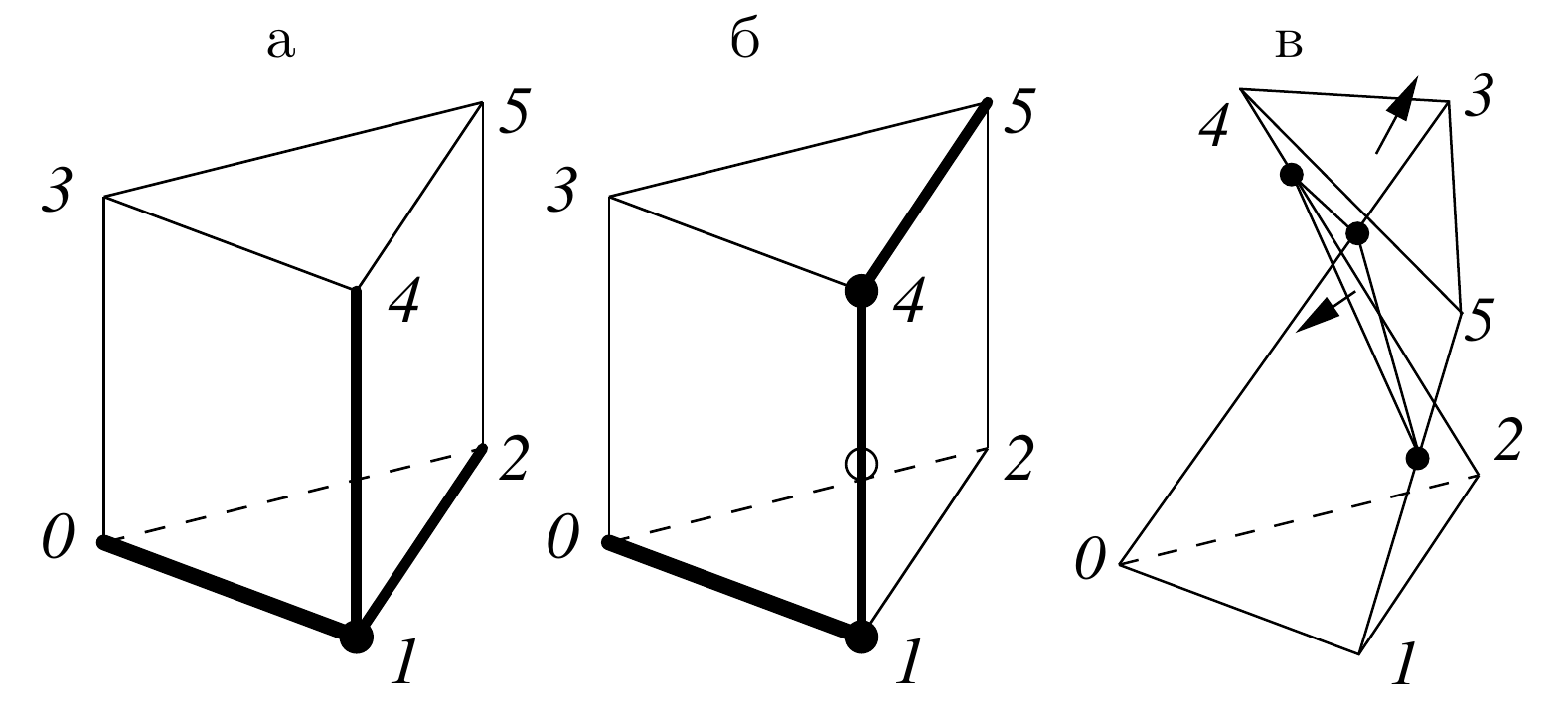
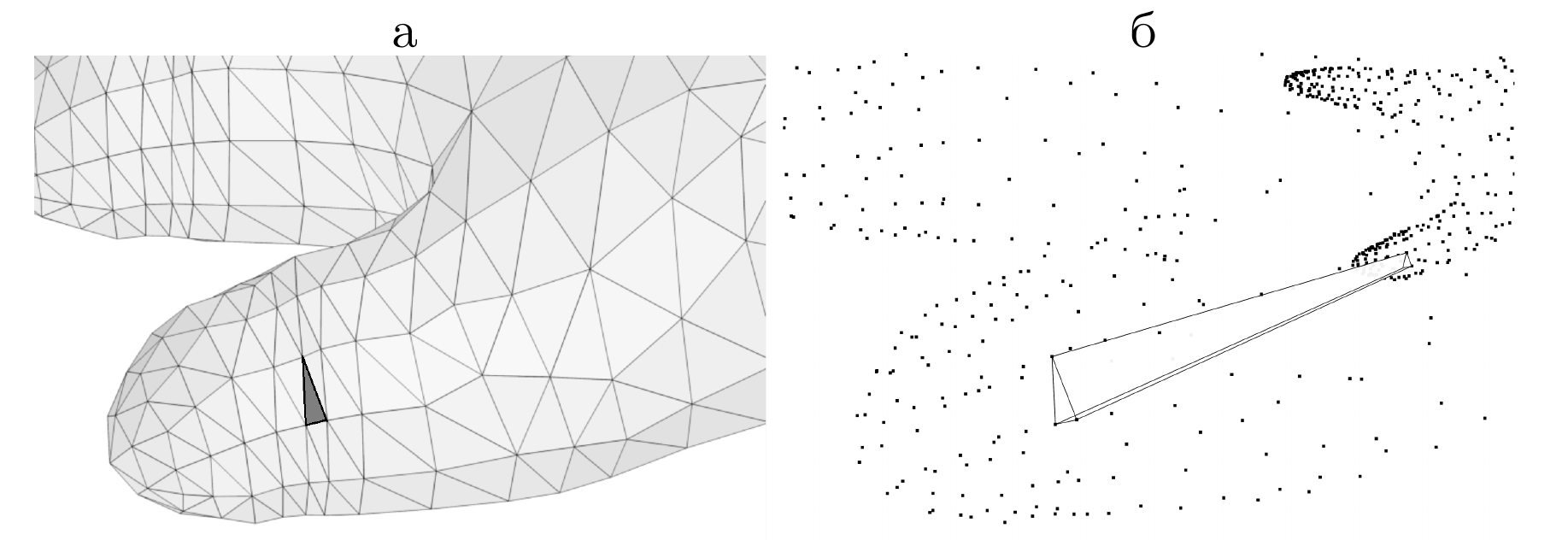
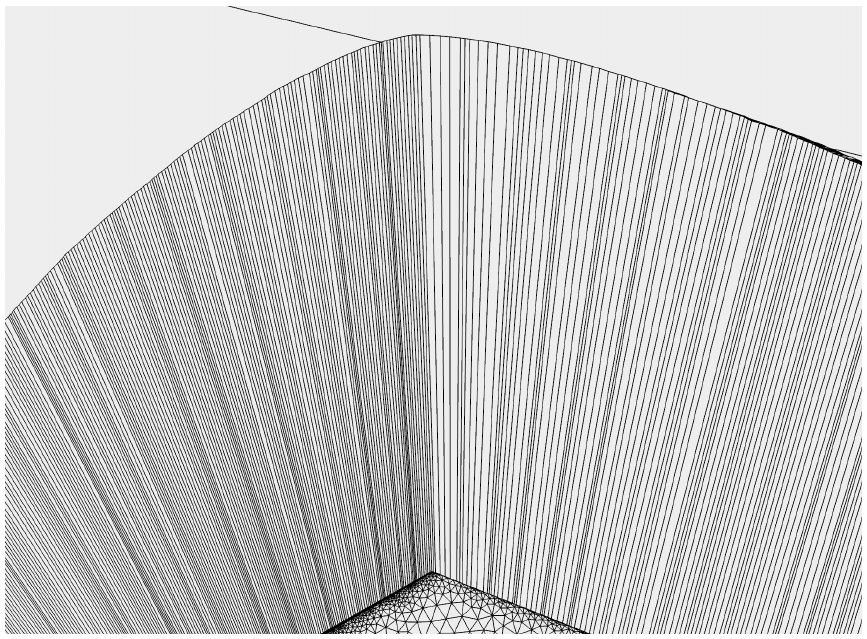
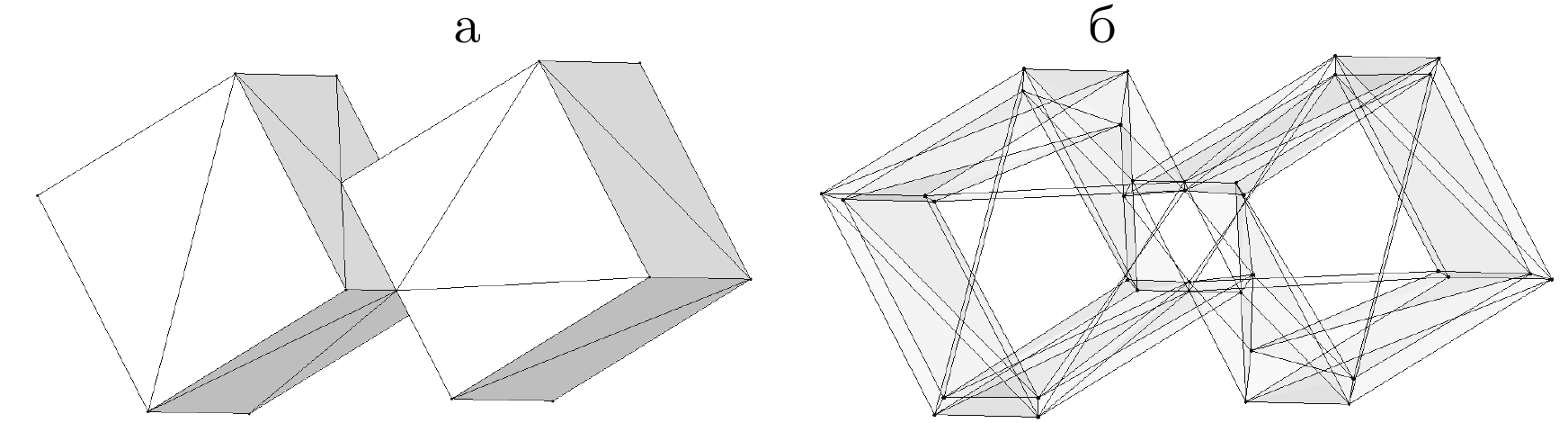
In order to approximate hyperelastic functionals with polyconvex elastic potentials finite element method is applied with a special set og geometric quadratures. Depending on the choice of the quadratures, the finiteness of the discrete energy may or may not impose nondegeneracy of elastic cells. The most typical degeneracy is due to cell twisting shown in figure which may arise when simple vertex-based quadratures are used.




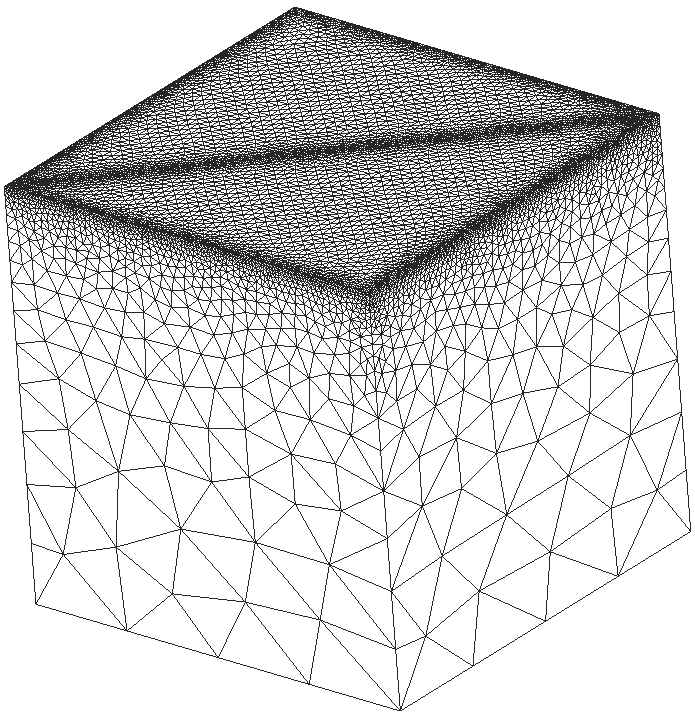
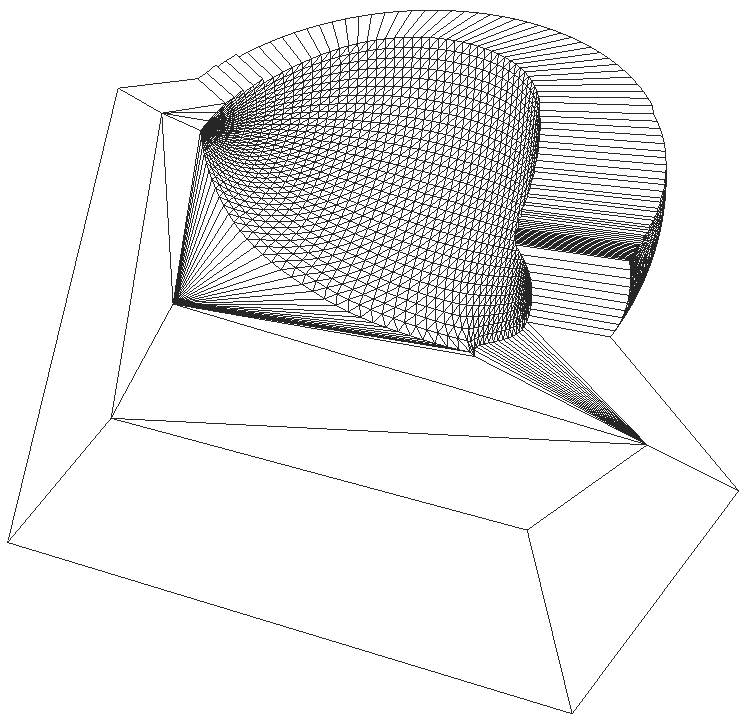
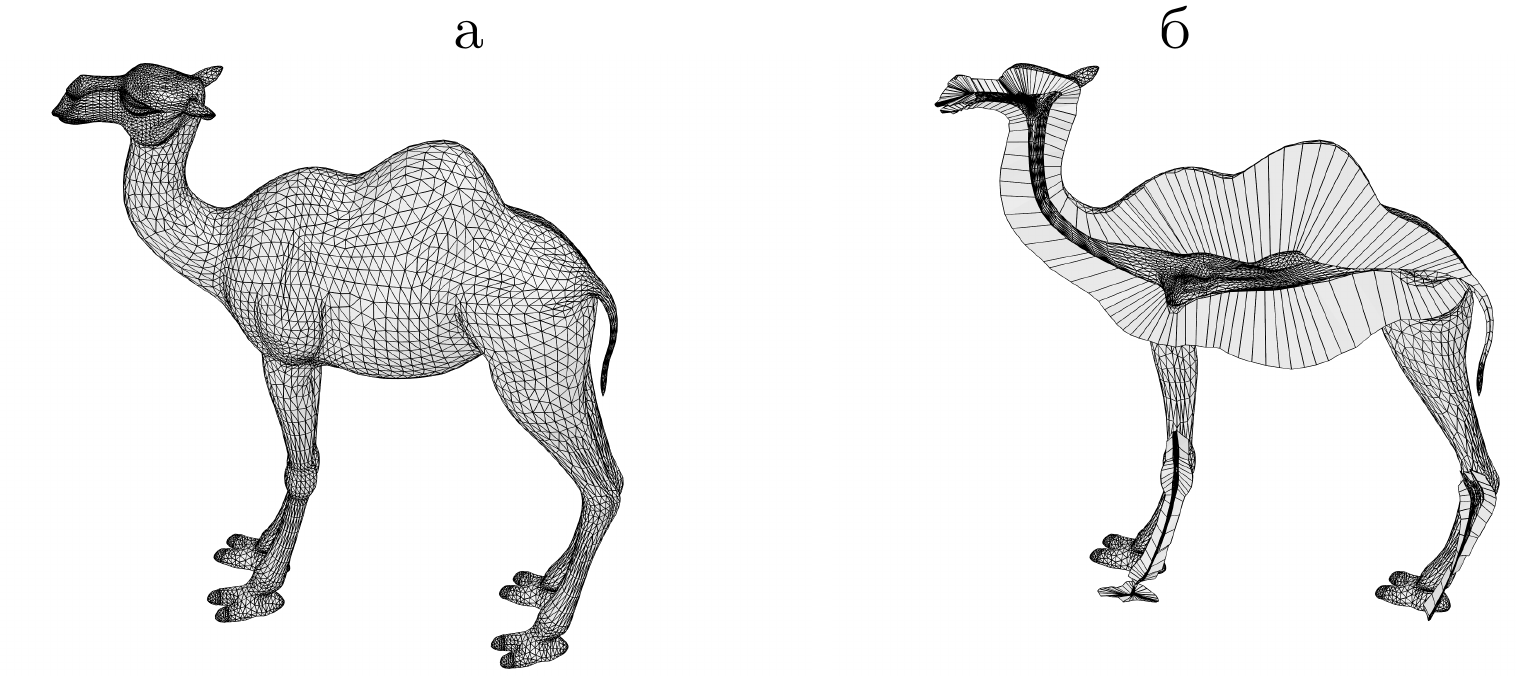
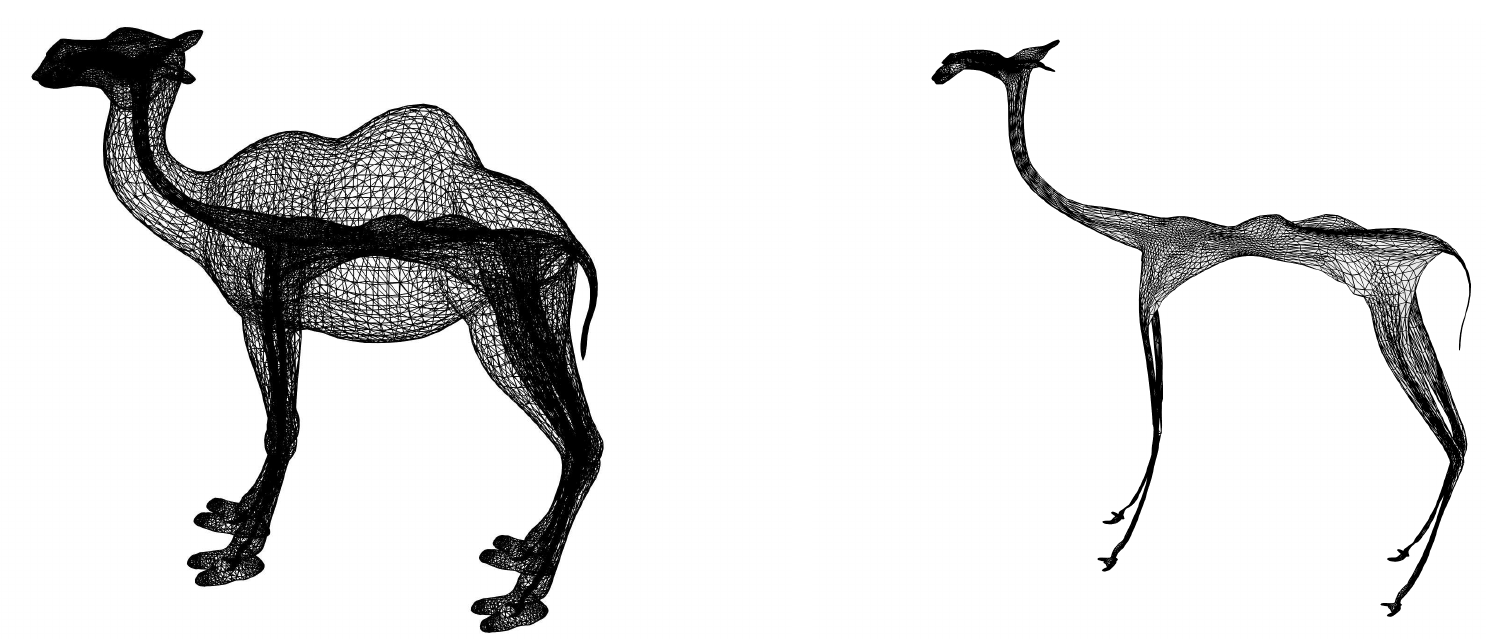
Camel model and one-cell-wide prismatic layer are shown below.



When 6-vertex quadrature rule is used for a triangular bilinear prism the twisted prisms appear:


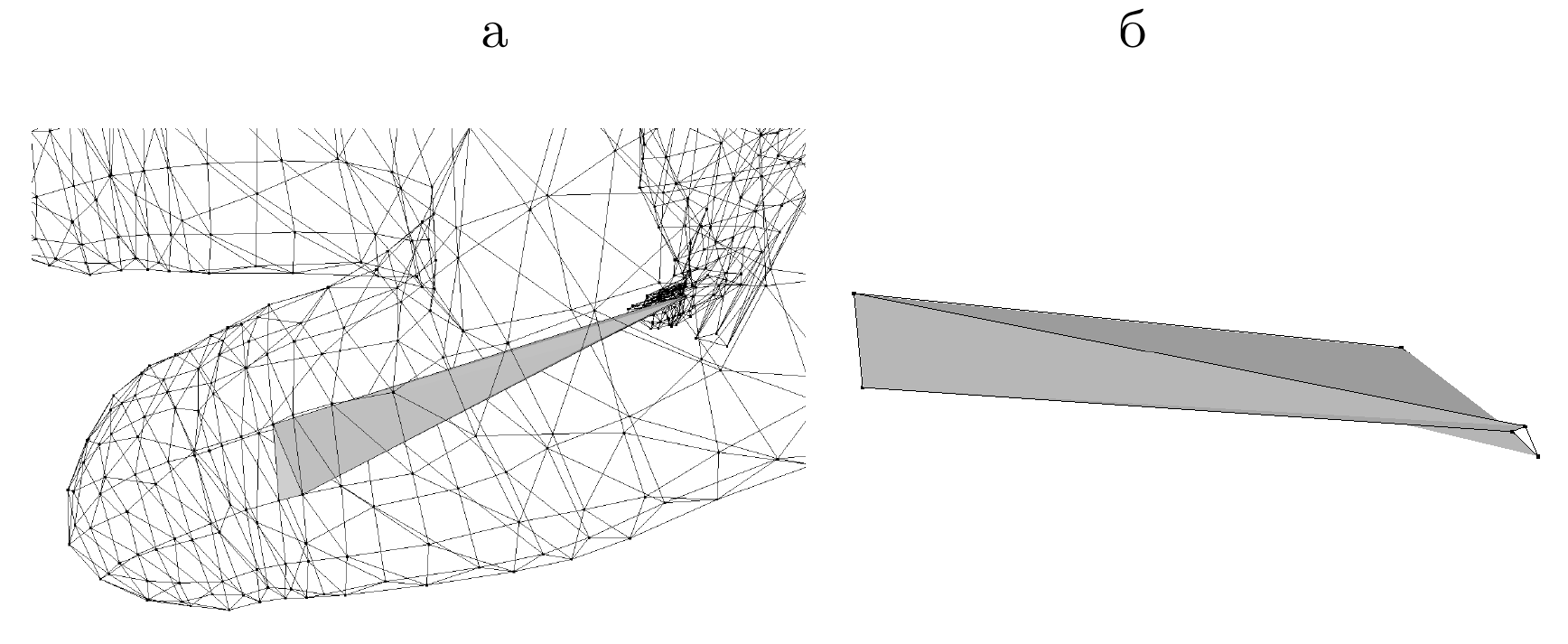
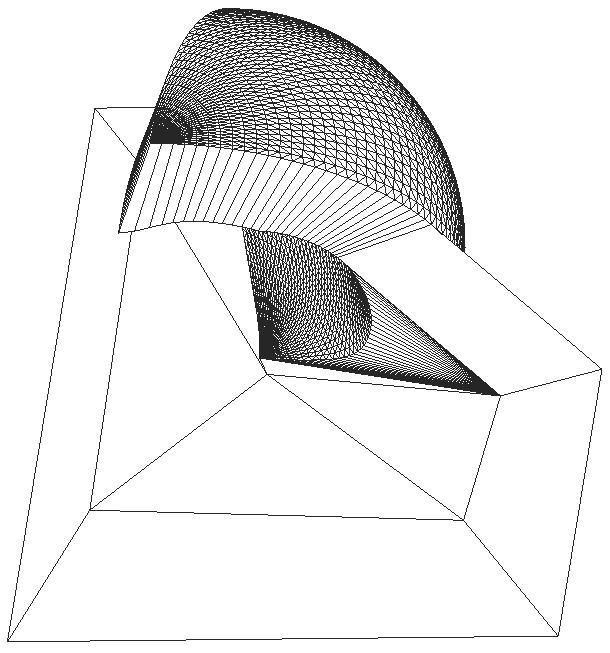
Special geometric 12-node quadrature guarantees that all prisms are nondegenerate. The same prism is shown.



In fact generator of this prismatic layers provides the tool for construction of generalized skeleton of 3d domain.



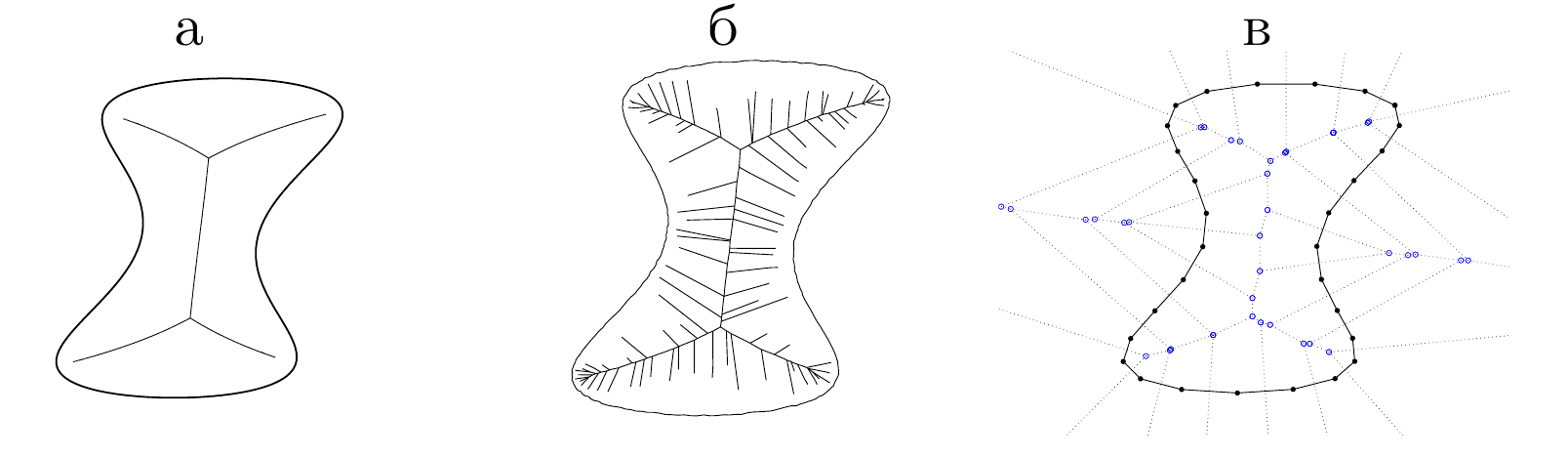
Such generalized skeleton is quite different from conventional medial axis. Note that medial axis is the set of centers of  the interior balls which touch the boundary of domain at least in two points. The concept of medial axis is quite useful for prismatic layer generation since it encodes the information about mutual positions of the domain boundary fragments. However direct application of medial axis does not allow construction of thick layers.



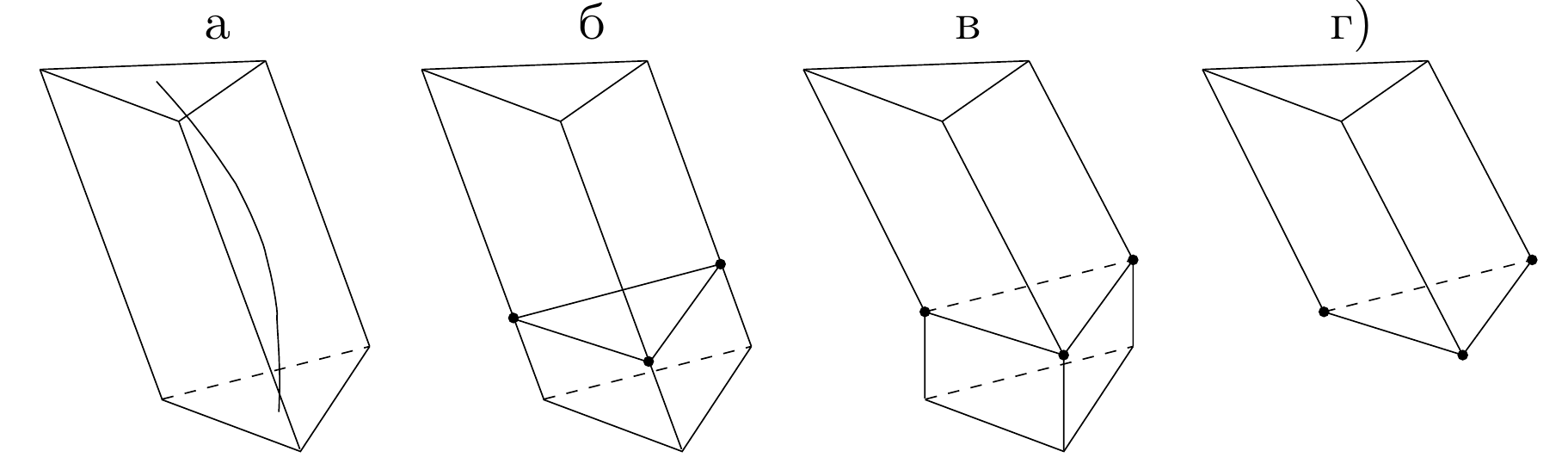
As soon as one-cell-wide prismatic layer with prescribed thickness is constructed, advancing variational orthogonalization procedure is applied. In this algorithm nonorthogonality measure if very close to zero in internal one third of layer.



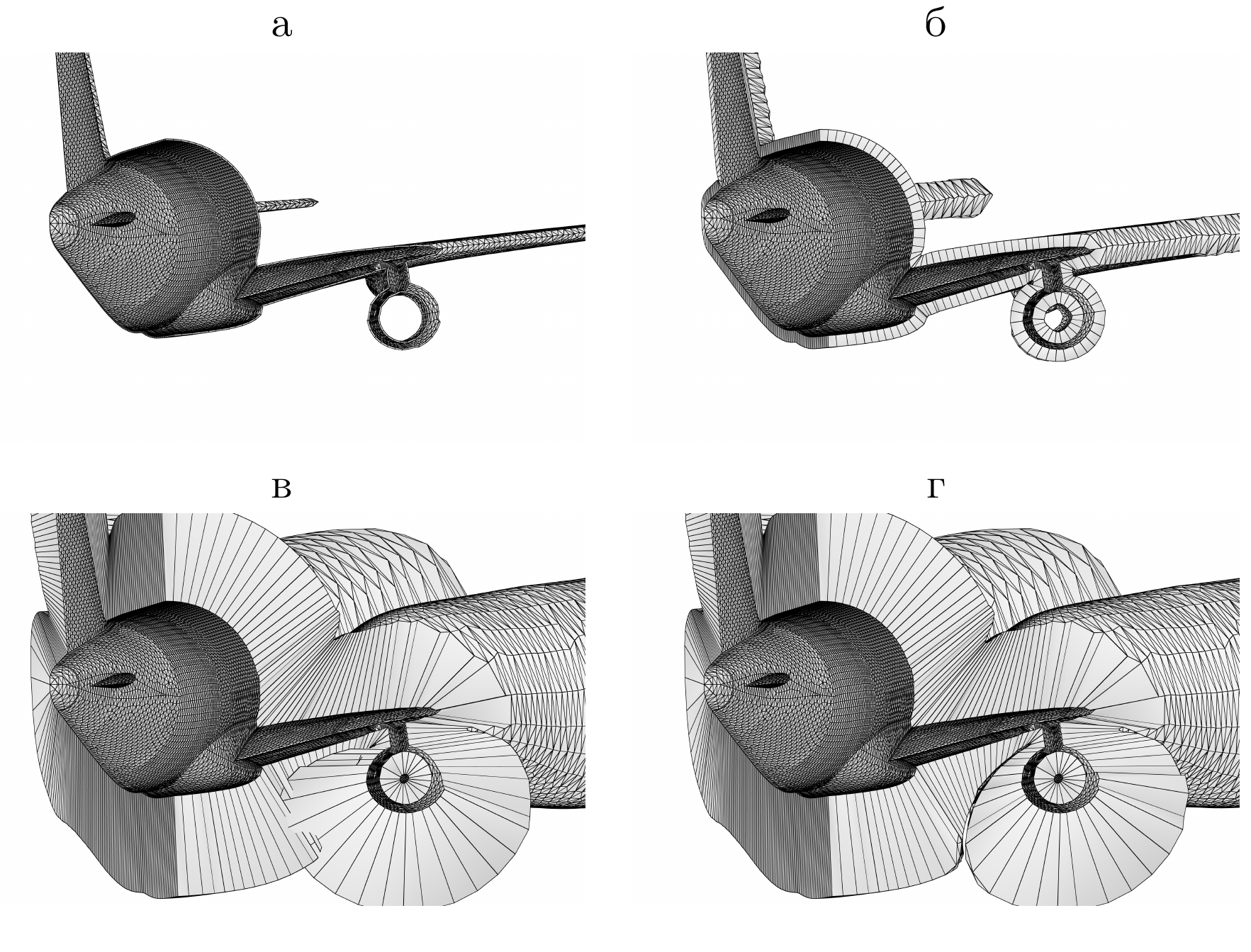
Prismatic mesh generation around aircraft: a) initial thin layer; b) prism growth due to elastic springback; c) maximal single-cell layer; d) excessive material cut-off to eliminate self-intersections.




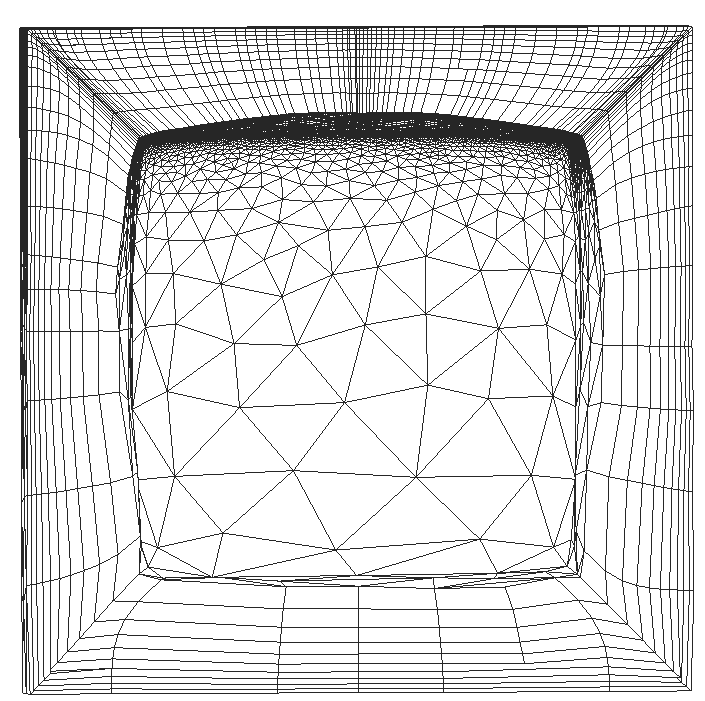
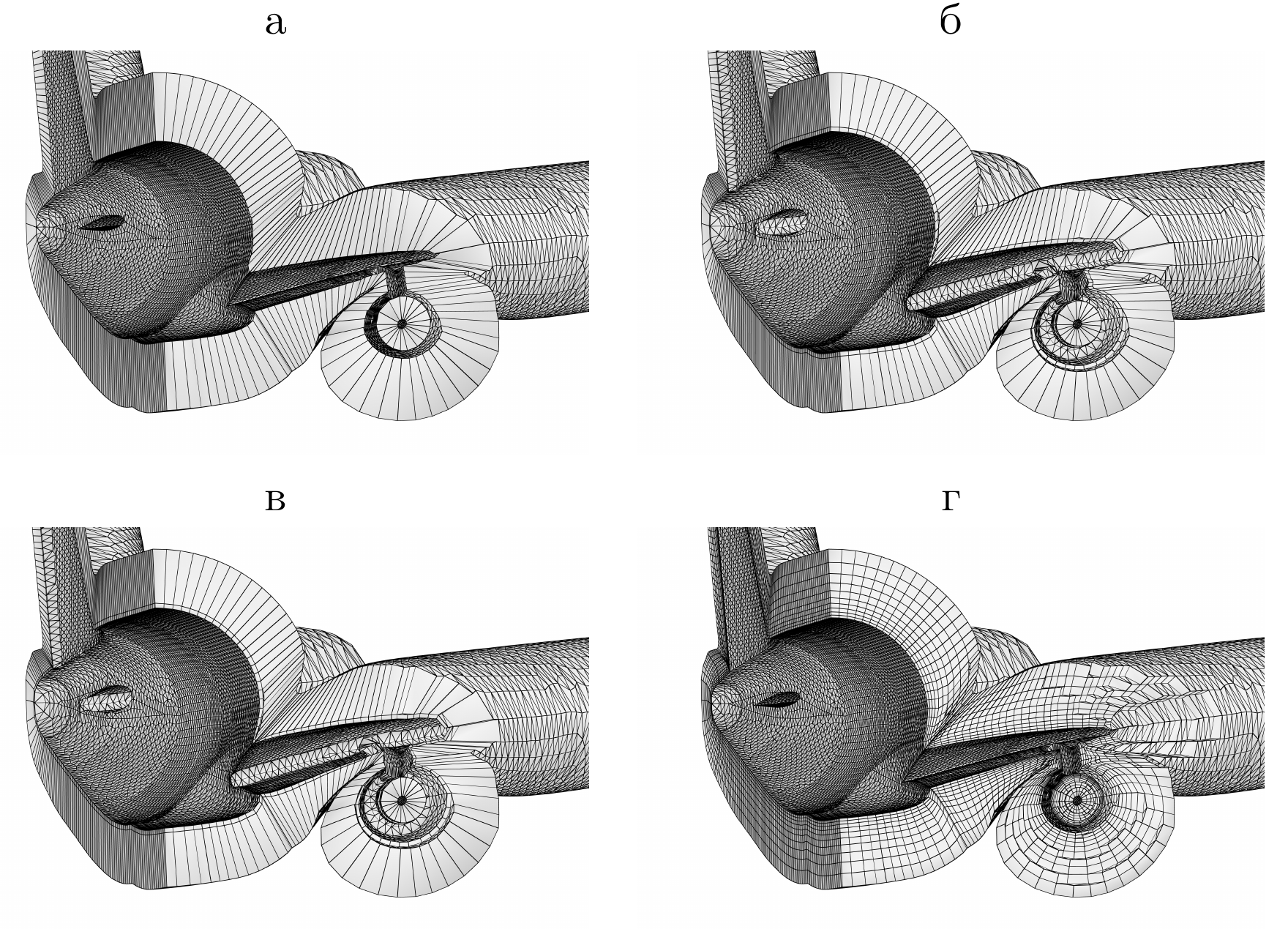
Continuation: a) outer boundary of layer is smoothed; b) first step of orthogonalization; c) intermediate step of orthogonalization;
d) final mesh which is orthogonal near boundary.



Variational method allows to construct prismatic layers which are almost insensitive to the size and quality of the surface cells. Sensibility of layer thickness to the ravines and dents on the surface is relatively weak which makes big difference in comparison to methods based on the medial axis concept.

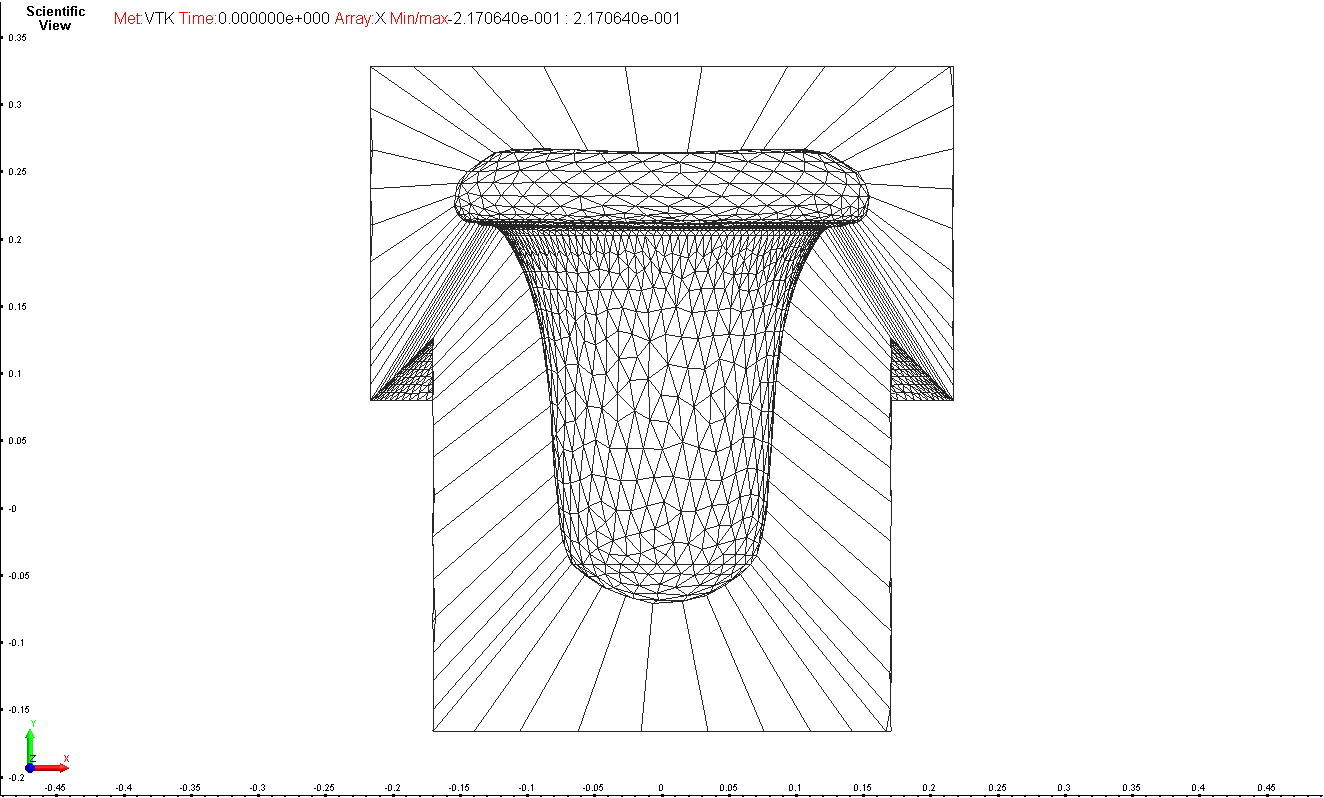
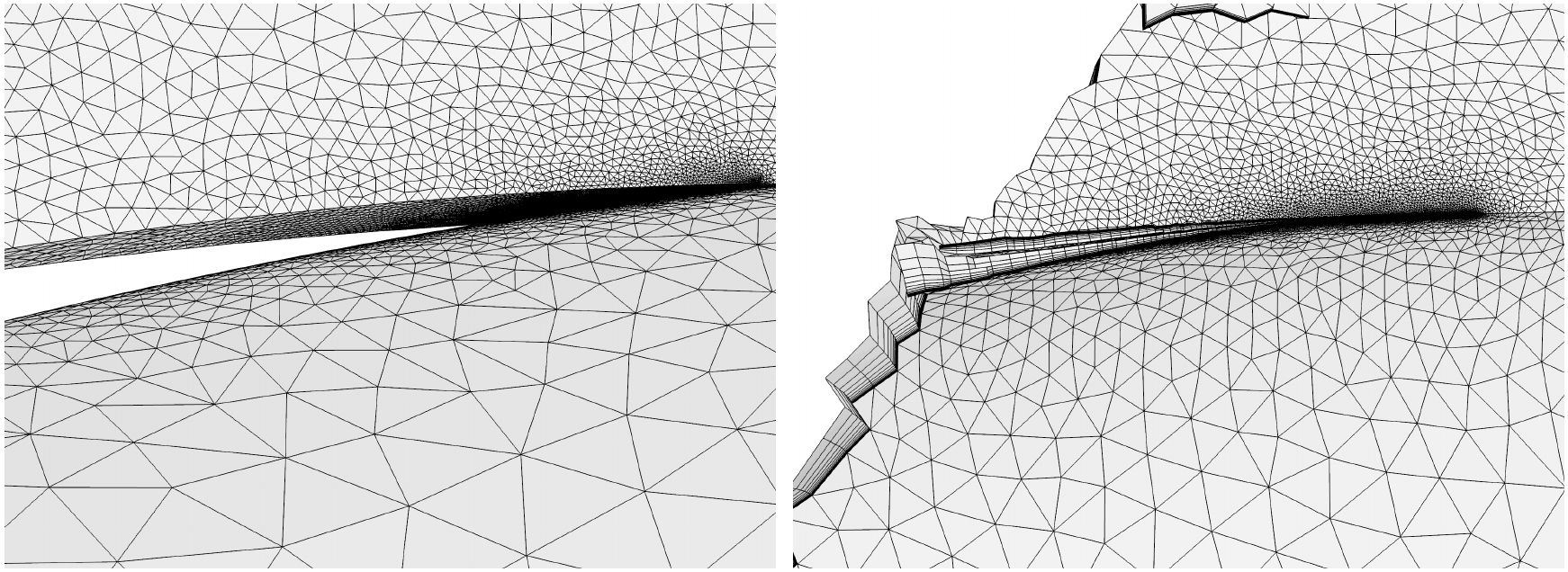
Example of surface mesh with high variation of the mesh size. It is clear that computed offset and prismatic layer is almost insensitive to the cell size.
However, presence of very small cells leads to higher height to base ratio for offset prisms which makes the springback problem more stiff and requires larger number of iterations.



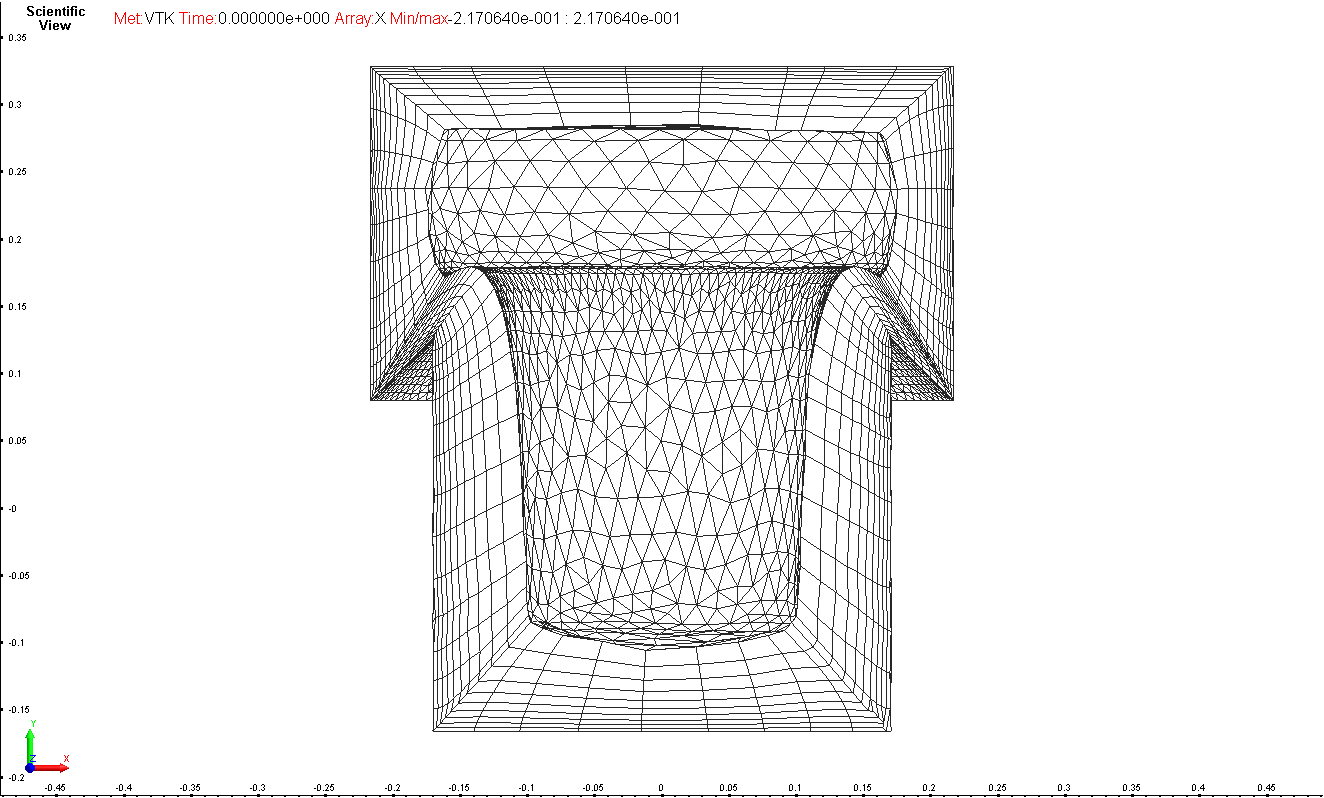
Sample layer in the presence very large and very small surface cells. Arbitrary bad surface cell shapes are present (dimensionless distortion measure reaches  10⁴-10⁵).


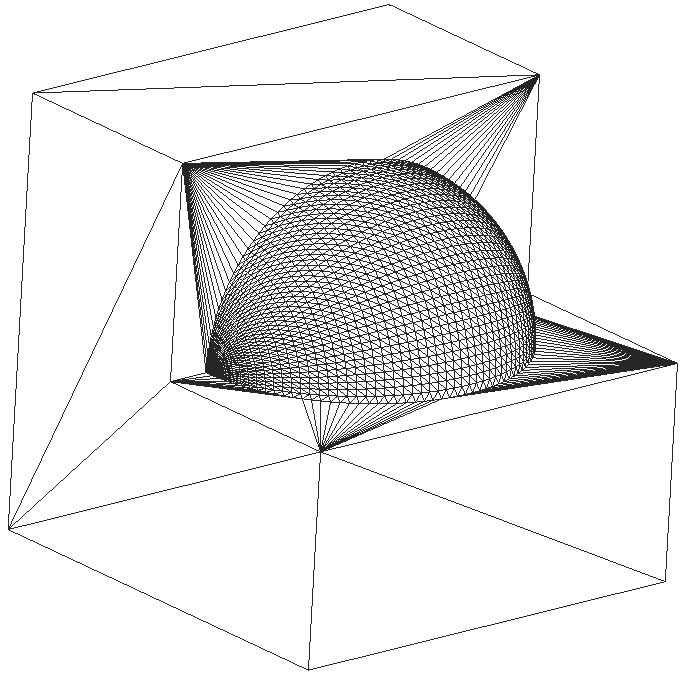
Sample prismatic layer in the presence of the sharp outcoming corners.


Sample prismatic layer in the presence of sharp outcoming and incoming corners placed close to each other..


Variational method allows to solve very stiff elastic springback problems. When offset value is large and cell size on the surface is small the height to base ratio for offset prisms can be above 1000.



Example of badly posed layer generation problem with very narrow slits and extremely small incoming and outcoming angles.



Example of prismatic mesh layer for hard test case.




Construction of prismatic mesh layer around test model of TsAGI re-entry vehicle.



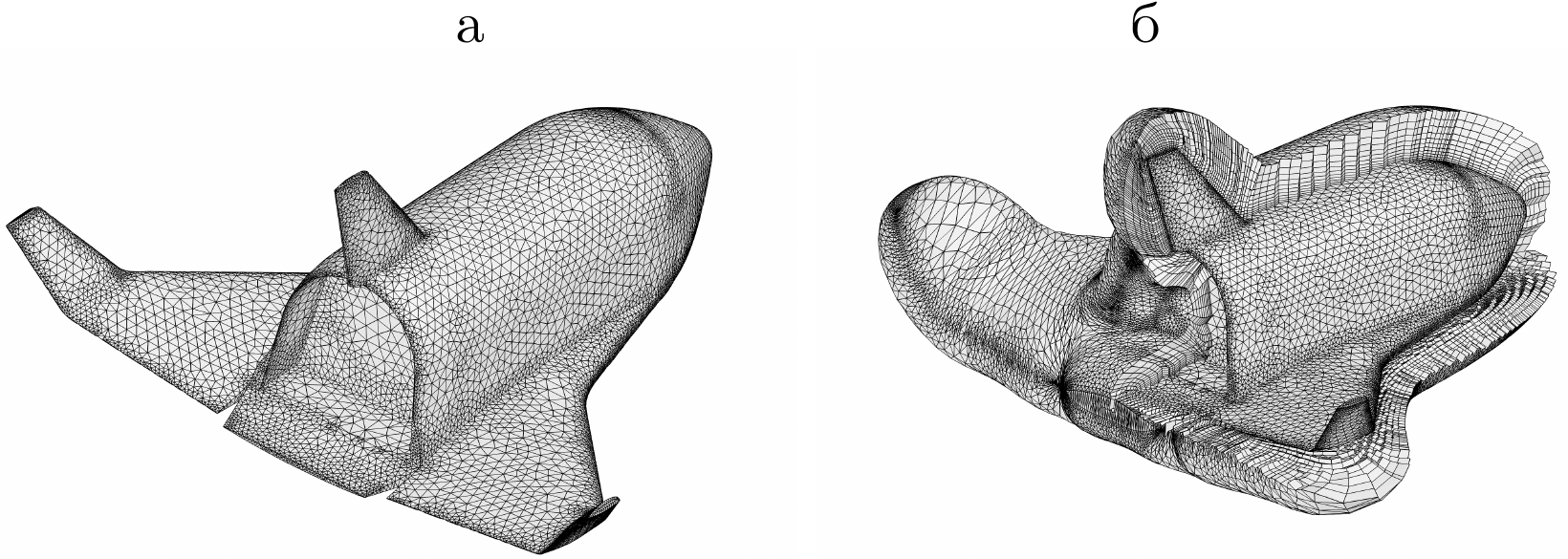
Sharp incoming and outcoming corners near rudder fins and prismatic mesh which is orthogonal near boundary.



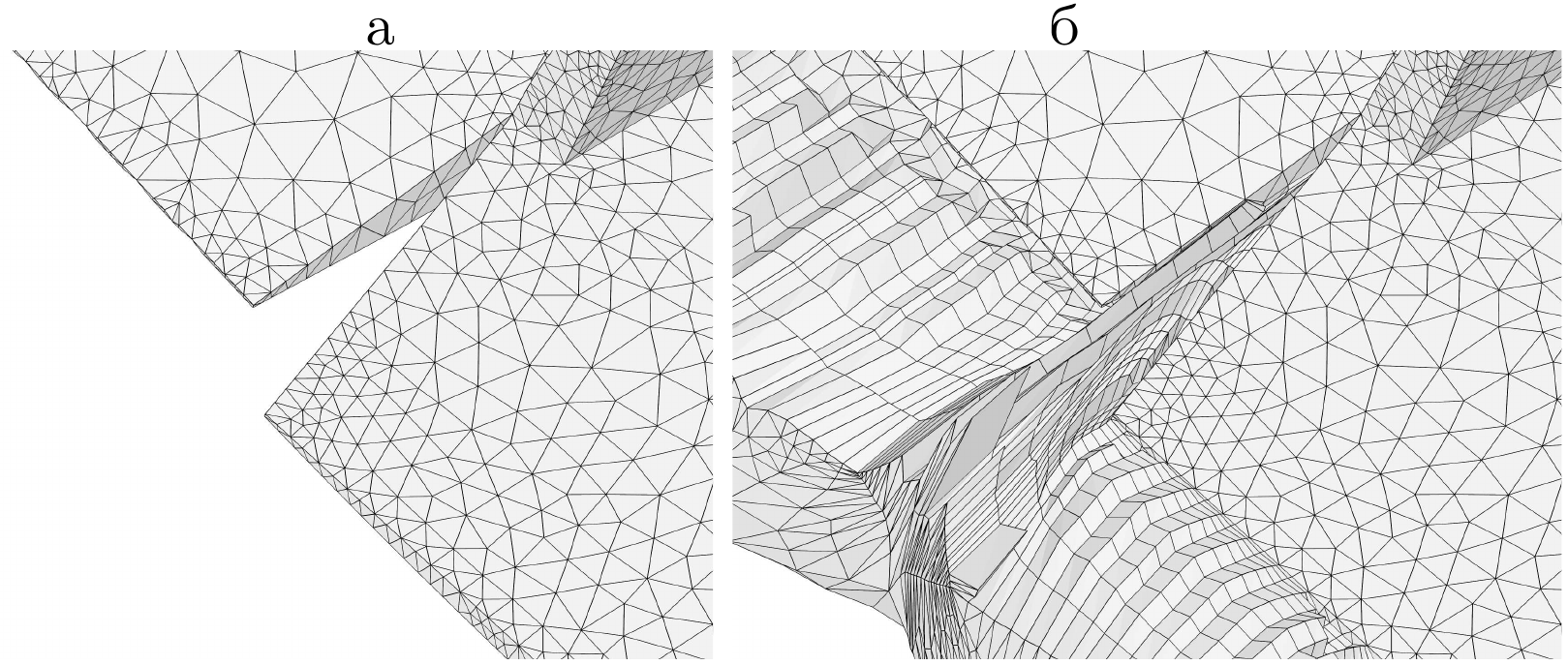
Prismatic mesh generators allows to mesh the domain as a whole.



In some cases surface of the model is not Lipshitz-continuous at certain conical vertices. This special case is included into general layer mesh generation scheme.