|
When an algorithm |
|
|
The concept of the complexity of an algorithm is measured as the time or storage space cost required to execute it in the worst or average case. This concept provides a mathematical definition for the rather vague term "hardness," which is sometimes used to characterize algorithms. |
|
When an algorithm |
|
|
|
For a fixed input size, the inputs of an algorithm can vary, in which case the cost generally varies as well.
The worst-case time and space complexities of an algorithm
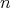 regarded as an argument of
regarded as an argument of 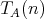 and and
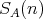 is the range of the size
is the range of the size  . .
|
|
|
|
|
The worst-case complexity determines a tight upper bound for the possible cost of the algorithm on inputs of given size. It cannot be ruled out that in some cases this bound is rather large, while inputs corresponding to the worst case are rarely encountered among all inputs of given size. |
|
|
Question:
Suppose that an algorithm
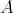 consists of the sequential
(one after another) execution of algorithms consists of the sequential
(one after another) execution of algorithms 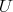 and
and 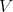 , having respective complexities , having respective complexities
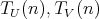 . Is it true that . Is it true that
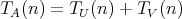 ? ?
|
|
Question:
Let
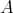 and and 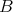 be algorithms. Is it true that
be algorithms. Is it true that 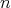 for all
for all 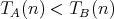 implies implies
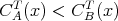 for all possible inputs
for all possible inputs 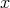 ? ?
|
|
Question:
Is it true that the space complexity of selection sort (with the array length
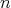 being the input size) is bounded above by a quantity independent of
being the input size) is bounded above by a quantity independent of
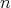 ? ?
|
|
Question:
Let an algorithm
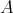 be associated with two, say, time complexities
be associated with two, say, time complexities 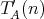 and
and 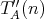 . For example, . For example,
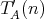 and and 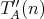 can be complexities in terms of different operations. Define the complexity
can be complexities in terms of different operations. Define the complexity
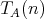 , considering operations of both types. Is it
true that , considering operations of both types. Is it
true that 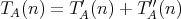 ? ?
|
|
When discussing average-case complexity, we consider only the situation when, for each fixed input size
|
|
|
|
Given an arbitrary algorithm |
|
|
|
|
If an algorithm is repeatedly applied to inputs of given size, it can be expected that the arithmetic mean of the costs is close to the average-case complexity of this algorithm. However, it is assumed in this case that the inputs of given size are appropriately assigned some probabilities, while this assumption has to be justified (the typical assumption that all the inputs of each size are equiprobable may appear groundless in a particular situation). |
|
|
|
|
|
Question:
Is it true that the average-case complexity of an algorithm requires that
a probability distribution be specified:
|
|
Question:
Let an algorithm
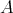 be assigned two average-case time complexities
be assigned two average-case time complexities
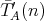 and
and 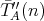 . For example, . For example,
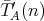 and and
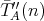 can be complexities measured as different operations. Let the complexity
can be complexities measured as different operations. Let the complexity
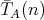 ,
be defined by considering operations of both types. Is it true that ,
be defined by considering operations of both types. Is it true that
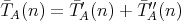 ? ?
|
|
Question:
Consider the set of all permutations of
 ,
assigning the probability ,
assigning the probability 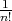 to each of them. For the permutation to each of them. For the permutation
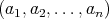 the number of its fixed points is defined as the number of indices
the number of its fixed points is defined as the number of indices
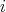 such that such that
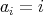 . (In sorting, fixed points do not need to
be swapped transfered, which can be used in some forms of sorting.) Is it true that,
for a fixed . (In sorting, fixed points do not need to
be swapped transfered, which can be used in some forms of sorting.) Is it true that,
for a fixed 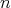 the expectation of the number of fixed points of the permutation is equal to:
the expectation of the number of fixed points of the permutation is equal to:
|
|
As was discussed above, the worst- and average-case complexities of an algorithm are both a function of a numerical argument-the input size. The growth of the complexity of a particular algorithm with increasing input size is frequently analyzed using asymptotic bounds of the form
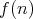 is on the order of is on the order of
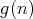 ”, or
“ ”, or
“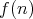 and and
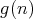 are of the same order”. are of the same order”.
|
|
|
|
A comparison of the complexities of different algorithms based on their asymptotic
complexity bounds can be made not for all types of such bounds.
For example, if algorithms |
|
|
|
|
|
|
|
Question:
Suppose that the polynomial
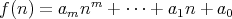 has a nonzero leading coefficient
has a nonzero leading coefficient 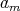 .
Which of the following assertions is true: .
Which of the following assertions is true:
|
|
Question:
Which of the following assertions is not true for the complexity
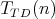 of the trial division algorithm (see Section 1), which is intended for testing the primality of
an integer
of the trial division algorithm (see Section 1), which is intended for testing the primality of
an integer  (we mean the complexity measured as the number of divisions): (we mean the complexity measured as the number of divisions):
|
|
Question:
Let the cost of any compass-and-straightedge construction in plane geometry be the number of lines
(circles or straight lines) drawn in the course of the construction. Consider the problem of constructing
a line segment whose length is
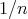 of that of the original segment, assuming that
of that of the original segment, assuming that 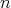 is the input size. Is there an algorithm for solving the problem whose complexity bound is
is the input size. Is there an algorithm for solving the problem whose complexity bound is
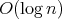 ? ?
|
|
We can consider different complexities according to the costs taken into account. Suppose that a time cost function gives the number of operations of some type, assuming that they require an identical runtime independent of the operand size and set equal to 1. Then we obtain an algebraic complexity measured as the number of operations of the given type. |
|
|
|
Bit time complexity is obtained when the number of bit operations is used as a cost function. In a similar fashion, the space algebraic and bit space complexities can be defined using the number of operations values of the considered type. |
|
|
|
|
Question:
It is well known that the multiplicative complexity of Gaussian elimination as applied to a system of
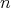 linear equations with linear equations with
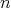 unknowns satisfies the bounds estimates unknowns satisfies the bounds estimates
|
|
Question:
Suppose that two positive integers
 and and
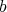 are multiplied using the additions are multiplied using the additions
 and
and 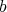 (denoted by
(denoted by 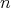 ).
Which of the following bounds is true for the complexity of this "supernaive" multiplication: ).
Which of the following bounds is true for the complexity of this "supernaive" multiplication:
|
|
Question:
Given a number initially equal to zero, a 1 is added to it at every step until
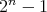 , ,
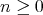 , is reached. All the additions are performed in columns
in the binary system. Is it true that , is reached. All the additions are performed in columns
in the binary system. Is it true that 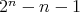 transfers of 1 to the next position on the left are required in these additions?
transfers of 1 to the next position on the left are required in these additions?
|
|
The concept of complexity is also considered in the case of randomized algorithms, i.e., algorithms making calls to a random number generator with a known distribution. |
|
|
|
Generally, the cost of a randomized algorithm is not uniquely determined by its input, but also depends on the generated random numbers. However, the averaged cost for each particular input gives a scalar numeric function on the set of inputs. As a result, the complexity of an algorithm can be treated following the general definition of complexity. |
|
|
|
|
As was previously discussed, the average-case complexity of a "usual" (deterministic) algorithm is of interest only if correct assumptions are made about the probability of occurrence of one or another input. The considered complexity of randomized algorithms is worst-case complexity but it is determined by the averaged costs. Nevertheless, this averaging can be trusted, since randomized algorithms make use of random number generators in which the probability distribution is fixed and independent of the inputs. |
|
|
|
|
|
Question:
Is it true that the determination of the averaged cost of a randomized algorithm requires specifying a probability distribution:
|
|
Question:
An array
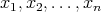 is said to contain a majority if more than half of its elements have identical values.
Let the operation of verifying whether two elements are equal be defined over the array
elements. This operation is called comparison. Given a majority-containing array, the goal
is to find an
is said to contain a majority if more than half of its elements have identical values.
Let the operation of verifying whether two elements are equal be defined over the array
elements. This operation is called comparison. Given a majority-containing array, the goal
is to find an 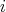 , ,
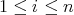 , such that the value , such that the value
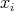 belongs to the majority of values of
belongs to the majority of values of 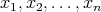 .
A possible randomized algorithm for solving this problem is that .
A possible randomized algorithm for solving this problem is that
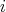 is chosen at random (a uniform probability distribution) and
it is then verified whether
is chosen at random (a uniform probability distribution) and
it is then verified whether
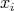 satisfies the above condition. The number of comparisons required for this verification is
satisfies the above condition. The number of comparisons required for this verification is
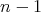 . If . If
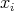 does not satisfy the condition, all
steps are repeated. Is it true that the complexity measured as the number of comparisons
in this randomized algorithm with does not satisfy the condition, all
steps are repeated. Is it true that the complexity measured as the number of comparisons
in this randomized algorithm with 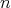 taken as an input size is less than
taken as an input size is less than 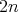 ? ?
|
|
Question:
Assume that there is a random number generator returning 0 with probability
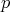 or 1 with probability
or 1 with probability  ; moreover, it is
only know about ; moreover, it is
only know about 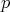 that that
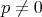 and
and 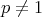 . This generator can be used to
design another one returning 0 or 1 with identical
probability . This generator can be used to
design another one returning 0 or 1 with identical
probability 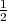 :
generating two digits in succession with the help of the original generator, we obtain
the combinations 0, 1 and 1, 0 with an identical nonzero probability (the combinations
0, 0 and 1, 1 are ignored). Consider the expected number :
generating two digits in succession with the help of the original generator, we obtain
the combinations 0, 1 and 1, 0 with an identical nonzero probability (the combinations
0, 0 and 1, 1 are ignored). Consider the expected number
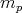 of calls to the original random number generator
that are required in the construction of a sequence of pairs until 0, 1 or 1, 0 occur.
Which of the following assertions is true: of calls to the original random number generator
that are required in the construction of a sequence of pairs until 0, 1 or 1, 0 occur.
Which of the following assertions is true:
|
|
|
In computational complexity theory, initial assumptions are made about a hypothetical computing device (known as a model of computation). |
|
A random-access machine (RAM) is used as such a model in some cases, while a Turing machine is chosen in other cases. |
|
|
|
|
The former model is closer to actual devices, while the latter is more formalized, which is frequently useful in the existence analysis of an algorithm with certain complexity properties. |
|
|
We will use the RAM model. The assumption that the size of a cell is unlimited leads to algebraic complexity, while the assumption that one bit is stored in a cell leads to time or space bit complexity. |
|
The considered concept of complexity is sometimes referred to as computational complexity (its possible special cases are algebraic and bit complexities) in order to distinguish it from descriptive complexity, which is somehow defined relying on the code of an algorithm. |
|
|
|
|
Only computational complexity is discussed below, and we continue to refer to it as complexity. |
|
Considering a class of algorithms for solving a problem yields a family of functions that are complexities (for example, time complexities) of algorithms in this class. Accordingly, we can discuss a lower bound for this family and the existence of a minimal function in it. |
|
|
|
If there is a minimal function in this family, then the corresponding algorithm is optimal in the considered class of algorithms. |
|
|
|
|
Question:
Is
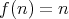 an asymptotic lower bound for the complexity of algorithms for
compass-and-straightedge division of a segment into
an asymptotic lower bound for the complexity of algorithms for
compass-and-straightedge division of a segment into
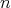 equal parts
with equal parts
with 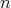 regarded as an input size (the cost of any compass-and-straightedge
construction in the plane is assumed to be the number of lines
(circles or straight lines) drawn in the course of the construction)?
regarded as an input size (the cost of any compass-and-straightedge
construction in the plane is assumed to be the number of lines
(circles or straight lines) drawn in the course of the construction)?
|
|
Question:
Consider the problem of computing
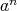 in a set with associative multiplication (i.e., in a semigroup), where
in a set with associative multiplication (i.e., in a semigroup), where
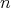 is a given positive integer regarded as an input size. Is
is a given positive integer regarded as an input size. Is
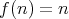 an asymptotic lower bound for the complexity of algorithms for computing
an asymptotic lower bound for the complexity of algorithms for computing
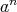 with the help of multiplications?
with the help of multiplications?
|
|
Question:
A traveler encounters a wall that extends to infinity in both directions.
There is a door in the wall, but neither the distance to it nor
the direction toward it is known to the traveler. Let the input size be the number
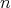 of steps
(unknown to the traveler) that initially separate the traveler from the door. Clearly, of steps
(unknown to the traveler) that initially separate the traveler from the door. Clearly,
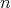 is a lower and an asymptotic lower bound for door-reaching algorithms
(in all cases, the traveler has to take
is a lower and an asymptotic lower bound for door-reaching algorithms
(in all cases, the traveler has to take 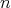 steps). Can a door-reaching algorithm with
steps). Can a door-reaching algorithm with
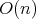 complexity bound be proposed? complexity bound be proposed?
|
|
Question:
Is it true that the function
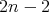 is a lower complexity bound for algorithms intended for simultaneously selecting
the largest and smallest maximal and minimal elements in an array of
length
is a lower complexity bound for algorithms intended for simultaneously selecting
the largest and smallest maximal and minimal elements in an array of
length 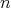 with the help of comparisons?
with the help of comparisons?
|
|
Question:
Let
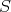 be a comparison sort algorithm and be a comparison sort algorithm and
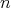 denote the number of elements in the input array. Let denote the number of elements in the input array. Let
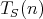 , , 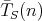 -
be the complexities of -
be the complexities of 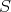 measured as the number of
comparisons in the worst and average cases, respectively. Which of the following equalities does not hold for any measured as the number of
comparisons in the worst and average cases, respectively. Which of the following equalities does not hold for any
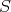 : :
|
|
Optimal algorithms in a given class are not always known. It is also possible that a given class has no optimal algorithm, i.e., an algorithm whose complexity is a lower complexity bound for algorithms in this class. |
|
|
|
Rather frequently, it is very difficult to answer whether a particular class of algorithms has one whose complexity does not grow too fast with increasing input size. |
|
|
|
For some classes of algorithms, a difficult question is whether there exists an algorithm in such a class with complexity bounded above by a polynomial whose form is not specified (such an algorithm is known as polynomial-time). |
|
|
|
In particular, many unanswered questions concern polynomial-time algorithms for decision problems, i.e., those having a yes/no solution, or a 1/0 solution, etc. In this context, we mention the well-known P≟NP problem. |
|
|
|
|
Question:
Assume that the cost of any compass-and-straightedge construction in the plane is the number of lines
(circles or straight lines) drawn in the course of the construction. Consider the problem
of constructing a segment whose length is
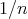 of that of the original segment, assuming that of that of the original segment, assuming that
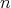 is the input size. Is there a solution algorithm whose complexity grows more
slowly than
is the input size. Is there a solution algorithm whose complexity grows more
slowly than 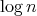 ? ?
|
|
Question:
The existence of a polynomial-time algorithm for decomposing an integer
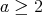 of bit length
of bit length 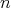 into prime factors remains
an open problem, although factorization algorithms are of great importance in cryptography.
In this context, consider the following problem: given into prime factors remains
an open problem, although factorization algorithms are of great importance in cryptography.
In this context, consider the following problem: given 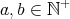 , ,
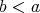 , determine whether , determine whether
 has a divisor
has a divisor  such that such that
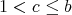 . No polynomial-time algorithm (in terms of the bit length of . No polynomial-time algorithm (in terms of the bit length of
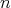 of of  )
is available for this problem. Is it true that, if such an algorithm )
is available for this problem. Is it true that, if such an algorithm 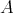 were devised, this would automatically produce a polynomial-time factorization algorithm?
were devised, this would automatically produce a polynomial-time factorization algorithm?
|
|
Question:
Is it possible to compute the product of two given complex numbers
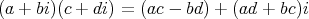 using several additions and subtractions and only three multiplications of real numbers?
(Assume that the values
using several additions and subtractions and only three multiplications of real numbers?
(Assume that the values 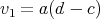 , ,
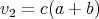 have been computed;
how can a suitable number have been computed;
how can a suitable number 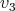 be
found using a single multiplication so that the computation of the required quantities
can be completed using only additions and subtractions?) be
found using a single multiplication so that the computation of the required quantities
can be completed using only additions and subtractions?)
|
|
Question:
Is it true that P
 NP
will be proved if we show that at least one problem in NP is in P? NP
will be proved if we show that at least one problem in NP is in P?
|
|
|
When we examine the existence of an algorithm of "not very high" complexity, an important role is played by the reducibility of one problem to another. The possibility of quickly solving some problem can imply the same possibility for a number of other problems and, on the contrary, if a certain problem cannot be quickly solved, the same can automatically be implied for a number of other problems. |
|
Considering linear reducibility, we can rigorously define the fact that one computational problem is not harder than another. |
|
|
|
Polynomial reducibility means that, if a computational problem is solvable by a polynomial-time algorithm, then another problem is also solvable by a polynomial-time algorithm. |
|
|
|
|
Question:
Is the multiplication of arbitrary square matrices linearly
reducible (see above in this section) to the multiplication of upper
triangular matrices, assuming that the latter problem is solved only by algorithms
for which
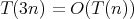 (as occurs for all reasonable algorithms designed for this problem)?
(as occurs for all reasonable algorithms designed for this problem)?
|
|
Question:
Are there problems in NP that are not NP-complete?
|
|
Question:
Imagining that there is no polynomial-time algorithm for testing
the primality of a positive integer (i.e., the AKS algorithm (see Section 9) does not exist),
would it be true that P
 NP? NP?
|
|
Along with various questions concerning the possible limits for algorithms from one or another class, always important are problems associated with complexity bounds for particular algorithms. Frequently, trivial upper and lower bounds are easy to derive, while deriving close-to-tight bounds for an algorithm requires much effort and nontrivial approaches. |
|
|
|
|
Question:
A binary algorithm for finding an element place in an ordered array of length
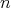 has complexity
has complexity 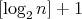 , which implies
that the complexity , which implies
that the complexity 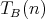 of binary insertion sort is
of binary insertion sort is
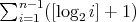 . The last
term in this sum is the largest, which yields . The last
term in this sum is the largest, which yields
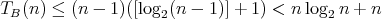 .
Is it true that .
Is it true that 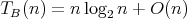 ? ?
|
|
Question:
The complexity
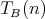 measured as the number of comparisons in binary insertion sort is
measured as the number of comparisons in binary insertion sort is
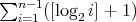 .
For some values of .
For some values of 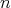 , ,
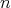 elements can be sorted using a smaller number of comparisons. Which is the smallest
elements can be sorted using a smaller number of comparisons. Which is the smallest
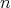 of this kind:
of this kind:
|
|
Question:
Is it true that
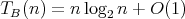 for the complexity
for the complexity 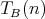 measured as the number of comparisons in the binary insertion sort as applied to an array of
measured as the number of comparisons in the binary insertion sort as applied to an array of
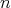 elements? (Recall that this complexity is equal to
elements? (Recall that this complexity is equal to
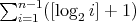 .) .)
|
|
Question:
Let
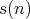 be the average number of assignments
be the average number of assignments  executed in the following algorithm for finding the smallest element of an array
executed in the following algorithm for finding the smallest element of an array
for
if od assuming that all possible relative orders of the elements in the original array of length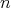 are equiprobable. Which of the following assertions is true:
are equiprobable. Which of the following assertions is true:
|
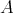 is considered from the point of view of complexity, it is assumed that, at its possible inputs
is considered from the point of view of complexity, it is assumed that, at its possible inputs
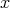 , we are given the nonnegative integer function
, we are given the nonnegative integer function
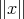 ,
which is known as the input size,
and nonnegative integer time and space cost functions
,
which is known as the input size,
and nonnegative integer time and space cost functions
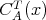 ,
,
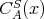 (space cost is also known as memory storage cost; the cost required for storing the input itself is ignored).
(space cost is also known as memory storage cost; the cost required for storing the input itself is ignored).
 are
functions of numerical argument defined as
are
functions of numerical argument defined as
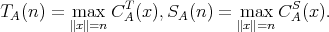
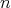 , the corresponding inputs form a finite set
, the corresponding inputs form a finite set
 .
Assume that each
.
Assume that each 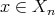 is assigned some probability
is assigned some probability 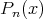 :
:
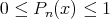 and
and
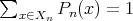 . Thus, the time and space cost functions
. Thus, the time and space cost functions
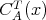 and
and 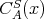 of an algorithm
of an algorithm
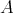 on inputs
on inputs
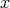 of size
of size 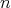 are random variables on
are random variables on 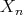 .
The average-case time and space complexities of
.
The average-case time and space complexities of 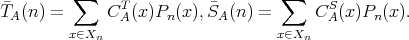
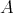 for any probability distribution on the set
for any probability distribution on the set
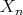 , the average-case complexity
does not exceed the worst-case complexity:
, the average-case complexity
does not exceed the worst-case complexity:
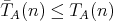 ,
,
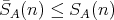 .
.
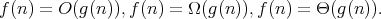
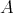 and
and
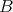 have respective complexities
have respective complexities
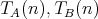 such that
such that
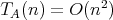 ,
,
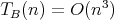 , it cannot be concluded that
, it cannot be concluded that
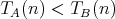 for all sufficiently large
for all sufficiently large 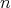 .
.