БАЛАНСОВАЯ ДИНАМИЧЕСКАЯ НОРМАТИВНАЯ МОДЕЛЬ

ОЦЕНКИ ИННОВАЦИОННОГО ПОТЕНЦИАЛА КИРОВСКОЙ ОБЛАСТИ

 

Оленев Н.Н.

 

Вычислительный центр им. А.А. Дородницына Российской академии наук, Россия, 119991, г. Москва, ул. Вавилова 40, (495)1373974, (495)1356159, olenev@ccas.ru

 

 

1. Региональные модели оценки инновационного потенциала

Статистические данные, собираемые для оценки инновационного потенциала региона, как правило, несогласованны, и для их согласования нужно использовать какую-либо модель. Кроме того, догоняющему региону можно осуществлять идеи, созданные в других регионах страны и мира и тут сбор данных о наличии своих собственных разработок не поможет в оценке совокупного инновационного потенциала. А вот имитационная модель региональной экономики дает возможность получить количественную оценку динамики макропоказателей экономики региона, включая оценку показателей инновационного потенциала, главными из которых являются показатели структуры человеческого капитала и его динамики. Так и была обоснована Концепция использования имитационной модели экономики региона для исследования его инновационного потенциала, выдвинутая в [1].

Рассмотрим следующую триаду многосекторных математических моделей региональной экономики, которые можно использовать для практической оценки инновационного потенциала и его динамики. Самой известной и наиболее часто используемой моделью является межотраслевой баланс В.В. Леонтьева [2], или модель ╚затраты-выпуск╩. Эта модель оказала всестороннее влияние на умы и практические действия лиц, принимающих решения. Статистические ведомства всех стран мира собирают данные, необходимые для составления межотраслевого баланса. В случае Кировской области трудно воспользоваться такой моделью по следующим основным причинам. Во-первых, экономика регионов является чрезвычайно открытой и поэтому региональные статистические ведомства не собирают данные, необходимые для построения межотраслевого баланса региона, а собирают только данные для построения межотраслевого баланса всей страны. Во вторых, в условиях трансформационных изменений в экономике леонтьевские коэффициенты (прямые нормы затрат продукции смежных отраслей на выпуск продукции отрасли) быстро меняются от году к году. Кроме того, межотраслевой баланс по природе своей является статическим, поскольку строится на основе данных целого года, и рассмотрение динамических версий его несколько искусственно.

Второй тип моделей основан на выделении экономических агентов, приписывании им определенных целей, составлении сложившейся иерархической структуры агентов на всех рассматриваемых рынках и решении соответствующей иерархии оптимизационных задач. Такой тип динамических региональных моделей успешно строится, например, в отделе ╚Математическое моделирование экономических систем╩ Вычислительного центра им. А.А. Дородницына Российской академии наук. [3], который возглавляет академик А.А. Петров. На построение каждой новой модели уходит до года работы коллектива ученых из десяти человек. Экономическая ситуация в стране с переходной экономикой может кардинально измениться и в течение года, поэтому для поддержания такого рода моделей в действующем состоянии нужно постоянно держать команду высококвалифицированных исследователей. Регионов в России в настоящее время 89, всем хочется уметь анализировать текущее состояние экономики и делать обоснованные прогнозы возможного развития.

Положение могут спасти модели третьего типа: многосекторные балансовые нормативные динамические модели с запасами продуктов и финансовых средств. Такие модели занимают промежуточное положение между моделями первых двух типов и до сих пор не использовались в практике аналитических и прогнозных расчетов только в силу огромного числа неизвестных параметров, которые нельзя определить напрямую из данных экономической статистики. Но появление высокоскоростной вычислительной техники создает предпосылки для использования таких моделей, если разработать специальную процедуру идентификации их параметров, что и предлагает настоящая работа.

 

2. Описание трехсекторной модели экономики Кировской области

Выделим восемь экономических агентов: Производителей, которые в модели представлены тремя секторами экономики Кировской области (X, Y, Z), Домашние хозяйства (L), Правительство региона (G), Банковскую систему региона (B). Для замыкания описаний вводится также Торговый посредник (T) и Внешний рынок (O). Три сектора в модели экономики Кировской области представлены лесопромышленным комплексом X, комплексом новых отраслей в биотехнологии и химии Y, комплексом оставшихся отраслей экономики региона Z. Модель описывает динамику материальных и финансовых балансов через изменение запасов продуктов, факторов производства и денег. При описании модели учитывается налогообложение производителей и домашних хозяйств и теневой оборот в сфере производства и потребления. Производители поставляют продукцию на внутренние и внешние рынки, а также на рынки промежуточной продукции смежных отраслей. Домашние хозяйства предлагают труд и потребляют конечную продукцию. Банковская система выпускает денежные средства и выдает кредиты производителям. Правительство региона собирает налоги (налог на прибыль n1, налог на добавленную стоимость n2, акцизы n3, единый социальный налог n4, таможенные пошлины на экспорт n5, таможенные пошлины на импорт n6, подоходный налог n7) и распределяет полученные средства. Модель учитывает теневой оборот, который не облагается налогами.

Будем использовать стандартные обозначения, близкие к обозначениям системы построения и анализа моделей экономики ЭКОМОД [4], разработанной профессором И.Г. Поспеловым и его учениками. В этих обозначениях показатели и параметры модели снабжены верхними и нижними индексами, причем верхние индексы используются для агентов, а нижние для благ. Одни и те же символы латиницы могут использоваться для обозначения верхних индексов, нижних индексов и самих показателей (или параметров) и при этом обозначать разные вещи. Интенсивные показатели и параметры будем обозначены строчными символами, а экстенсивные показатели и именованные индексы √ прописными. Верхний индекс, например, n, будем использовать для указания агентов: X, Y, Z, L, G, B, T, O, а если верхних индексов два, то они означают передачу блага или денег от агента, указанного левым индексом, к агенту, указанному правым индексом. Нижний индекс будем использовать для пяти благ: трех продуктов секторов i = X, Y, Z и двух факторов производства √ труда L и капитала K. Считаем, что распределение запаса каждого блага производится по нормативу: ainm - доля запаса блага i агента n, идущая к агенту m (ainn = ain). Считаем, что распределение денег производится также по некоторому нормативу: bimn - доля запаса денег агента m, идущая агенту n за продукт i (binn = bin). Коэффициенты фондоемкости также задаются нормативами: cim √ норма затрат продукта i на создание единицы фондообразующего продукта агента m. Параметры производственных функций секторов заданы константами.

Для получения представления о динамике показателей у Производителей рассмотрим описание сектора X (эквивалентные названия: лесопромышленный комплекс Кировской области, экономический агент X). Будем считать, что в каждый момент времени t выпуск агентом X продукта YX(t) задается степенной производственной функцией типа Кобба-Дугласа от используемых факторов производства: труда L, капитала K, промежуточных продуктов смежных секторов Y и Z.

 

, ═════════════════════════ (1)

 

где . Здесь и далее, если не оговорено противное, все показатели, как здесь YX(t), QLX(t), QKX(t), QYX(t), QZX(t), считаются функциями времени t, поэтому этот аргумент для сокращения записи в формулах опускается. Все параметры, как правило, считаются константами, как здесь aLX, aKX, aYX, aZX, δLX, δKX, δYX, δZX Î (0, 1). Производство открытого X и теневого V продукта агентом X осуществляется на общих фондах, общих трудовых ресурсах и общих запасах промежуточных продуктов, а произведенная продукция (выпуск) YX(t) делится в заданной пропорции (1 √ qX) : qX═ на открытый (╚белый╩) выпуск X и теневой (╚черный╩) выпуск V, где qX √ доля тени в общем выпуске продукта YX(t). Теневой продукт используется для продажи населению, другим секторам и внешним агентам. Предполагаем, что инвестиции могут быть только легальными. Запас своего открытого продукта QXX(t) растет за счет выпуска и убывает за счет отгрузки агентам Y, Z, L ═(отгружает посреднику по нормативу) и себе для инвестиций IX(t). Считаем, что расходы на освоение инвестиций от своего продукта совпадают с доходами от них (вклад собственных средств на инвестиции за счет продукции сектора не учитываем в его валовом выпуске). На внешний рынок идет заданная доля запаса своего продукта XXXO(t).

 

, ═════ ═══════════ ═══════════

 

,══ ,══ .══════════ (2)

 

Запас промежуточного продукта Y у агента X растет за счет покупки открытого продукта Y у агента Y (сектора биотехнологий Кировской области) по цене pYX(t) и теневого продукта W у агента Y по цене pWX(t) и убывает за счет использования его в производстве в качестве сырья и инвестиций. Запас промежуточного продукта Z у агента X растет за счет покупки открытого продукта у агента Z (прочих отраслей Кировской области) по цене pZX(t) и теневого продукта U у агента Z по цене pUX(t) и убывает за счет использования его в производстве в качестве сырья и инвестиций

 

, .═ ═(3)

 

Запас труда в секторе X прирастает за счет покупки у агента L (домашних хозяйств Кировской области) открытого труда L по официальной ставке заработной платы sLX(t) и теневого труда B по теневой ставке sBX(t) и убывает в силу спроса на труд агента X.

 

. ════════════════════════════════════════ (4)

 

Запас капитала в секторе X прирастает за счет инвестиций bKXWX(t), а убывает в силу амортизации капитала у агента X с темпом μKX и использования капитала в производстве в секторе X.

 

.════════════════════════════════════════════ (5)

 

Считаем, что агент X берет весь предлагаемый агентом B (банковской системой Кировской области) кредит, однако объем предоставляемого кредита CBX(t) ограничен ликвидационной стоимостью производственных фондов, которая считается пропорциональной запасу капитала.

 

,══ sX > 0. ════════ ═══════════════════════════════════ ═══════════ ═(6)

 

Задолженность ZX(t) агента X банковской системе B прирастает за счет выдачи новых кредитов CBX(t) и начисления текущего процента по кредитам r(t) на имеющуюся задолженность, а уменьшается в силу платежей погашения HXB(t).

 

,══ ═════════════ ═══════════ ═(7)

 

Запас открытых (╚белых╩) денег у агента X прирастает при поступлении кредитов, при продаже товара на внешнем рынке и на внутренних рынках, за счет трансфертов сектору X из областного консолидированного бюджета TGX(t) и поступлений ╚отмытых╩ денег из теневого оборота bBXBX(t). Он уменьшается при оплате труда L, промежуточного потребления смежных секторов Y и Z, платежах погашения кредитов и перечислениях налогов в консолидированный бюджет.

 

═══════════════════════════

═══════════ ,══════ (8)

 

где w(t) √ рублевый курс доллара, а трансфертные платежи в консолидированный бюджет равны сумме налоговых отчислений минус трансферты из бюджета TGX(t) (возврат НДС + субсидии и пр.).

Отчисления в консолидированный бюджет агента X (лесопромышленного комплекса Кировской области) TXG(t) складываются из отчислений по налогу на прибыль T1XG(t), налогу на добавленную стоимость T2XG(t), акцизам T3XG(t), единому социальному налогу T4XG(t), таможенным платежам на экспорт T5XG(t).

 

,═════════════════════════════════════════════════════════════

 

,══ ,═══════════════════════════════════════════════════════════════════════

 

, ════════════════════════════════

 

══════════════════════════════════════

,═════════════════════════════════════

 

. ═══════════════════════════════════════════════

,══════════════════ (9)

 

Запас QVX(t) теневого продукта V в секторе X прирастает за счет производства и убывает за счет поставок домашним хозяйствам и смежным отраслям.

 

.════════════ ═══════════════════════ (10)

 

Запас теневых денег прирастает при продаже теневого продукта, как конечного,-- населению L и,- как промежуточного, смежным секторам Y и Z, часть bBX запаса теневых денег успевают отмыть, часть bBXG ═попадает в качестве штрафных санкций в доходную часть консолидированного бюджета правительства, а часть bBXL поступает населению в качестве теневых доходов.

 

.════════════ (11)

 

Аналогичным образом в модели описана динамика показателей секторов Y и Z, за тем исключением, что для сектора биотехнологий Y предполагается повышенная отдача факторов производства: 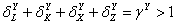, - поскольку этот сектор включает инновационные отрасли, в частности, науку и образование.

Экономический агент T (торговый посредник) в модели играет роль чистого посредника, не получающего доходов и потому не имеющего ответственности по налогам. Описание этого агента введено для описания региональных рынков продукции, на которых определяются внутренние цены на все продукты. Считаем, что изменение цен обратно пропорционально изменению запасов соответствующих продуктов. Например, Изменение запаса QYL(t) конечного продукта Y сектора биотехнологий Кировской области, распространяемого по легальному каналу сбыта и предназначенного агенту L (домашним хозяйствам области), у посредника T определяет изменение индекса потребительских цен pYL на легальную продукцию Y сектора биотехнологий.

 

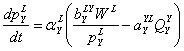,══ .══════════════════ (12)

 

В описании агента L (домашних хозяйств Кировской области) определяется уровень безработицы в составе экономически активного населения Кировской области, дифференцированный по секторам производства X, Y, Z. Внутри секторов безработные подразделены на безработных в открытой части экономики и безработных теневой части экономики. Безработица увеличивается, если предложения труда превышает спрос на него и уменьшается в противном случае.

Считаем, что рост открытых и теневых ставок заработной платы в секторах может происходить как при нехватке кадров, так и при росте потребительских цен на соответствующую продукцию сектора.

Например, открытая sZL(t) и теневая sZB(t) ставки заработной платы в секторе Z (прочих отраслей Кировской области) меняются в силу уравнений

 

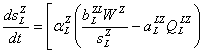
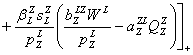,═ ═,══ (13)

 

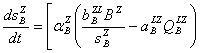
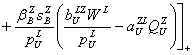, ══.═ ═(14)

 

Отчисления в консолидированный бюджет агента L (домашних хозяйств Кировской области) TLG(t) складываются из отчислений по таможенным платежам на импорт T6LG(t) и отчислений по подоходному налогу T7LG(t) с открытой части дохода.

 

,══ ,══ .══ (15)

 

В модели считается, что все деньги у домашних хозяйств являются открытыми независимо от источника их поступления.

 

══════════════

.══════════════ (16)

 

Банковская система Кировской области не является замкнутой, большую роль в инвестиционных решениях играют филиалы Российских банков других регионов. Поэтому в качестве первого приближения при описании банковской системы Кировской области предполагалось, что часть золотовалютных резервов Российской федерации обеспечивают резервирование активов Кировской области.

Итак, считаем, что банковские активы областной банковской системы состоят из золото-валютных резервов R(t) и суммарной задолженности секторов Z(t), а пассивы √ из суммарных запасов денег у контрагентов банковской системы W(t), которые подчиняются финансовому балансу банковской системы:

 

═wR(t) + Z(t) = W(t),══════════════════════════════════════════════════ (17)

 

где w(t) √ курс обмена иностранной валюты на отечественную определяется как заданная функция времени, рублей за один доллар. Срочные депозиты, на которые начисляют процент не учитываем. Золото-валютные резервы R(t) (в млрд долларов США) определяются платежным балансом

 

═, ══.════ ════════════ (18)

 

Здесь piO √ цена на экспортный товар XiiO сектора i на внешнем рынке (в остальном мире O), в долларах за единицу. Рассматриваем весь импорт как отдельный потребительский товар, доля которого bMLO в потреблении населения фиксирована. Внешние заимствования и перетоки капитала через границу в (18) не учтены.

Суммарная задолженность агентов Z(t) растет за счет выдачи новых кредитов CBi, начисления процентов на остаток задолженности и снижается за счет погашения задолженности

 

,══ (или Z = ZX + ZY+ ZZ). ════════ (19)

 

Банковская прибыль

 

dBL = r(t)Z(t)══════════════════════════════════════════════════════════════ (20)

 

поступает в доходы населения. Суммарные запасы денег

 

. ════════════════════════════ (21)

 

Резервы банковской системы wR(t) обеспечивают вклады контрагентов при законодательно установленной норме резервирования x.

 

.══════════════════════════════════════════════════════════ (22)

 

Полная модель содержит порядка ста соотношений и более восьмидесяти параметров, которые невозможно определить напрямую из данных статистики. Казалось бы, подобного типа нормативные модели совершенно бессмысленны, поскольку для проведения осмысленных качественных и количественных расчетов на них необходимо провести идентификацию их внешних параметров, а большая часть параметров не может быть оценена напрямую из данных экономической статистики.

Предложена новая технология идентификации внешних параметров модели, основанная на использовании высокоскоростных параллельных вычислениях на многопроцессорной системе [5]. Для идентификации параметров сравниваются полученные при расчетах на модели временные ряды макропоказателей экономики региона с соответствующими статистическими временными рядами. В качестве критериев близости временных рядов использован индекс несовпадения Тейла [6] и недавно построенный на основе вейвлет коэффициентов критерий похожести нелинейных временных рядов [7].

Критерием качества идентификации параметров модели является количественное соответствие основных макроэкономических показателей статистическим показателям экономики региона за период с начала 1999 года и до конца 2005 года [5]. Проведены пробные вычислительные эксперименты, показавшие работоспособность модели

Работа выполнена в рамках государственного контракта 02.449.11.7026 ╚Исследование инновационного потенциала Кировской области с целью создания центров трансфера технологий╩, при финансовой поддержке Российского фонда фундаментальных исследований (коды проектов 04-07-90346, 04-01-00606), при поддержке программы фундаментальных исследований Президиума РАН ╧15, при финансовой поддержке Российского гуманитарного научного фонда (код проекта 06-02-91821 а/G),. по гранту Президента РФ по государственной поддержке ведущих научных школ (код проекта НШ-5379.2006.1).

 

 

Литература

1.      Оленев Н.Н., Шатров А.В. Концепция использования имитационной модели экономики региона для исследования его инновационного потенциала. // Математическое моделирование развивающейся экономики: Сб. тр. летней школы по экономико-математическому моделированию ЭКОМОД-2006. √ Киров: Изд-во ВятГУ, 2006. √ 152 с. С. 10-24.

2.      Обросова Н.К., Оленев Н.Н. Математические модели в экономике. Методическое пособие по практической работе. М.: Изд-во РУДН. 2004.- 44 с. [Электронная версия пособия http://www.ccas.ru/mmes/educat/lab05/]

3.      Автухович Э.В., Гуриев С.М., Оленев Н.Н., Петров А.А., Поспелов И.Г., Шананин А.А., Чуканов С.В. Математическая модель экономики переходного периода═ // Вычислительный центр РАН, М. 1999. 143с. [http://www.ccas.ru/olenev/book1.pdf]

4.      Завриев Н.К., Поспелов И.Г., Поспелова Л.Я., Хохлов М.А. Уроки эксплуатации системы ЭКОМОД и новые перспективы. М.: ВЦ РАН, 2004. 72 с.

5.      Оленев Н.Н. Основы параллельного программирования в системе MPI. М.: ВЦ РАН. 2005. 80 с.

6.      Тейл Г. Экономические прогнозы и принятие решений. М.: Статистика, 1971. 488 с.

7.      Бурнаев Е.В., Оленев Н.Н. Меры близости на основе вейвлет коэффициентов для сравнения статистических и расчетных временных рядов // Межвузовский сборник научных и научно-методических трудов за 2005 год (Десятый выпуск). Киров: Изд-во ВятГУ, 2006. C. 41-51.

 

Олен╦в Николай Николаевич, 1959 г.р., окончил Московский физико-технический институт (1982), аспирантуру ВЦ АН СССР (1987), к.ф.-м.н. (1993), доцент (2005), старший научный сотрудник ВЦ РАН, доцент МФТИ(ГУ), РУДН и ВятГУ, - краткая биография выбрана Marquis Who's Who для размещения в энциклопедии Who's Who in Science and Engineering, 2006-2007