Меры близости на основе вейвлет коэффициентов для сравнения статистических и расчетных временных рядов
Е.В. Бурнаев1, Н.Н. Оленев2
1Московский Физико-Технический Институт (Государственный Университет), Институтский переулок д.9, ═г. Долгопрудный, Московская область, Россия 141700,
2Вычислительный центр им. А.А. Дородницина РАН, ул. Вавилова д.40, Москва ГСП-1, Россия 119991,
WWW home page: http://www.ccas.ru/olenev/
Введение
Мера близости между данными является центральным понятием большинства алгоритмов для поиска знаний в базах данных (data mining algorithms). Также мера близости необходима при идентификации макроэкономической модели для сравнения статистических и расчетных временных рядов. В данном контексте временные ряды считаются близкими, если они близки как функции времени (другими словами, между значениями временных рядов существует сильная, возможно нелинейная, связь). Для ⌠сложных■ данных, таких как, например, финансовые ═или макроэкономические временные ряды, обычная мера близости типа евклидова расстояния, зачастую не применима. На рисунке 1 изображены обменные курсы South Africa rand и Switzerland franc по отношению к US dollar с 01.01.90 по 29.10.93, 1000 отсч╦тов. Ясно, что подсчитанное для этих рядов евклидово расстояние значительно, хотя, если удалить тренд и провести подходящее масштабирование по оси ординат, окажется, что эти временные ряды имеют схожее поведение (рисунок 2), при этом евклидово расстояние значительно уменьшается.
Из вышеприведенного примера ясно, что меру близости временного ряда следует рассчитывать на основе некоторых характеристик временного ряда, а не на основе значений ряда. Причем эти характеристики должны быть робастны по отношению к наличию тренда, изменениям в уровне и масштабе ряда. Также, в случае применения мер близости в алгоритмах поиска схожих временных рядов в больших базах данных, характеристики должны рассчитываться сравнительно быстро. В работе предлагаются меры близости для временных рядов на основе вейвлет коэффициентов, рассчитываемых с помощью дискретного вейвлет преобразования за линейное время, и обладающих вышеперечисленными свойствами.
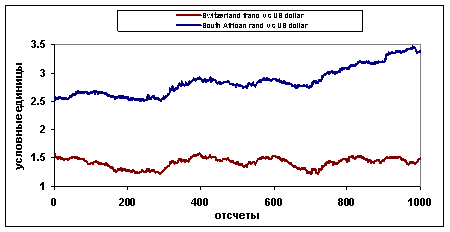
Рис.1. Обменные курсы South Africa rand и Switzerland franc по отношению к US dollar с 01.01.90 по 29.10.93, 1000 отсч╦тов.
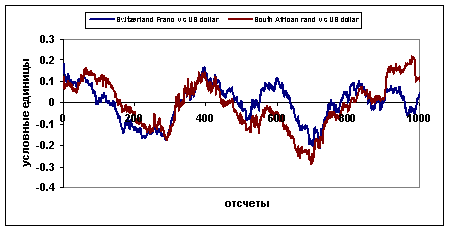
Рис.2. Обменные курсы South Africa rand и Switzerland franc по отношению к US dollar с 01.01.90 по 29.10.93, 1000 отсч╦тов с вычетом тренда и подходящим масштабированием по оси ординат.
Дискретное вейвлет преобразование и его свойства
Пусть
![]() ═-
временной ряд длины
═-
временной ряд длины ![]() ═для некоторого целого
═для некоторого целого ![]() ,
, ![]() ═-
максимальный масштаб,
═-
максимальный масштаб, ![]() ═- вейвлет фильтр длины
═- вейвлет фильтр длины ![]() , а
, а ![]() ═-
масштабный фильтр длины
═-
масштабный фильтр длины ![]() . Не всегда найдется целое
. Не всегда найдется целое ![]() , такое, что
, такое, что
![]() . Это
ограничение можно снять, дополняя временной ряд нулями или значениями, равными
среднему ряда
. Это
ограничение можно снять, дополняя временной ряд нулями или значениями, равными
среднему ряда ![]() , до тех пор, пока не будет выполнено
условие
, до тех пор, пока не будет выполнено
условие ![]() ═для
некоторого целого
═для
некоторого целого ![]() ═[6]. Пример вейвлет и масштабного
фильтров приведен в приложении. Заметим, что вейвлет и масштабный фильтры
играют роли высокочастотного и низкочастотного фильтров соответственно [3], [5].
═[6]. Пример вейвлет и масштабного
фильтров приведен в приложении. Заметим, что вейвлет и масштабный фильтры
играют роли высокочастотного и низкочастотного фильтров соответственно [3], [5].
Положим ![]() ═
═![]() . Тогда на масштабе
. Тогда на масштабе ![]() ═будет ровно
═будет ровно ![]() ═масштабных
и вейвлет коэффициентов
═масштабных
и вейвлет коэффициентов ![]() ═и
═и ![]() ═
═![]() ═соответственно, которые вычисляются
на основе масштабных коэффициентов
═соответственно, которые вычисляются
на основе масштабных коэффициентов ![]() ═
═![]() ═предыдущего масштаба
═предыдущего масштаба ![]() ═по формулам
дискретного вейвлет преобразования [3]
═по формулам
дискретного вейвлет преобразования [3]
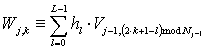 ═и
═и 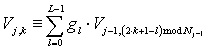 .
.
При
этом операция типа ![]() ═для целых
═для целых ![]() ═и
═и ![]() ═определяется
следующим образом. Если
═определяется
следующим образом. Если ![]() , то
, то ![]() ; если
; если ![]() ═- любое другое целое
число, то
═- любое другое целое
число, то ![]() , где целое
, где целое ![]() ═подобрано так, чтобы
═подобрано так, чтобы ![]() . В приложении приведен алгоритм для
рекурсивного вычисления вейвлет и масштабных коэффициентов по
. В приложении приведен алгоритм для
рекурсивного вычисления вейвлет и масштабных коэффициентов по ![]() ═
═![]() . Набор
коэффициентов
. Набор
коэффициентов ![]() ═
═![]() ═при
═при ![]() ═и
═и ![]() ═
═![]() ═составляет
дискретное вейвлет разложение. По этим коэффициентам с помощью обратного
вейвлет преобразования можно однозначно восстановить временной ряд [3], причем
выполняется равенство типа равенства Парсеваля
═составляет
дискретное вейвлет разложение. По этим коэффициентам с помощью обратного
вейвлет преобразования можно однозначно восстановить временной ряд [3], причем
выполняется равенство типа равенства Парсеваля ![]() .
.
Пусть ![]() , тогда на масштабе
, тогда на масштабе ![]() ═будет всего один
масштабный коэффициент
═будет всего один
масштабный коэффициент ![]() , пропорциональный среднему ряда
, пропорциональный среднему ряда ![]() . Если
обнулить
. Если
обнулить ![]() ,
все остальные вейвлет коэффициенты оставить без изменений и сделать обратное
вейвлет преобразование, то результат будет такой же, как если бы из ряда
,
все остальные вейвлет коэффициенты оставить без изменений и сделать обратное
вейвлет преобразование, то результат будет такой же, как если бы из ряда ![]() ═вычли
полиномиальный тренд степени
═вычли
полиномиальный тренд степени ![]() ═[6].
═[6].
Коэффициент ![]() ═пропорционален разности смежных
взвешенных средних длины
═пропорционален разности смежных
взвешенных средних длины ![]() , то есть указывает на изменение средних
значений ряда на временном масштабе
, то есть указывает на изменение средних
значений ряда на временном масштабе ![]() . Значение
. Значение ![]() ═показывает, сколько энергии
ряда
═показывает, сколько энергии
ряда ![]() ═содержится
в отрезке частот
═содержится
в отрезке частот ![]() ═в момент времени
═в момент времени ![]() . Для широкого класса
стохастических процессов величины
. Для широкого класса
стохастических процессов величины ![]() ═независимы, и распределены как
═независимы, и распределены как ![]() , где
, где ![]() ═- некоторая
константа [3].
═- некоторая
константа [3].
Коэффициент ![]() ═пропорционален взвешенному среднему
длины
═пропорционален взвешенному среднему
длины ![]() ,
то есть указывает на среднее значение ряда на временном масштабе
,
то есть указывает на среднее значение ряда на временном масштабе ![]() . Значение
. Значение ![]() ═показывает,
сколько энергии ряда
═показывает,
сколько энергии ряда ![]() ═содержится в отрезке частот
═содержится в отрезке частот ![]() ═в момент
времени
═в момент
времени ![]() .
.
В формулах для подсчета набора вейвлет и масштабных коэффициентов
неявно делается предположение о возможности циклического продолжения ряда ![]() , то есть,
что выполняется равенство
, то есть,
что выполняется равенство ![]() . Если это не так, то значения ⌠граничных■
вейвлет коэффициентов
. Если это не так, то значения ⌠граничных■
вейвлет коэффициентов ![]() ═для
═для ![]() ,
, ![]() ═будут завышены (
═будут завышены (![]() - целая
часть числа
- целая
часть числа ![]() ). При расчетах мер близости между
временными рядами эти ⌠граничные■ вейвлет коэффициенты не будут приниматься во
внимание.
). При расчетах мер близости между
временными рядами эти ⌠граничные■ вейвлет коэффициенты не будут приниматься во
внимание.
Будем использовать вейвлет и масштабные фильтры Добеши с ![]() ═(см.
приложение). В этом случае
═(см.
приложение). В этом случае ![]() ═не чувствительны к линейному тренду, то
есть если ряд
═не чувствительны к линейному тренду, то
есть если ряд ![]() ═суть значения некоторой линейной
функции, то
═суть значения некоторой линейной
функции, то ![]() .
.
Для фильтров Добеши с ![]() ═⌠граничными■ коэффициентами являются
коэффициенты
═⌠граничными■ коэффициентами являются
коэффициенты ![]() ,
, ![]() ═и
═и ![]()
![]() ═[6]. При расчетах
рекомендуется использовать именно эти фильтры, поскольку в таком случае
количество ⌠граничных■ коэффициентов будет минимальным.
═[6]. При расчетах
рекомендуется использовать именно эти фильтры, поскольку в таком случае
количество ⌠граничных■ коэффициентов будет минимальным.
Алгоритм подсчета меры близости между временными рядами
- Пусть
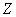 ═-
временной ряд длины
═-
временной ряд длины 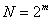 ═для некоторого целого
═для некоторого целого 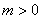 ═(если
необходимо, ряд дополняется нулями или значениями, равными среднему ряда,
пока═ длина ряда не будет равна степени двойки). Используя фильтр Добеши с
═(если
необходимо, ряд дополняется нулями или значениями, равными среднему ряда,
пока═ длина ряда не будет равна степени двойки). Используя фильтр Добеши с
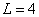 ,
подсчитываем вейвлет коэффициенты
,
подсчитываем вейвлет коэффициенты 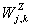 ═
═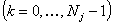 ═для
═для 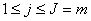 ═(см.
приложение). Общее количество вейвлет коэффициентов равно
═(см.
приложение). Общее количество вейвлет коэффициентов равно 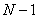 .
. - Выкидываем
⌠граничные■ вейвлет коэффициенты. Пусть
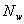 ═- количество оставшихся
вейвлет коэффициентов. Очевидно, что для фильтров Добеши с
═- количество оставшихся
вейвлет коэффициентов. Очевидно, что для фильтров Добеши с 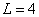 ═
═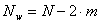 . Если
временной ряд дополнялся нулями или значениями, равными среднему ряда, то выкидываем
также те вейвлет коэффициенты, при подсчете которых использовались эти ⌠новые■
значения временного ряда. При этом
. Если
временной ряд дополнялся нулями или значениями, равными среднему ряда, то выкидываем
также те вейвлет коэффициенты, при подсчете которых использовались эти ⌠новые■
значения временного ряда. При этом 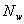 ═уменьшается.
═уменьшается. - Положим
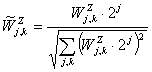 ═для
оставшихся после выкидывания вейвлет коэффициентов
═для
оставшихся после выкидывания вейвлет коэффициентов 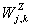 . Вектор
коэффициентов
. Вектор
коэффициентов 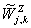 ═представляет собой характеристики
ряда, которые, как следует из вышеприведенных свойств вейвлет коэффициентов,
1) робастны по отношению к изменению среднего ряда, тренду,
масштабированию, 2) независимы и нормально распределены с нулевым средним
и постоянной дисперсией.
═представляет собой характеристики
ряда, которые, как следует из вышеприведенных свойств вейвлет коэффициентов,
1) робастны по отношению к изменению среднего ряда, тренду,
масштабированию, 2) независимы и нормально распределены с нулевым средним
и постоянной дисперсией. - Пусть
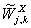 ═и
═и
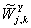 ═-
вектора характеристик временных рядов
═-
вектора характеристик временных рядов 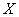 ═и
═и 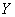 ═соответственно
(предполагается, что ряды
═соответственно
(предполагается, что ряды 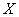 ═и
═и 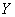 имеют одинаковую длину).
В качестве меры близости между временными рядами ═
имеют одинаковую длину).
В качестве меры близости между временными рядами ═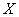 ═и
═и 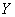 ═можно
использовать косинус угла между векторами характеристик, а именно
═можно
использовать косинус угла между векторами характеристик, а именно 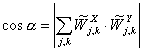 . ═Положим
. ═Положим
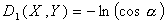 ═и
═и
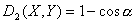 .
Такое преобразование упрощает интерпретацию значений
.
Такое преобразование упрощает интерпретацию значений 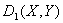 ═и
═и 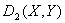 ═-
теперь ⌠дал╦ким■ объектам соответствуют большие значения этих мер
близости, и наоборот.
═-
теперь ⌠дал╦ким■ объектам соответствуют большие значения этих мер
близости, и наоборот. - Поскольку
коэффициент
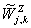 ═характеризует изменение в
значениях ряда
═характеризует изменение в
значениях ряда 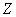 ═на определенном масштабе в
определенный момент времени, то имеет смысл определить меры близости на
основе значения
═на определенном масштабе в
определенный момент времени, то имеет смысл определить меры близости на
основе значения 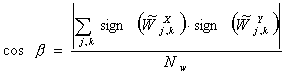 . Положим
. Положим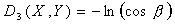 и
и 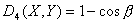 .
Преимущество
.
Преимущество 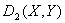 ═и
═и 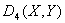 ═в том, что эти меры
близости ограничены. Качественной разницы между мерами близости
═в том, что эти меры
близости ограничены. Качественной разницы между мерами близости 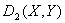 ,
, 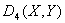 ═и
═и 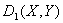 ,
, 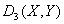 ═нет.
═нет.
Введенные меры близости ![]() ═и
═и ![]() ═характеризуют,
насколько сильна нелинейная зависимость между временными рядами
═характеризуют,
насколько сильна нелинейная зависимость между временными рядами ![]() ═и
═и ![]() ═(другими
словами, меры близости
═(другими
словами, меры близости ![]() ═и
═и ![]() ═показывают, насколько
колебания временных рядов
═показывают, насколько
колебания временных рядов ![]() ═и
═и ![]() ═по отношению к их линейным
трендам схожи). Поскольку вектор характеристик может моделироваться как
случайный вектор, имеющий нормальное распределение с диагональной
ковариационной матрицей и нулевым средним, то значениям мер близости
═по отношению к их линейным
трендам схожи). Поскольку вектор характеристик может моделироваться как
случайный вектор, имеющий нормальное распределение с диагональной
ковариационной матрицей и нулевым средним, то значениям мер близости ![]() ═и
═и ![]() ═можно поставить
в соответствие некоторые уровни значимости. Значения мер близости
═можно поставить
в соответствие некоторые уровни значимости. Значения мер близости ![]() ═и
═и ![]() ═показывают,
насколько направления колебаний временных рядов
═показывают,
насколько направления колебаний временных рядов ![]() ═и
═и ![]() ═по отношению к их
линейным трендам схожи.
═по отношению к их
линейным трендам схожи.
Заметим, что поскольку дискретное вейвлет преобразование с фильтрами Добеши не инвариантно по отношению к обращению времени, то значения введенных мер близости изменятся при одновременном обращении времени у обоих временных рядов. Тем не менее, если для двух временных рядов меры близости принимали близкие к нулю значения, то после обращения времени═ они по-прежнему будут принимать близкие к нулю значения.
Тестирование мер близости
Для тестирования введенных мер близости использовались ряды
обменных курсов 30 валют по отношению к US dollar, взятые
с сайта Federal Reserve Statistical Release, USA c 26.02.91 по 31.12.98, 2048 отсчетов (www.federalreserve.gov/releases/h10/hist/default1999.htm). В таблице 1 приведены
значения мер близости ![]() ═и
═и ![]() ═между курсом Switzerland
franc и остальными обменными курсами. Также в таблице приведены
результаты разбиения рядов на 10 кластеров с помощью алгоритма k-Means [4] (в столбцах указаны номера кластеров, к
которым принадлежат ряды). При разбиении на кластеры использовались два типа
расстояния между рядами:
═между курсом Switzerland
franc и остальными обменными курсами. Также в таблице приведены
результаты разбиения рядов на 10 кластеров с помощью алгоритма k-Means [4] (в столбцах указаны номера кластеров, к
которым принадлежат ряды). При разбиении на кластеры использовались два типа
расстояния между рядами: ![]() ═√ на основе косинуса угла и
═√ на основе косинуса угла и ![]() ═√ на основе
коэффициента корреляции между рядами. Например, для рядов
═√ на основе
коэффициента корреляции между рядами. Например, для рядов ![]() ═и
═и ![]() ═расстояние
на основе косинуса равно
═расстояние
на основе косинуса равно 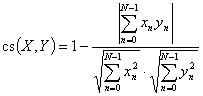 , а на основе коэффициента корреляции равно
, а на основе коэффициента корреляции равно
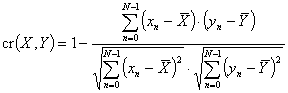 .
.
Из таблицы 1 можно заметить, что между введенными мерами близости и разбиением на кластеры, по крайней мере, для первых 10 обменных курсов, существует разумное соответствие.
На рисунках 3 и 4 изображена зависимость мер близости ![]() ═и
═и ![]() ═между обменными
курсами Switzerland franc и Australia dollar, Austria schilling, China yuan, Finland markka, France franc, Hong-Kong dollar от времени.
Значения
═между обменными
курсами Switzerland franc и Australia dollar, Austria schilling, China yuan, Finland markka, France franc, Hong-Kong dollar от времени.
Значения ![]() ═и
═и
![]() ═оценивались
в скользящем окне длиной 256 отсчетов, для подсчета использовался 401 отсчет с
01.01.90 по 15.07.91. Из рисунка 3 ═для меры близости
═оценивались
в скользящем окне длиной 256 отсчетов, для подсчета использовался 401 отсчет с
01.01.90 по 15.07.91. Из рисунка 3 ═для меры близости ![]() ═видно, что обменные
курсы образуют кластеры, которые зависят от времени. По всей видимости, это
основная причина, из-за которой в таблице 1 для последних 15-20 обменных курсов
соответствие между значениями мер близости
═видно, что обменные
курсы образуют кластеры, которые зависят от времени. По всей видимости, это
основная причина, из-за которой в таблице 1 для последних 15-20 обменных курсов
соответствие между значениями мер близости ![]() ,
, ![]() ═и номерами кластеров,
полученных с помощью алгоритма k-Means, не очень хорошее. Другая причина может заключаться в том, что
расстояния (
═и номерами кластеров,
полученных с помощью алгоритма k-Means, не очень хорошее. Другая причина может заключаться в том, что
расстояния (![]() и
и ![]() ), использовавшиеся в
алгоритме k-Means при разбиении
временных рядов на кластеры, чувствительны к наличию тренда. Для более
глубокого тестирования необходимо реализовать новый вариант алгоритма k-Means, где в качестве расстояния между рядами
использовались предложенные меры близости, и сравнить работу этого варианта
алгоритма со старым вариантом, когда использовались общепринятые расстояния
), использовавшиеся в
алгоритме k-Means при разбиении
временных рядов на кластеры, чувствительны к наличию тренда. Для более
глубокого тестирования необходимо реализовать новый вариант алгоритма k-Means, где в качестве расстояния между рядами
использовались предложенные меры близости, и сравнить работу этого варианта
алгоритма со старым вариантом, когда использовались общепринятые расстояния ![]() ═и
═и ![]() .
.
Заметим, что на основе рисунка 3 рассмотренные обменные
курсы валют все же можно приблизительно разделить на два кластера. Особенно это
хорошо видно из рисунка 4 для меры близости ![]() . В первый кластер входят Australia
dollar, Hong-kong dollar и China yuan (этот кластер можно условно назвать
европейским), во второй кластер входят Finland markka, France
franc и Austria schilling (это кластер можно
условно назвать восточноазиатским). Полученные наблюдения согласуются с
общепринятым разбиением рынка валютных операций на три географические зоны
активности [2].
. В первый кластер входят Australia
dollar, Hong-kong dollar и China yuan (этот кластер можно условно назвать
европейским), во второй кластер входят Finland markka, France
franc и Austria schilling (это кластер можно
условно назвать восточноазиатским). Полученные наблюдения согласуются с
общепринятым разбиением рынка валютных операций на три географические зоны
активности [2].
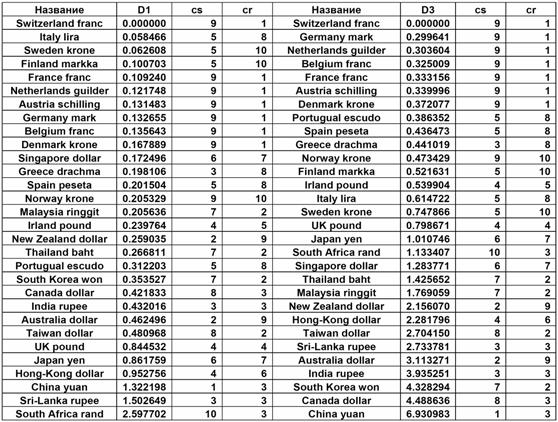
Табл.1. Значения мер близости ![]() ═и
═и ![]() ═вместе с результатами
кластерного анализа.
═вместе с результатами
кластерного анализа.
Предложенные меры близости также позволяют изучить,
насколько временные ряды близки на каком-то определенном масштабе. Для этого
можно вычислить меры близости, используя значения ![]() ═только для какого-то
определ╦нного масштаба
═только для какого-то
определ╦нного масштаба ![]() . Согласно перечисленным выше свойствам
вейвлет коэффициентов это будет равносильно сравнению спектров соответствующих
временных рядов в определенной полосе частот. На рисунках 5 и 6 показано, как
зависят меры близости
. Согласно перечисленным выше свойствам
вейвлет коэффициентов это будет равносильно сравнению спектров соответствующих
временных рядов в определенной полосе частот. На рисунках 5 и 6 показано, как
зависят меры близости ![]() ═и
═и ![]() ═между обменными курсами Switzerland
franc и Australia dollar, Austria schilling, China yuan, Finland markka,
France franc, Hong-Kong dollar от масштаба
═между обменными курсами Switzerland
franc и Australia dollar, Austria schilling, China yuan, Finland markka,
France franc, Hong-Kong dollar от масштаба ![]() . Для подсчета использовались 2048
отсчетов с 26.02.91 по 31.12.98. Из рисунков 5 и 6 видно, что для некоторых
обменных курсов мера близости принимает относительно малые значения для
небольших
. Для подсчета использовались 2048
отсчетов с 26.02.91 по 31.12.98. Из рисунков 5 и 6 видно, что для некоторых
обменных курсов мера близости принимает относительно малые значения для
небольших ![]() ═(на
коротких временных масштабах
═(на
коротких временных масштабах ![]() ), для других обменных курсов √ для
больших
), для других обменных курсов √ для
больших ![]() ═(на
длинных временных масштабах
═(на
длинных временных масштабах ![]() ). Рассмотренные обменные курсы опять
можно разделить на два кластера. В первый входят Australia dollar,
Hong-kong dollar и China yuan, а во второй √ Finland markka, France franc и Austria schilling. Также можно, применяя
скользящее окно (как это делалось выше), изучить, как изменяется мера близости
между временными рядами в определенной полосе частот в зависимости от времени.
). Рассмотренные обменные курсы опять
можно разделить на два кластера. В первый входят Australia dollar,
Hong-kong dollar и China yuan, а во второй √ Finland markka, France franc и Austria schilling. Также можно, применяя
скользящее окно (как это делалось выше), изучить, как изменяется мера близости
между временными рядами в определенной полосе частот в зависимости от времени.
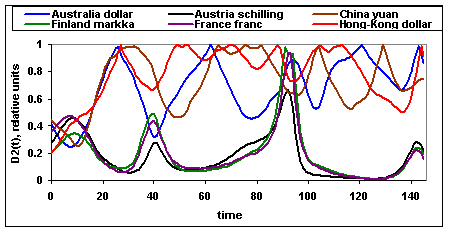
Рис.3. Зависимость меры близости ![]() ═от времени.
═от времени.
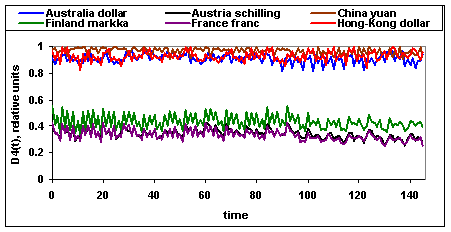
Рис.4. Зависимость меры близости ![]() ═от времени.
═от времени.
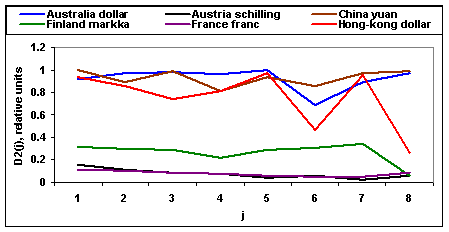
Рис.5. Зависимость меры близости ![]() ═от масштаба
═от масштаба ![]() .
.
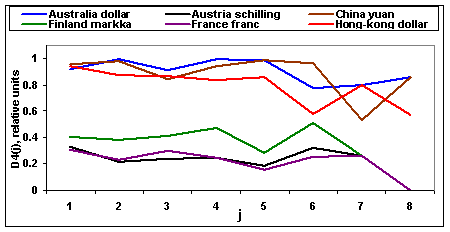
Рис.6. Зависимость меры близости ![]() ═от масштаба
═от масштаба ![]() .
.
Заключение
В работе предложена методика расчета мер близости между временными рядами на основе характеристик этих временных рядов, получаемых с помощью дискретного вейвлет преобразования. Подсчитанные по разработанному алгоритму характеристики ═1) робастны по отношению к изменению среднего ряда, тренду, масштабированию 2) независимы и нормально распределены. Эти свойства особенно необходимы, когда мера близости определяется между нестационарными временными рядами, поскольку обычное евклидово расстояние в качестве меры близости в таком случае не подходит. Подсчет вектора характеристик занимает линейное время, что очень важно при работе с большими объ╦мами данных. Эксперименты с финансовыми данными показали эффективность предложенных мер близости. В работе предложен метод оценки зависимости меры близости между временными рядами от времени. Разработанная методика также позволяет оценить меру близости между временными рядами на определенных участках спектра этих временных рядов.
Предложенную методику предлагается применять при
идентификации макроэкономических моделей для сравнения статистических и расчетных
временных рядов. В качестве вейвлет и масштабных фильтров рекомендуется
использовать фильтры Добеши с ![]() ═(см. приложение).
═(см. приложение).
Работа выполнена при поддержке РФФИ (код проекта 04-07-90346) и программы поддержки научных школ (код проекта НШ-1843.2003.1).
Литература
1. Бурнаев Е.В., Оленев Н.Н. Мера близости для временных рядов на основе вейвлет коэффициентов. Труды XLVIII научной конференции МФТИ. Часть VII. Москва √ Долгопрудный, стр.108-110, 2005.
2. Ширяев А.Н. Основы финансовой стохастической математики. Т.1. М.: Фазис, 2004.
3. Vidakovic B. Statistical modeling by wavelets, Wiley, 1999.
4. Kaufman L., Rousseeuw P.J. Finding Groups in Data: An Introduction to Cluster Analysis, Wiley, 1990.
5. Mallat M. A wavelet tour of signal processing. Academic Press, 2000.
6. Percival D.B., Walden A.T. Wavelet methods for time-series analysis. Cambridge university press, 2000.
Приложение: алгоритм дискретного вейвлет преобразования
Вейвлет и масштабный фильтры Добеши с ![]() ═равны
═равны ![]() ,
, ![]() ,
, ![]() ,
, ![]() ═и
═и ![]() ,
,![]() ,
, ![]() ,
, ![]() ═соответственно.
═соответственно.
Ниже приведен алгоритм, с помощью которого (это следует из
формул дискретного вейвлет преобразования из соответствующего раздела методики)
по масштабным коэффициентам ![]()
![]() ═можно подсчитать коэффициенты
═можно подсчитать коэффициенты ![]() ═и
═и ![]() ═
═![]() .
.
╥
![]()
o ![]()
o ![]()
o ![]()
o ![]()
╖
![]()
╖
![]()
╖
![]()
╖
![]()
o ![]()
╥
![]()
Используя
в качестве начальных данных ![]() ═
═![]() , с помощью алгоритма последовательно
получаем вейвлет
, с помощью алгоритма последовательно
получаем вейвлет ![]() ═
═![]() ═при
═при ![]() ═и масштабные
═и масштабные ![]() ═
═![]() ═коэффициенты.
Заметим, что подсчет этих коэффициентов с помощью данного алгоритма занимает
линейное время.
═коэффициенты.
Заметим, что подсчет этих коэффициентов с помощью данного алгоритма занимает
линейное время.