Мера близости для временных рядов на основе вейвлет коэффициентов
Е.В. Бурнаев, Н.Н. Оленев
Московский физико-технический институт (государственный университет)
Введение. Мера близости между данными является центральным понятием большинства data mining алгоритмов. Для ⌠сложных■ данных, таких как финансовые временные ряды, обычная мера близости типа евклидова расстояния, зачастую не применима. На рис.1. изображены обменные курсы South Africa rand и Switzerland franc по отношению к US dollar с 01.01.90 по 29.10.93, 1000 отсч╦тов. Очевидно, что подсчитанное для этих рядов евклидово расстояние значительно, хотя, если удалить тренд и провести подходящее масштабирование по оси ординат, окажется, что эти временные ряды близки.
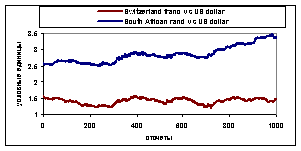
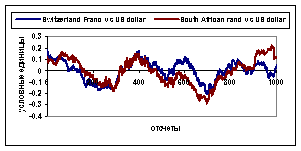
Рис.1. Слева: обменные курсы South Africa rand и Switzerland franc vs US dollar с 01.01.90 по 29.10.93, 1000 отсч╦тов. Справа: те же обменные курсы, но с вычетом тренда и подходящим масштабированием по оси ординат.
Из вышеприведенного примера ясно, что меру близости временного ряда следует рассчитывать на основе некоторых характеристик временного ряда, а не на основе значений ряда. Причем эти характеристики должны быть робастны по отношению к изменениям в уровне, масштабе и тренде ряда. В работе предлагаются меры близости для временных рядов на основе вейвлет коэффициентов, рассчитываемых с помощью дискретного вейвлет преобразования и обладающих этими свойствами.
Дискретное
вейвлет преобразование. Пусть ![]() ═- временной ряд,
═- временной ряд, ![]() ═для некоторого
целого
═для некоторого
целого ![]() ═и
═и
![]() .
Пусть
.
Пусть ![]() ═-
матрица дискретного вейвлет преобразования размера
═-
матрица дискретного вейвлет преобразования размера ![]() , определенная на основе вейвлет
и масштабного фильтров длины
, определенная на основе вейвлет
и масштабного фильтров длины ![]() ═[1]. Вектор вейвлет и масштабных
коэффициентов равен
═[1]. Вектор вейвлет и масштабных
коэффициентов равен ![]() , где
, где ![]() ═и
═и ![]() ═- вектора длины
═- вектора длины ![]() ═и
═и ![]() ═соответственно.
Пусть
═соответственно.
Пусть ![]() ,
тогда
,
тогда ![]() ═-
пропорционально среднему ряда, причем если в векторе
═-
пропорционально среднему ряда, причем если в векторе ![]() ═обнулить
═обнулить ![]() , а потом
сделать обратное вейвлет преобразование, то это равносильно вычитанию среднего
из ряда
, а потом
сделать обратное вейвлет преобразование, то это равносильно вычитанию среднего
из ряда ![]() .
Коэффициент
.
Коэффициент ![]() ═пропорционален
разности смежных взвешенных средних длины
═пропорционален
разности смежных взвешенных средних длины ![]() , то есть указывает на изменение
значений ряда на масштабе
, то есть указывает на изменение
значений ряда на масштабе ![]() . Модуль
. Модуль ![]() ═показывает, сколько энергии ряда
═показывает, сколько энергии ряда
![]() ═содержится
в отрезке частот
═содержится
в отрезке частот ![]() ═в момент времени
═в момент времени ![]() . Для широкого класса
стохастических процессов
. Для широкого класса
стохастических процессов ![]() ═независимы, и распределены как
═независимы, и распределены как ![]() , где
, где ![]() ═- некоторая
константа [1]. Коэффициент
═- некоторая
константа [1]. Коэффициент ![]() ═пропорционален взвешенному среднему длины
═пропорционален взвешенному среднему длины ![]() , а его модуль
показывает, сколько энергии ряда
, а его модуль
показывает, сколько энергии ряда ![]() ═содержится в отрезке частот
═содержится в отрезке частот ![]() ═в момент
времени
═в момент
времени ![]() .
В работе будут использоваться вейвлет и масштабные фильтры Добеши 4 (
.
В работе будут использоваться вейвлет и масштабные фильтры Добеши 4 (![]() ). В этом случае
). В этом случае
![]() ═не
чувствительны к линейному тренду, то есть если ряд
═не
чувствительны к линейному тренду, то есть если ряд ![]() ═суть значения некоторой линейной
функции, то
═суть значения некоторой линейной
функции, то ![]() .
При подсчете вектора коэффициентов
.
При подсчете вектора коэффициентов ![]() ═неявно делается предположение о
возможности циклического продолжения ряда
═неявно делается предположение о
возможности циклического продолжения ряда ![]() :
:![]() . Если это не так, то значения ⌠граничных■
вейвлет коэффициентов будут подсчитаны неверно. Для фильтров Добеши 4 это
коэффициенты
. Если это не так, то значения ⌠граничных■
вейвлет коэффициентов будут подсчитаны неверно. Для фильтров Добеши 4 это
коэффициенты ![]() ,
,
![]() ═и
═и ![]()
![]() .
.
Алгоритм подсчета мер близости между временными рядами.
- Пусть ряды
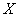 ═и
═и 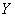 ═имеют
одинаковую длину. Подсчитываем вейвлет коэффициенты
═имеют
одинаковую длину. Подсчитываем вейвлет коэффициенты 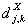 ═и
═и 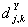 ═для
═для 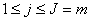 ═и
обнуляем ⌠граничные■ коэффициенты.
═и
обнуляем ⌠граничные■ коэффициенты. - Положим
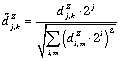 , где
, где 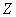 ═обозначает
либо
═обозначает
либо 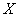 ,
либо
,
либо 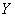 .
Вектора коэффициентов
.
Вектора коэффициентов 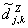 ═представляют характеристики ряда,
которые, как следует из вышеприведенных свойств вейвлет коэффициентов, 1)
робастны по отношению к изменению среднего ряда, тренду, масштабированию
2) независимы и нормально распределены. Длина такого вектора характеристик
равна
═представляют характеристики ряда,
которые, как следует из вышеприведенных свойств вейвлет коэффициентов, 1)
робастны по отношению к изменению среднего ряда, тренду, масштабированию
2) независимы и нормально распределены. Длина такого вектора характеристик
равна 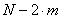 .
. - Пусть
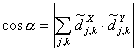 ═-
косинус угла между векторами характеристик. Положим
═-
косинус угла между векторами характеристик. Положим 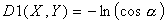 ═и
═и 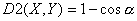 .
Поскольку коэффициент
.
Поскольку коэффициент 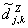 ═характеризует изменение в значениях
ряда
═характеризует изменение в значениях
ряда 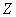 ═на
определенном масштабе в определенный момент времени, то для фильтра Добеши
4 имеет смысл определить меры близости на основе значения
═на
определенном масштабе в определенный момент времени, то для фильтра Добеши
4 имеет смысл определить меры близости на основе значения 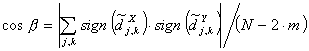 . Положим
. Положим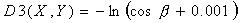 (добавка
(добавка
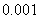 ═нужна
на тот случай, если первое слагаемое в аргументе логарифма равно нулю) и
═нужна
на тот случай, если первое слагаемое в аргументе логарифма равно нулю) и 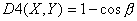 .
Преимущество
.
Преимущество 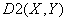 ═и
═и 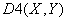 ═в том, что эти меры
близости ограничены. Качественной разницы между
═в том, что эти меры
близости ограничены. Качественной разницы между 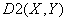 ,
, 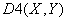 ═и
═и 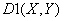 ,
, 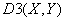 ═нет.
═нет.
Тестирование
мер близости. Для тестирования введенных мер
близости использовались ряды обменных курсов 30 валют по отношению к US dollar, взятые с сайта Federal Reserve Statistical Release, USA c 26.02.91 по 31.12.98, 2048 отсчетов (www.federalreserve.gov/releases/h10/hist/default1999.htm). В табл.1. приведены
значения мер близости ![]() ═и
═и ![]() ═между курсом Switzerland franc и остальными обменными курсами. Также в таблице приведены результаты
разбиения рядов на 10 кластеров с помощью алгоритма k-Means [2] (в столбцах указаны номера кластеров, к которым принадлежат ряды).
При разбиении на кластеры использовались два типа расстояния между рядами: cs
√ на основе косинуса угла и cr √ на основе
коэффициента корреляции между рядами. Из табл.1 видно, что между введенными
мерами близости и разбиением на кластеры, по крайней мере для первых 10 валют,
существует разумное соответствие. На рис.2. изображена зависимость мер близости
═между курсом Switzerland franc и остальными обменными курсами. Также в таблице приведены результаты
разбиения рядов на 10 кластеров с помощью алгоритма k-Means [2] (в столбцах указаны номера кластеров, к которым принадлежат ряды).
При разбиении на кластеры использовались два типа расстояния между рядами: cs
√ на основе косинуса угла и cr √ на основе
коэффициента корреляции между рядами. Из табл.1 видно, что между введенными
мерами близости и разбиением на кластеры, по крайней мере для первых 10 валют,
существует разумное соответствие. На рис.2. изображена зависимость мер близости
![]() ═и
═и ![]() ═между Switzerland
franc и Australia dollar, Austria schilling, China yuan, Finland markka,
France franc, Hong-Kong dollar
от времени. Значения
═между Switzerland
franc и Australia dollar, Austria schilling, China yuan, Finland markka,
France franc, Hong-Kong dollar
от времени. Значения ![]() ═и
═и ![]() ═оценивались в скользящем окне длиной 256
отсчетов, для подсчета использовались 401 отсчет с 01.01.90 по 15.07.91. Из
рис.2. видно, что курсы валют образуют кластеры, которые зависят от времени. По
всей видимости, это основная причина, из-за которой в табл.1. для последних
15-20 валют соответствие между значениями мер близости
═оценивались в скользящем окне длиной 256
отсчетов, для подсчета использовались 401 отсчет с 01.01.90 по 15.07.91. Из
рис.2. видно, что курсы валют образуют кластеры, которые зависят от времени. По
всей видимости, это основная причина, из-за которой в табл.1. для последних
15-20 валют соответствие между значениями мер близости ![]() ,
, ![]() ═и номерами кластеров,
полученных с помощью алгоритма K-means, не очень хорошее.
═и номерами кластеров,
полученных с помощью алгоритма K-means, не очень хорошее.
Работа поддержана грантом РФФИ ╧ 04-07-90346, программой НШ-1843.2003.01, целевой программой Президиума РАН ╚Информатизация╩.
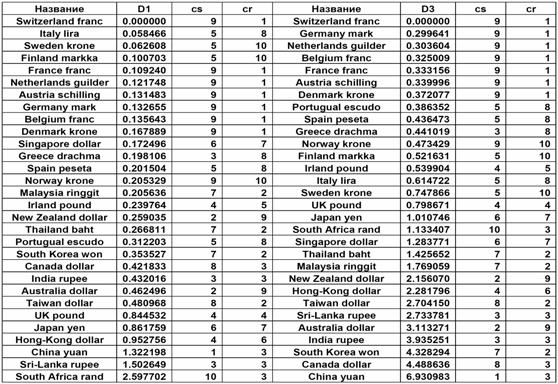
Табл.1.
Значения мер близости ![]() ═и
═и ![]() ═и результаты кластерного анализа.
═и результаты кластерного анализа.
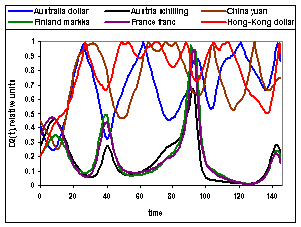
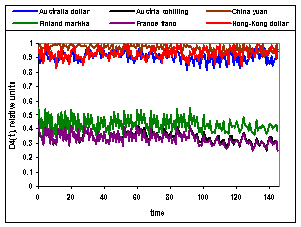
Рис.2.
Зависимость мер близости ![]() ═и
═и ![]() ═от времени.
═от времени.
Литература.
1. Vidakovic B. Statistical modeling by wavelets, Wiley, 1999.
2. Kaufman L., Rousseeuw P.J., Finding Groups in Data: An Introduction to Cluster Analysis, Wiley, 1990.