Let us start with an example. (Mathematical description is given in a paper published in 1994 in Russian and in a paper published in 1998 in English).
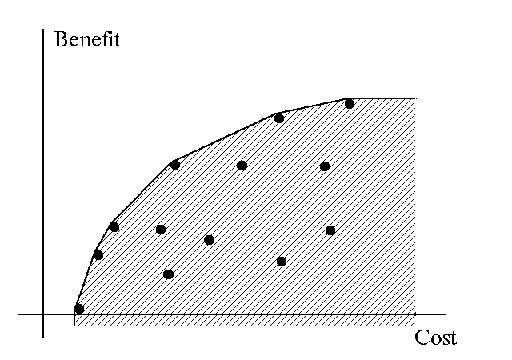
Let us suppose that only two attributes (cost and benefit) were chosen to be selection criteria. In the RGM, we display the convex hull of a finite number of criterion points, which is broadened by all dominated criterion points. This variety of points is called the Convex Edgeworth-Pareto Hull (CEPH). The CEPH is shaded in Figure.

User is provided with the CEPH, but not with the variant points. User may identify a most appropriate goal in the shaded space, but the identified goal only occasionally may be feasible - when it coincides with one of the points.
It is interesting to note that the efficient frontier of the CEPH coincides with the well-known cost-benefit curve. Cost-benefit analysis is often not sufficient for decision support, especially in public problems. Indeed, it is unable to consider several benefits (say, separate benefits of different population groups) and several costs. In addition, uncertainties or inaccuracies of estimates can not be incorporated directly into the cost-benefit analysis. So, multiple criteria development of the cost-benefit analysis is needed. This was done in the IDM/RGM technique.
Actually, the CEPH is treated as the variety of reasonable goals. User is informed about it and its efficiency frontiers with a help of the IDM technique. User has to express his/her preferences by identification of a reasonable goal. The information is used for selecting a small number of variants which are in line with the identified goal. In contrast to the FGM, several variants are selected instead of one decision in the convex case.
Selecting of several variants from the initial set on the basis of the reasonable goal is based on the following idea. The identified goal is considered to be a combination of aspiration levels. This means that we suppose that the user would prefer to achieve the identified levels of criterion values rather than to receive a criterion value which is better than the identified level. In the case of a finite number of feasible decisions, two options may occur:
i) there exist variants which are not worse than aspiration levels identified by user; and
ii) such variants do not exist.
In the first case, we loosely select those variants and display them to user. If such variants do not exist, we use the following idea: a modified point is related to any original feasible point. The meaning of aspiration level is used for constructing the modified points: if the original criterion value in a point is better than the aspiration level, the aspiration value is used instead of the original value. Then, usual Pareto domination is applied to modified points: non-dominated points are selected among them. Finally, the original feasible points which gave rise to selected modified points are displayed to user.
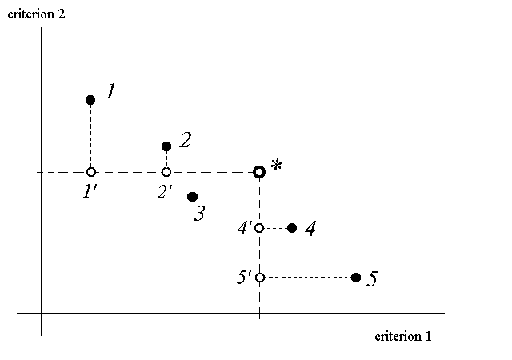
The Figure provides an illustration for the case of two criteria which are subject of maximization. The original feasible points are given by black circles, and the reasonable goal is denoted by a star. For any original point, a modified (white) circle is constructed (say, point 1-prime for point 1, etc.). The criterion value of a modified point equals to the minimal of two values: the criterion value of the original point and the aspiration level. If criterion values for an original point are less than the aspiration levels (like point 3), the modified point coincides with the original one. Pareto domination is applied to the modified points. Point 2-prime dominates (is better, than) point 1-prime, and point 4-prime dominates point 5-prime. So, three non-dominated modified points are left: 2-prime, 3, and 4-prime. For this reason, points 2, 3 and 4 correspond to the choice of the reasonable goal given by the star. They are displayed to user.
Note that other algorithms for selecting of preferred row can be applied.
The RGM technique proved to be effective for up to several thousands of decision variants. Normally, the number of selected elements is rather small and may be about twenty for several thousand of variants evaluated by, say, five criteria. Everything depends upon the geometry of point set. If the number of items is about several millions, the CEPH can be constructed as well, and so RGM technique may be applied, too. The RGM technique was coded in the form of VISUAL MARKET software systems. The demo version of the software system VISUAL MARKET/2 can be downloaded from the software section of our Web page.
One can be interested in the general RGM for non-linear mathematical models, which describe decision problems with infinite number of decision variants.