
MIKE11 and Interactive Decision Maps:
joint application in DSS for Water Quality Planning
Paper at the 3d DHI Software Conference
Danish Hydravlic Institute
Helsingor, Denmark, June 7-9, 1999
www.dhi.dk/softcon/papers/027/027.htm
A.Lotov, L.Bourmistrova, V.Bushenkov, R.Efremov,
Russian Academy of Sciences, Computing Center, Russia,
email:Lotov@ccas.ru http://www.ccas.ru/mmes/mmeda
A.Buber, N.Brainin,
Engineering and Research Center on Water Management,
Land Reclamation and Ecology “Soyuzvodpoekt”, Russia,
A.Maksimov,
Research Institute "Vodgeo", Russia
Abstract
A new approach to development of decision and negotiation support systems is described and applied in the DSS for water quality planning in large river basins. The approach is based on joint application of the well known system for modelling rivers and channels MIKE11 and of the new graphic tool for the search for smart strategies named Interactive Decision Maps / Feasible Goals Method (IDM/FGM). In addition to usual application of MIKE11 for simulation of given strategies, it is applied in the DSS as a data preparation tool for the IDM/FGM technique, which helps to select efficient strategies for further simulation. By this, new application field for MIKE11 is created. Moreover, combination of MIKE11 and IDM/FGM provides new dimensions in the search for smart water quality strategies.
The DSS based on combination of MIKE11 and IDM/FGM was calibrated on the basis of the hydrodynamic and advection-dispersion models of the Oka River and is used now in the framework of Russia’s federal programme “Revival of the Volga River”.
1. Introduction
The decision making process consists of two main steps:
The steps of decision making process are shown in Scheme 1.

Scheme 1. Steps of decision process
Modern simulation tools, which are usually combined with new information technologies like multimedia, virtual reality, and geographic information systems (GISs), provide to water managers new exciting opportunities of rapid graphic assessment of one or few water management strategies, i.e. they support the second stage of the decision making process. In contrast, they do not support a search for preferable strategies from large or infinite varieties of possible decision (screening of decision alternatives). Therefore, tools are needed, which are in line with the new information technologies and are able to support search for several decision strategies that will be studied in the stage of simulation analysis. Such tool is described in this paper. It is based on a graphic technique of Interactive Decision Maps / Feasible Goals Method (IDM/FGM). The technique displays information on the outcomes of an infinite variety of possible decision strategies in a graphic form and helps to select a small number of strategies, which are a subject of further detailed exploration in simulation analysis.
In water management problems, the IDM/FGM technique provides decision screening using simplified integrated models of water systems. In this paper water quality problem in a river basin is considered. So, a simplified integrated model of pollution transport in the river flow is needed. It constructed on the basis of simulation experiments with the system for modelling of rivers and channels MIKE11. To be precise, MIKE11 is used for parameterization of the advection-dispersion model of a river under consideration. Its application results in a simplified description of pollution transport in the form of influence matrix that is combined with a technological model of wastewater treatment. The integrated model obtained in this way is studied with the help of the IDM/FGM technique, which provides fast interactive graphic display of decision information in a form of decision maps (collections of efficiency frontiers of several pollution and cost criteria). This information helps user to identify a preferable feasible goal on a decision map with a click of computer mouse. An investment strategy resulting in the identified goal is computed automatically. Then, it may be checked and refined in simulation with MIKE11 and displayed in a GIS on the second step of the decision process. The investment strategy obtained in this way provides a starting point for development of a detailed project of water quality improvement in the river.
The problems of water pollution abatement in Russia’s rivers are of vital importance. Because of the complicated economic situation, the need for efficient application of environmental investments is very high. In order to get moderate investment, it is often necessarily to prove to federal and regional authorities, management and owners of enterprises, banks and other institutions, that the investment will result in a substantial improvement of environmental situation. These features made unsatisfactory the traditional technology of water quality planning, which was based on a single-criterion optimization. Therefore, a new technology and software for the search of cost-efficient strategies of environmental investment was developed and applied in the DSS, which is used now in the framework of Russia’s federal programme “Revival of the Volga River”. The technology was introduced in 1994 (Lotov, 1994; Lotov, 1998, Lotov, Bourmistrova and Bushenkov, 1999, Lotov, Bushenkov and Kamenev, 1999). It is based on the integrated assessment of decision problems with the help of the new graphic IDM/FGM technique. The DSS that incorporates the technology can be used by experts who prepare negotiator’s positions for the negotiation among officials of the Federal ministry for natural resources, regional authorities and other institutions involved in investment formation and allocation. Clones of the DSS may be used for the support of negotiation process.
This paper is devoted to decision and negotiation support of the first stage of decision making process. Section 2 of the paper discusses the usefulness of integrated models and describes application of MIKE11 for its constructing in the case of water quality management. Section 3 introduces the IDM/FGM technique and describes application of the technique for decision screening. In Section 4, the DSS is outlined and an example of decision screening in the framework of the DSS is provided.
2. Integrated models and their construction
Water management problems often have a very large (or infinite) number of alternative solutions. Nevertheless, most of computer-based DSSs provide an analysis for only a few decision alternatives. This means that the decision-maker has the complicated problem of selecting only a few alternatives for the simulation analysis. Experts usually are asked to solve the problem, i.e. to develop several decision alternatives so that decision-makers need not face the perhaps millions of options. The strategies experts suggest will reflect their experience, perceptions, and goals, which may well differ from those of the decision-makers. This can result in deadlock during the implementation phase, especially if decision-makers are forced to choose from among strategies which do not reflect their opinions or interests. Therefore a decision screening is needed that involves the decision maker.
The importance of decision screening in water management problems has been stressed by Dorfman (1965), who articulated the need for simplified models. Indeed one can not explore the whole lot of possible strategies on the basis of complicated detailed models. For this reason, simplified models must be used in screening procedures. Decision screening in environmental water management requires the integration of knowledge from a number of disciplines, which describe treatment of pollutants, pollutants transport, the effect of pollutants on the ecological systems, as well as the economic impacts, environmental measures, and so forth. Therefore, an integrated mathematical model must be constructed. It is supposed to combine simplified mathematical descriptions of the subsystems. Simplified models of the subsystems are needed because the original mathematical models that describes the subsystems in details are too complicated to be related directly one to another. In the case mathematical descriptions of the subsystems do not exist, expert judgments and empirical data may be used. The natural of a simplified model is an influence matrix.
2.1. Constructing of influence matrices
The most universal way to build an integrated model is to establish an approximation for the input-output dependencies, or parameterization, of the original model.
Let us start with a linear model. Consider a stationary linear model of partial derivatives describing the regional transport of a single pollutant from several pollution sources. Assume that the pollution discharge per unit time is constant and that the linear model can be used to evaluate the pollutant concentration at any point in the region. If formulated correctly, the problem of determining the concentration of the single pollutant is solved.
If pollutant discharge data are not known, the point source method can be used; source functions describing the concentrations that result from the individual source and the unit rate of discharge are constructed. Since the pollutant transport model is linear, the concentration at any given point (for example, at a monitoring station) may be calculated as the sum of the products of the source function values on real discharges. In other words, the concentration of the pollutant at this point is a linear function of pollution discharges, computed as the scalar product of the influence coefficient vector and the discharge vector.
Given the finite number of points where the pollutant concentrations are of interest, concentration values can be calculated by multiplying the influence matrix (its rows are provided by influence coefficient values) by the discharge vector. In the linear case, influence matrices can be calculated precisely by using the values of the source functions. In the nonlinear case, influence matrices can only approximate the dependencies of the pollution concentrations on the discharges; how they are constructed depends upon the particular scientific field. The universal approach is based on the application of regression analysis of data on input-output dependencies, obtained by the simulation of nonlinear models. Along with the approximation of an influence matrix, the simulation provides applicability ranges for its elements.
If it is impossible to construct a single influence matrix whose applicability range covers all possible inputs, several influence matrices may be developed. Each matrix is related to a certain applicability range; all of the matrices cover all possible inputs. Note that within the framework of environmental issues, an applicability range can describe a variety of input values that do not change the environmental system qualitatively. If the limits of this kind of applicability range are violated, it may not be possible for the system to exist in the same qualitative form.
If there is no adequate mathematical model for a subsystem, an influence matrix can be constructed through regression analysis of experimental or historical data. Sometimes, experts can provide both an influence matrix and its applicability range.
A combination of influence matrices and other simplified descriptions, balance equations, and restrictions imposed on variables contributes to an integrated model that describes an environmental system. Simplified integrated models are typically less precise then the original models; however, precision is not of paramount importance, as integrated models are used only to screen feasible strategies. Moreover, it is assumed that any strategy selected on a simplified model will be verified and improved later, through simulations with adequate models.
Now let us consider in details how coefficients of the influence matrix of water pollution were developed through simulation of detailed pollutant transport model using MIKE11.
2.2. Application of MIKE11 for constructing the influence matrix
Pollutant transport was described in the integrated model approximately by an influence matrix that made it possible to compute the concentrations of pollutants at the monitoring stations by multiplying the influence matrix by the discharge vector. In contrast to our previous DSS for water quality planning (Lotov, Bushenkov, Chernykh, 1997), the coefficients of the influence matrix were developed here through simulation with the pollutant transport model that is a part of MIKE11.
The influence matrix was calibrated for the Oka river, which is one of the largest inflows of the Volga river. The Oka river is 1,500 kilometer long, it has multiple inflows. Flow in the river is changing from 10 cubic meter per second during the summer dry period in the upper Oka till 1000 cubic meter per second in the lower Oka. Geometric characteristics, roughness and other parameters of the river-bed very variable.
In Figure 1, the map of the Oka river is provided. Seven regions which are located at the main flow of the river as well as several other regions are depicted. In accordance to the borders of seven main-flow regions, the river was split into fourteen segments. A monitoring station was located at the downstream end of each segment to monitor the concentrations of pollutants. The location of monitoring stations is provided in Figure 1, too.
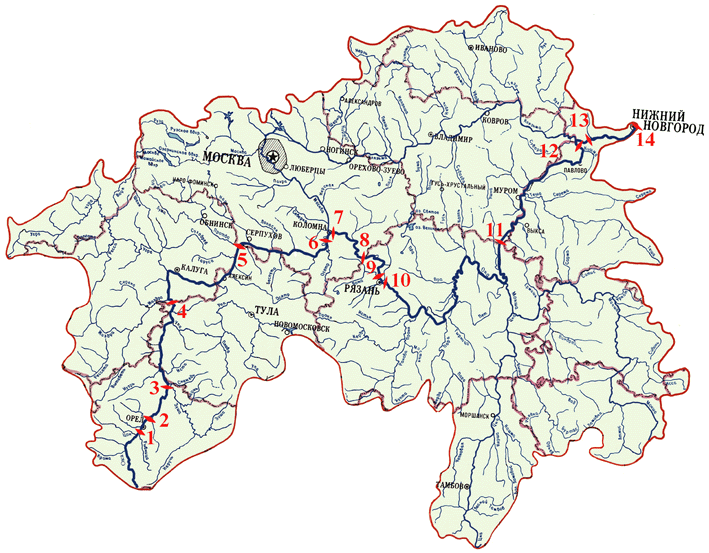
Figure1.
The hydrodynamic submodel of MIKE11 (HD MIKE11) was calibrated to the stationary flow of the Oka river with given water inflows during summer period with minimal flow. In the model, 23 main inflows were considered as well as 33 conditional inflows, which describe inflow from the neighboring land. The influence of the Volga river was taken into account in the model of the lower part of the Oka river. Calibration of the model was based on the data for the year 1982. It turned that the roughness coefficients used in the model were sufficient to describe the flow during the summer low-flow period. The map of depth and of river profile, which were obtained by modelling of the river, are provided in Figure 2.
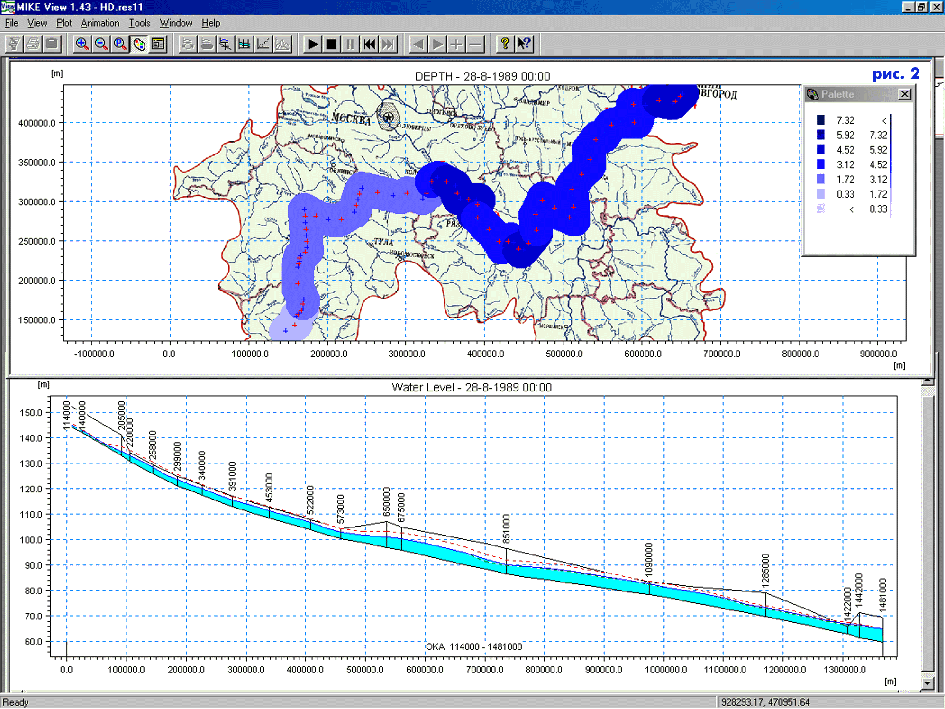
Figure 2.
The data on the hydrodynamics of the Oka river were used in the process of calibration of the advection-dispersion model of MIKE11 (AD MIKE11). AD MIKE11 was calibrated on the basis of information on concentrations of pollutants in the river and data on pollutants discharge into the river. The pollution of the river is determined by different sources, which include natural sources, industrial wastewater discharge, municipal wastewater discharge, urban non-point sources, agricultural non-point sources, large animal breeding enterprises.
Six pollutants were considered: BOD, suspension, phosphates, nitrates, oil products, and ferrous combinations. Data for pollutants concentration during summer low-flow period for several years for all inflows were analyzed. Average values were used in the process of modelling. The flow of the Oka river was split into several segments. Wastewater discharge data from large cities and for segments of the river were collected for the year 1989. The rest of the pollutants emission was spread among small rivers proportionally to their flow.
In the process of calibration of the model, the decay constants of the AD MIKE11 were adjusted. Sometimes data on emission were corrected, too. In Figure 3, one can see the concentration of nitrates in the water of the river computed by MIKE11 (data are artificial, but plausible). Red color is used at the points where the concentration is greater than one. Deep green is applied at the points where concentration of nitrates is close to the natural level.
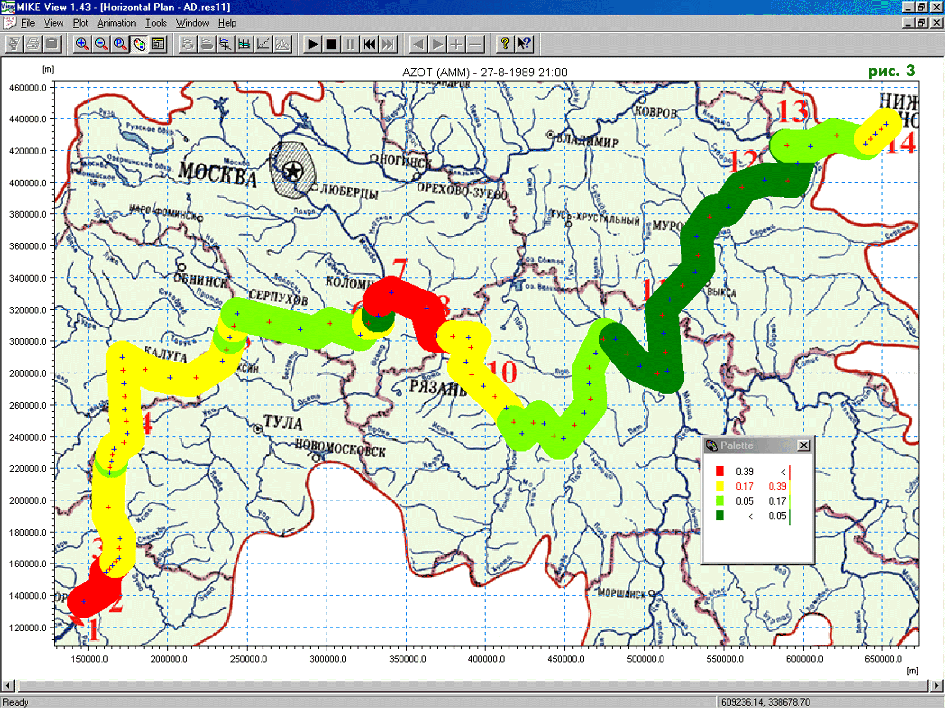
Figure 3.
Constructing of the influence matrix was based on the application of the calibrated submodel AD MIKE11. As it was said above, the river was split into fourteen segments. Monitoring stations were located at the downstream end of the segments. One or two regions were attributed to a segment: the left-bank region and the right-bank region. For some segments, the left-bank region and the right-bank region coincide. The emission of the regions in particular segments was evaluated. Wastewater emission of the regions in particular segments was evaluated. Sources of pollution were grouped into two groups: sources, for which discharge purification is possible (like industrial or municipal discharge), and sources, for which discharge purification is not possible (like non-point sources). Due to this, wastewater emission of regions was split into two parts: wastewater, which are a subject of treatment, and wastewater, which are not.
To construct the influence matrix, the following property of the advection-dispersion model MIKE11 was used: for a given water flow, the concentrations of the pollutants at the monitoring stations depend on the volume of pollutants emissions in a linear way in the model. This feature of the model, which can be proven theoretically or in an experiment with the model, can be used for constructing of the influence matrix in the following way.
It is clear, that in a river segment, three source of pollution emission do exist: emission from the region located at the left bank, emission from the region located at the right bank, and pollution, which is brought from the river segment located up to the river. In accordance to this fact, four simulation experiments were accomplished for any pollutant under consideration. In all experiments, pollutant flow at the monitoring station located at the downstream end of the segment was computed. In the first experiment, the pollutant flow at the upstream end of the segment, i.e. the pollutant flow at the downstream end of the upper segment, was set to the value given by MIKE11 for the current situation. At the same time, emission of the pollutant from the both regions located in the river segment under consideration were set to be equal to the background emission. In the second experiment, the pollutant flow at the upstream end of the segment was set to be the background flow. At the same time, emission of the pollutant from the left-bank region was set to be equal to the current emission, while emission from the right-bank region was set to be equal to the background emission. In the third experiment, the pollutant flow at the upstream end of the segment was set to be the background flow, emission of the pollutant from the left-bank region was set to be equal to the background emission, while emission from the right-bank region was set to be equal to the current emission. Finally, in the fourth experiment, all sources of the pollution were set equal to the current level. Results of the three first experiments were sufficient to estimate the coefficients of the linear model of the pollutant flow in the segment, in which pollutants flow at the monitoring point of the segment under consideration is a linear function of its flow from the upper segment and emissions from the both banks. These coefficient provide information for the influence matrix of the pollutant under consideration for the whole river. The fourth experiment was used as a control experiment. It turned that the pollutant flow computed in the fourth experiment was precisely the sum of the pollutant flows calculated in the first three experiments. By this the linearity of the influence of the pollution sources was confirmed. The influence matrix was used in the integrated model for the estimation of the influence of a decrement of a pollutant discharge on its flow at monitoring stations.
2.3. Description of the integrated water quality model
The structure of the simplified integrated model used in the DSS was chosen in accordance to the data on wastewater discharge prepared by the experts. Unfortunately, the collected data were very rough. For example, in contrast to the previous DSS for water quality planning based on the IDM/FGM technique (Lotov, Bushenkov, Chernykh, 1997), wastewater discharge was not attributed to particular industries or services, but to regions only. In the case of more detailed data, more detailed model could be used.
A stretch of river was divided into a number of segments, with a monitoring station at the downstream end of each segment to monitor the concentrations of industrial pollutants. The concentrations of pollutants were considered in summer, during the dry season.
The model of the river consists of two sub-models:
As it was described above, pollutant transport was described in the integrated model approximately by an influence matrix. Discharge treatment processes also were described in a simplified form. The wastewater discharge in a river was attributed to regions. The wastewater discharge treatment model, which relates the decrement pollution emission to the cost of the installation, was based on the concept of wastewater purification technology. A wastewater discharge treatment installation was supposed to be a combination of technologies. The database of the discharge treatment technologies was developed by the experts.
So, the decision variables of the model are the distributions of the regional wastewater among purification technologies. By identifying the decision variables, one could define the regional and total cost as well as the resulting concentration of pollutants in monitoring stations. Since we do not suppose decision makers to identify the decision variables in advance, we have to apply a different technique - the IDM/FGM technique. Application of the IDM/FGM technique starts with the choice of criteria which will be used for decision screening. To involve different decision makers with different interests, we provide a large list of performance indicators, among which the criteria may be selected.
The list of performance indicators includes two kinds of them:
One can choose from two to seven of performance indicators to be screening criteria in the framework of decision screening. As it was said above, strategy options are screened by a user by means of the IDM/FGM technique that support the exploration of efficient frontiers among aggregated economic and environmental choice criteria, and the identification of a feasible goal. Let us consider the IDM/FGM technique.
3. The FGM/IDM technique
Sometimes, the single-criterion optimization is considered to be adequate to help to screen the decision alternatives. For environmental problems, however, there is rarely a single criterion situation: decision screening must be based on multiple-criterion methods. Examples of their use in water management are described in Cohon and Marks (1975), Cohon (1978), Loucks, Stedinger, Haith (1981), Moiseev (1982), and Louie, Yeh, Hsu (1984). In this paper multiple criterion technique of IDM/FGM is applied. It was described earlier in a lot of papers and books, say (Lotov, 1984, 1989, 1994 and 1998, Lotov, Bushenkov, Chernov a.o., 1997, Lotov, Bushenkov, Chernykh, 1997, Lotov, Bushenkov, Kamenev, Chernykh, 1997). This section offers an informal introduction of the technique. Mathematical description of it is given, say, in (Lotov, 1996, Lotov, Bushenkov, Kamenev, 1999, and Lotov, Bourmistrova, Bushenkov, 1999). We introduce the technique on the basis of several examples.
4.1. Efficiency frontiers
Let us start with decision screening in the case of two criteria:
In Figure 4, the values for the pollution criterion are represented along the vertical axis, and values for the total cost are given along the horizontal axis. The feasible values of the two criteria are given by the colored area. All values outside the colored area are not feasible. One can see that the value of the cost F changes among zero and $2,876 million. The value of pollution Z5 changes among 0.83 and 3.4. Zero cost is related to the maximal value of pollution, i.e. Z5=3.4. Vice versa, the value of minimal pollution Z5=0.83 is related to the maximal cost F=$2.876 billion. It is clear one can not afford this cost. So, cost must be decreased, but, as the result, pollution will increase. What feasible point can provide a reasonable balance? To explore this question, we take into account that one is interested in the decrement of both criteria. Therefore, the frontier of the colored area in Figure 4 (so called efficiency frontier) is of interest. It displays the efficiency (criterion) tradeoff, i.e. it shows how much one has to pay for the decrement of pollution.
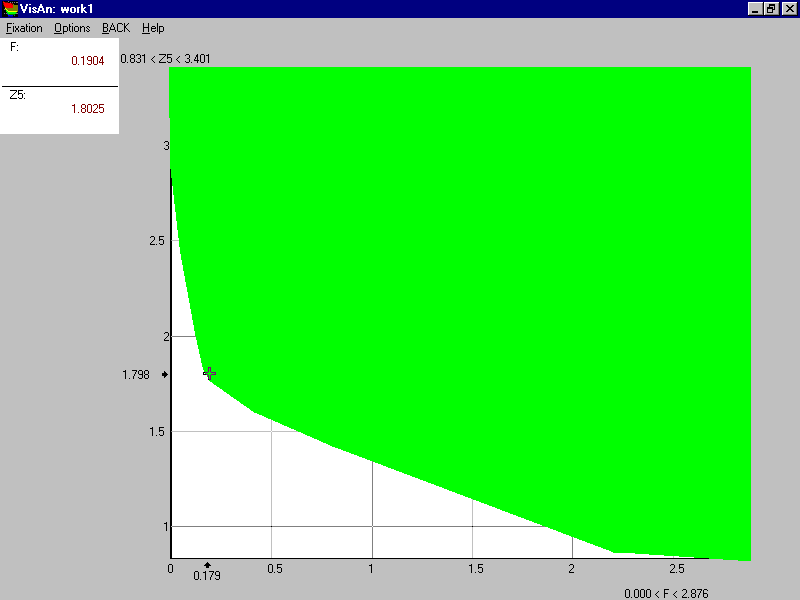
Figure 4.
One can see that the pollution can decrease substantially till Z5=1.78 while the cost is not greater than $190 million (this point on the efficiency frontier is given by the cross, and its precise values are given in the box in the upper left corner). So, about one half of the possible pollution decrement is provided only by 7% of the maximal investment! Further investment, however, isn’t so efficient: the slope of the frontier changes drastically in the vicinity of the cross. One can easily estimate that pollution about Z5=0.85 can be achieved for $2.2 billion, and the rest of investment (about $700 million) is practically inefficient!
As it was stressed above, the knowledge obtained from Figure 4 includes information about feasible criterion values as well as the information on how much one has to pay for the additional improvement of environmental criterion. The last type of the information is extremely important. It may be the decisive knowledge in the decision process. It is worth mentioning that the notion of efficiency tradeoff clearly differs from the notion of value tradeoff used by Keeney and Raiffa (1976); the latter implies subjective compensation of losses in one criterion by gains in the other.
It is important that decision makers and other people interested in problem receive the knowledge in a clear graphic form. Moreover, any of them can identify a preferable point on the efficiency frontier. Say, in Figure 4 the point of kink at F=$190 million and Z5=1.8 was identified. This point is actually the goal, but, in contrast to usual goal methods, it is feasible! This means that there exists an investment allocation strategy that results in the identified goal, i.e. total cost and pollution. The strategy will be computed automatically in about a minute. To start the computation of the strategy, one has loosely to double-click computer mouse on the preferred efficient point. This way this method is denoted by us the Feasible Goals Method (FGM).
The idea to apply pictures of the kind was proposed in the case of two criteria in by S.Gass and T.Saaty (1955) and transformed into a important direction of multiple criterion decision support (so called efficient set generation methods) by J.Cohon (1978). The IDM/FGM technique described here develops the idea of Gass, Saaty and Cohon for the case of multiple criteria (three, four, five, six, and may be more). The Interactive Decision Maps (IDM) is applied if the number of criteria is larger than two.
3.2. Interactive decision maps
Let us consider the IDM/FGM for the case of three criteria. We include the third criterion into account, namely the nitrates concentration (the maximal value in the for the whole river) denoted by Z4. Now the relation among cost and Z5 depends on the value of the third criterion Z4. Let us start exploration of the influence of Z4 with animation of the efficiency frontier among cost and Z5. In the framework of animation mode, a scroll-bar is provided under the picture with the efficiency frontier. The thumb of the scroll-bar displays the restriction imposed on the value of Z4 - the value of Z4 is not worse than the number given near the scroll-bar. If the thumb is close to its most right position, no restriction on Z4 is imposed, and so the efficiency frontier coincides with the frontier given in Figure 4. Automatic movement of the thumb from right to left results in the decrement of the value of Z4, i.e. the value of Z4 must improve. This results in the automatic movement of the frontier in the form of animation film (start ANIMATION 1).
It is important to stress that green colored areas in this case are slices of three-criterion variety of feasible criterion values. A particular slice displays the feasible values of Z5 and cost, for which the values of Z4 not worse than the value indicated by the thumb. Therefore, the efficiency frontier of green variety displays the criterion tradeoff among Z5 and cost if Z4 is not worse than the value indicated by the thumb.
Animation shows that the efficiency frontier starts to change substantially after Z4 is less than 2.5. Let us explore this effect in details. To do it, let us explore the snap-shots of the animation film. They are given in Figure 5. Once again, the values for Z5 are represented along the vertical axis, and values for the total cost are given along the horizontal axis. The value of Z4 is given in this picture by color. The relation among the value of Z4 and color is provided in the palette under the picture. One can see that the maximal value of Z4 is close to 5.5. So, red color corresponds to the pollution Z4=5.5, yellow color corresponds to Z4=4.5, light green color corresponds to Z4=3.5, blue corresponds to Z4=2.5, dark blue corresponds to Z4=2.0, pink corresponds to Z4=1.5. Note that slices related to different values of Z4 are overlapped. It is important that their efficiency frontiers do not intersect, they only touch sometime one another.
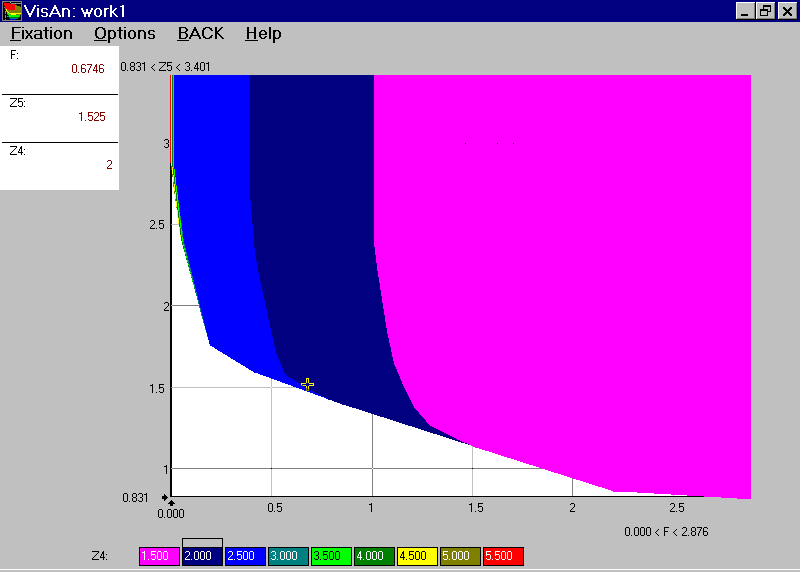
Figure 5.
One can see that all colors except deep blue and pink are seen in Figure 5 in a extremely narrow strip along the vertical axis. This evidence corresponds to the fact that the efficiency frontier in animation starts to change substantially after Z4 is less than 2.5. So, the problem related to high values of nitrates can be resolved with small cost (less than $20 million) in comparison with the problem related to oil products, which require hundreds of million. However, if concentration of nitrates must be less than 2.5, substantial money should be invested in addition. The quantity of the additional investment can be measured by the width of the deep blue strip. One can see that in the case of maximal oil products pollution (Z5=3.4) the additional cost for the decrement of Z4 from 2.5 to 2.0 is related to $400 million, and from 2.0 to 1.5 - to additional $600. However, if the value of Z5 is becoming not so high, the frontiers are getting closer, i.e. the additional cost related to the decrement of Z4 is getting smaller. For small values of Z5, the light blue strip and then the dark blue strip disappear, informing by this that the additional cost of the decrement of Z4 from 2.5 to 1.5 tends to zero. This information is given in a clear graphic way, too. Pictures of this kind are known as decision maps. A decision map thus plots the efficient frontiers between two criteria, for several restrictions imposed on the values of the third criterion. By this, a decision map provides a rough guide on the efficiency tradeoffs among three criteria.
To be precise, the FGM/IDM technique applies the concept of a modified decision map. In the standard decision map technique (Haimes et al., 1990), several cross-sections of the multiple-dimensional efficiency frontier of the feasible set in criterion space (FSCS) are depicted. Though the modified decision maps are similar to standard decision maps, they have several advantages. The most important of the advantages is their computing method.
Modified decision maps used in the framework of the IDM technique, are not prepared in advance. First an approximation of the Edgeworth-Pareto hull (EPH) of the FSCS is computed. The EPH is a set in the criterion space that, in addition to the feasible criterion values, also contains all dominated criterion values. The algorithm used to obtain the EPH is provided in short in (Lotov, 1996). For linear models, the EPH is a convex set in the criterion space. After the EPH is approximated, decision maps are obtained by computing and displaying efficient frontiers (cross-sections) of the EPH. Since the EPH in the criterion space is approximated in advance, several decision maps can be depicted in real-time. This why the name of the technique - Interactive Decision Maps. Later, references to decision maps will imply the modified version without any additional indication.
Decision maps have several features in common with topographical maps. Since the efficient frontiers of decision maps do not intersect (although they may sometimes coincide), they resemble the height contours of a topographical map. The value of the third criterion in a decision map is similar to height in a topographical map. Knowledge of topographical maps will aid in the analysis of decision maps. It is easy to view the variety of feasible combinations of the first and second criterion in relation to the value of the third ("places higher than..."). It is also easy to understand which values of the third criterion are feasible for a given combination of the first and second criterion ("height of this point is between..."). The proximity of efficient frontiers in the vicinity of a point indicates a slope, as in a topographical map: a slight shift in the efficient frontier results in a substantial change in the value of the third criterion.
In the three-criterion problems, the IDM technique may be used to provide arbitrary arrangement of criteria in decision maps. One can squeeze the criterion ranges. Moreover, one can change the number of tradeoff curves and zoom a map. Application of the IDM technique is much more important if four, five and more criteria are used. For example one can require any of the decision maps or any animation film. Moreover, animation or matrices of the decision maps may be displayed, too. This topic is considered in Section 4.
3.3. Feasible goals method
Once the exploration of a decision map is complete, the decision-maker may wish to identify a preferred feasible combination of the criterion values (a feasible goal). This is the main feature of the FGM. In 70s and the first part of 80s, feasible goals in the framework of the FGM technique were identified on the decision maps provided in special albums of decision maps printed out in advance (see Lotov, 1984). Now the IDM technique is applied, a preferred feasible goal can be identified on a decision map with a simple mouse click in the same way as in Figure 4. Let us squeeze the range of Z4 and explore the decision map while Z4 is between 2.6 and 1.2. Such decision map in provided in Figure 6.
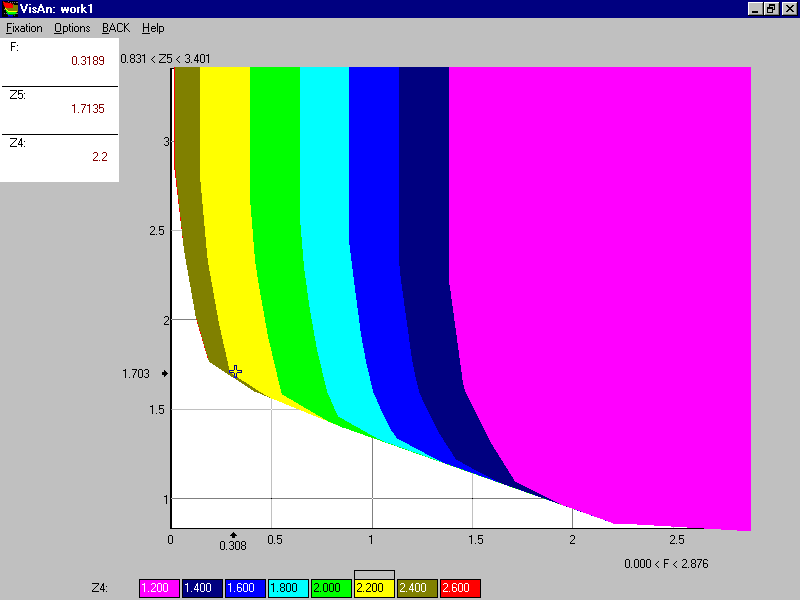
Figure 6.
One can see in Figure 6, that the additional cost related to the decrement of Z4 is relatively small if Z4 goes down from 2.6 to 2.2 while Z5 is about 1.7. Further decrement of Z4, however, requires a larger cost. More than $200 million are needed to decrease the value of Z4 from 2.2 to 2.0. Let us consider the cross given in Figure 6. Precise criterion values related to the cross are given in the box located in the left upper corner of Figure 6. They are F=$319 million, Z5=1.71 and Z4=2.2. The criterion combination given by the cross seems to be fairly reasonable. Let us suppose that this point was identified as a feasible goal. The wastewater treatment strategy that resulted in the identified values of cost and pollution criteria is computed automatically. The performance indicators related to the strategy are given in a table, upper part of which is provided in Figure 7.
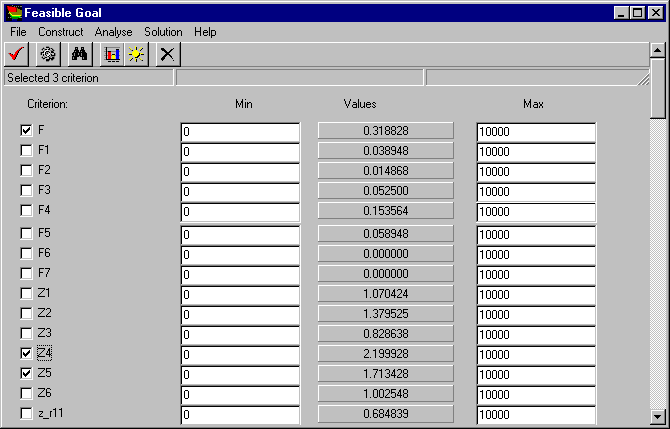
Figure 7.
The most left column of the table contains the list of performance indicators. One can “choose” indicators in small boxes located close to the indicator names. The indicators F, Z1, and Z5 were chosen for criteria studied in the above decision maps, and so they are clicked in the table. The other three column of the table contain the numbers. The left column displays the lower bounds imposed on the values of performance indicators, and the right column displays the upper bounds. Since the values of performance indicators considered in the model are between zero and ten, the restrictions given in the table are fulfilled automatically. Actually, no restrictions have been imposed in this particular case.
The central column contains the values of performance indicators that were computed in accordance to the goal identified in Figure 6. One can see that the value of the total cost of the project F and the maximal concentrations of nitrates (Z4) and oil (Z5) in the river are approximately the same as identified by the goal. To be precise, criterion values are a little bit better than the goal. The values of several other performance indicators are given in Figure 7, too. The indicators F1, F2,..., F7 display the investment allocation among seven regions located in the basin, and the indicators Z1, Z2,..., Z6 display the values of maximal concentrations of six pollutants in the river basin. Next indicators display the concentrations of pollutants in their regions. We do not consider them here.
4. Decision support system: an application example
The DSS includes the following subsystems:
The role of the subsystems is clear from their names. Only short comments are needed.
Information prepared in the first subsystem includes the influence matrix constructed with the help of MIKE11. Decision makers start their job with the second subsystem. They receive information on the current pollution in the river in a digital form, by usual diagrams as well as with the help of a GIS. After the criteria and restrictions are chosen (the table is used given in Figure 6), the EPH is computed. Exploration of the efficiency frontiers and identification of a feasible goal exemplified above is accomplished then. After it, a related strategy is computed and provided in a digital form, by diagrams and in the GIS.
Let us consider an example how the DSS can be applied for water quality planning. Though the data used in the example are not real, they are fairly plausible.
Figure 8 contains several diagrams of the second subsystem, which display pollution in the river without additional wastewater treatment. The upper (black) column diagram provides data on the river flow during dry summer season at all 14 monitoring points (cubic meters per second). Six other column diagrams display pollution (in relative units discussed above) at monitoring points. The left-hand column of diagrams contains data on (from the top) BOD, phosphorus and oil, while the right-hand column of diagrams contains data on suspension, nitrates and ferrous combinations.
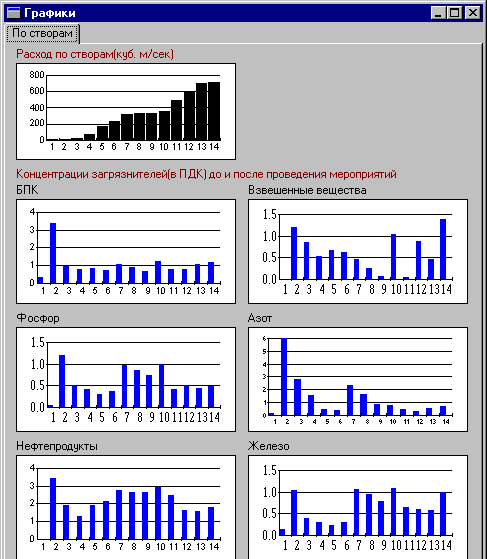
Figure 8.
One can see that among the pollution problems in the Oka river two most important problems may be articulated: pollution problems of the upper Oka river (monitoring stations 2 and 3) and pollution with oil products in all parts of the river. In this example, we consider the second problem. Let us suppose that the negotiations related to the investment into wastewater treatment facilities were started among representatives of the Moscow and Nizhny Novgorod regions that are economically most developed regions in the Oka river basin. Let us suppose that the following five criteria are used in the negotiations:
For the five criteria listed above the EPH was approximated, and now various decision maps can be studied. Figure 9 displays feasible concentrations of oil products at monitoring stations located in the Moscow region (horizontal axis) against feasible concentrations of oil products at monitoring stations located in the Nizhny Novgorod region (vertical axis). The upper scroll-bar informs that the total cost is restricted by $207 million. Restrictions imposed on the values of F4 and F7 are so high that they have no influence on the efficiency frontier.
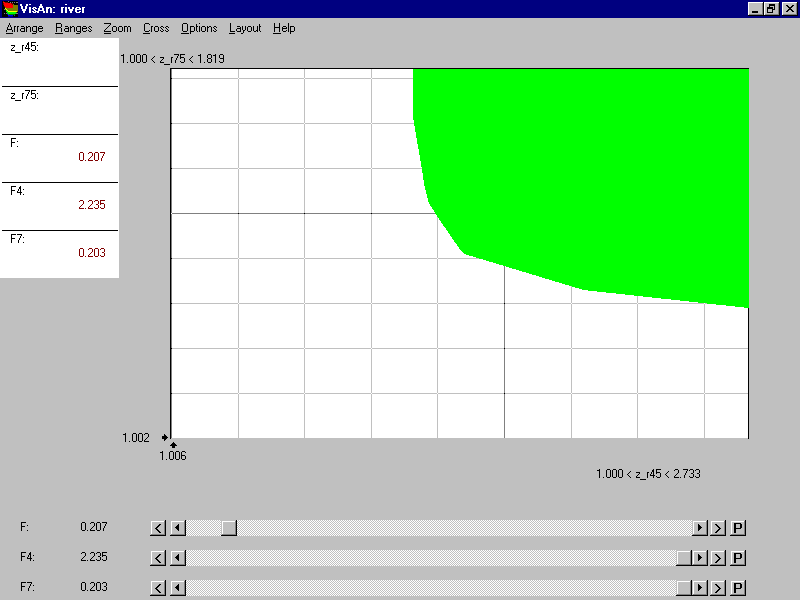
Figure 9.
One can see that oil pollution in the Moscow region and in the Nizhny Novgorod region are related if the total cost is restricted. Pollution in the Moscow region can decrease from the maximal (i.e. current) pollution F4=2.7 till the minimal pollution F4=1.75 that is minimal for this investment. If F4=1.75, the pollution in the Nizhny Novgorod region can not be less than F7=1.7. So, if $207 million are applied in the interests of the Moscow region, the pollution in the Nizhny Novgorod region can drop from the current F7=1.8 till F7=1.7, but not more. In contrast, if $207 million are applied in the interests of the Nizhny Novgorod region, the pollution in the Nizhny Novgorod region can drop until F7=1.3. The efficiency frontier among pollution in the Moscow and Nizhny Novgorod regions for the total cost of $207 million is clearly displayed in Figure 9.
Influence of the total cost on the efficiency frontier among the regional pollution under consideration is can be provided by an animation film, but this time we turn right a way to Figure 10, which contains the decision map.
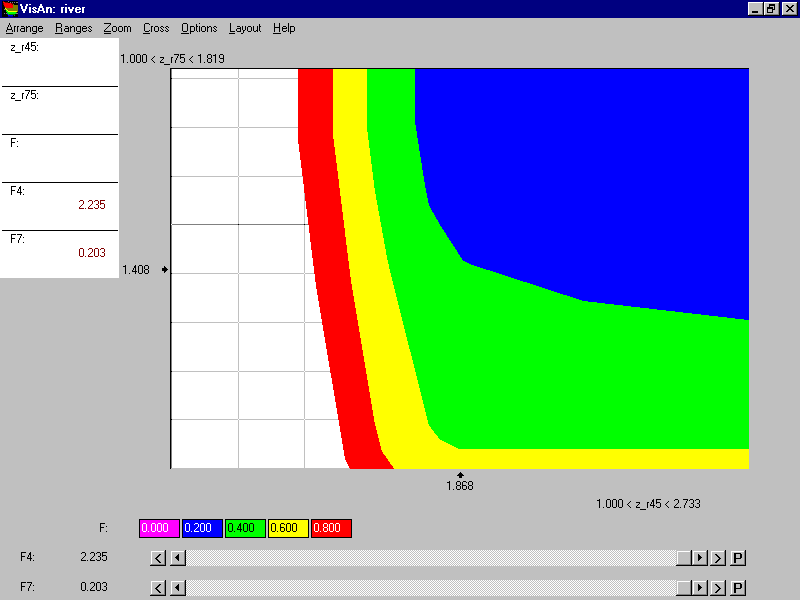
Figure 10.
The value of the total cost changes from zero till $800 with the step of $200 in the decision map. Once again, restrictions imposed on the values of F4 and F7 have no influence. It is clear that the form of the efficiency frontier substantially depends on the total cost. The cost of $200 solves the pollution problem to a large extent (compare the frontier of the blue curve with right upper corner which is related to zero cost). Additional $200 are very efficient, too (green slice). For example they can solve the problem for the Nizhny Novgorod region if the investment would be used according to the interests of that region. At the same time, minimal pollution in the Moscow region is achieved while F7 is about 1.7. Nevertheless, the representatives of the Nizhny Novgorod region can hope to make the representatives of the Moscow region to agree to move along the efficiency frontier from point F7=1.7 to the point of the kink (F7 less than 1.1) using minimal concessions in different topics. To understand the reason of it, let us look at the Figure 11.
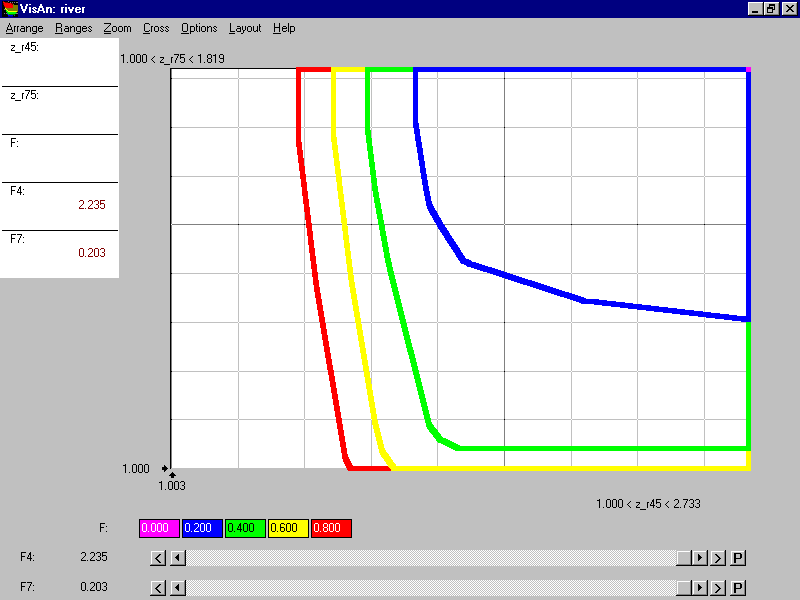
Figure 11.
Figure 11 contains the same decision map, which is given, however, in a different form: only efficient (weak-efficient, to be precise) frontiers of slices are displayed. The new form of the decision map provides more detailed information on the criterion values. One can easily understand that during the movement along the efficiency frontier (F=$400) from point F7=1.7 to the point of the kink (F7 between 1.1 and 1.2) the pollution level in the Moscow region increases from F4=1.6 to F4=1.8.
It is important that in this case further increment of the total cost is not related to the interests of the Nizhny Novgorod region since the Moscow region alone benefits from the additional investment. Figure 11 shows that the increment of the total cost from $400 to $600 results in the decrement of pollution in the Moscow region that is about 0.1 or 0.2 (depending on the pollution in the Nizhny Novgorod region). If the total cost would be increased from $600 to $800, F4 would decrease for 0.1 only.
Now let us consider the influence of the restrictions imposed on the investment in the regions. Two animation films are provided by us that display the influence. In ANIMATION 2, the decision map given in Figure 11 changes in accordance to automatic movement of the thumb of the upper scroll-bar while the thumb of the lower scroll-bar is in the most right position. (start ANIMATION 2)
In ANIMATION 3, the same decision map changes in accordance to automatic movement of the thumb of the lower scroll-bar while the thumb of the upper scroll-bar is in the most right position. To estimate influence of both thumbs at once, a matrix of decision maps can be used. (start ANIMATION 3)
In the matrix of decision maps given in Figure 12, the columns correspond to the values of F4, and the rows correspond to the values of F7. Related values are provided above the columns or to the right from the rows. The decision map displayed in Figure 11 is located now in the upper row of the most right column. It is related here to the restrictions on F4 (not greater than $800) and on F7 (not greater than $200), which do not influence the decision map still. By moving to the left (in the same row!) one obtains the snap-shots of the above animation film related to the influence of restriction imposed on F4. By moving downwards (in the same column!) one obtains the snap-shots of the above animation film related to the influence of restriction imposed on F7. Note that the number of columns and rows is restricted by the quality of the display only and may be regulated by user.
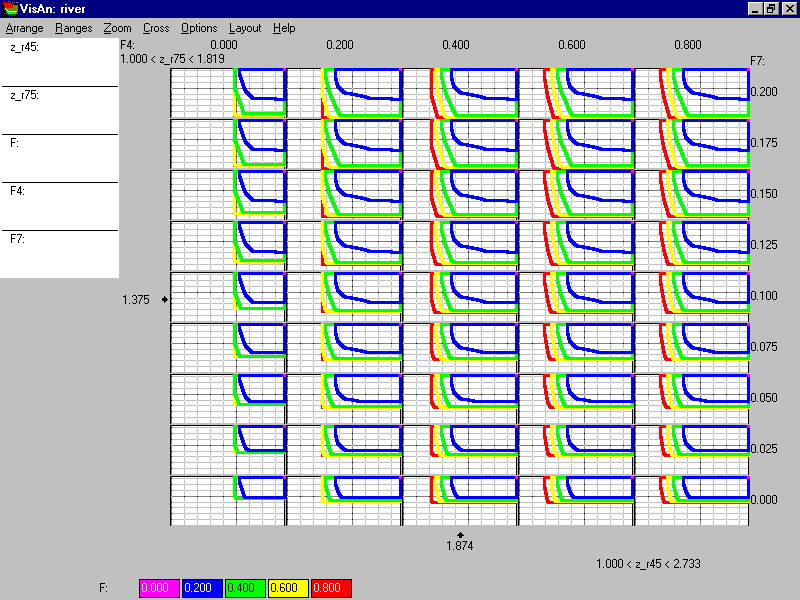
Figure 12.
Let us consider some features of the matrix of decision maps. For example, let us discuss the map located in the lower row of the most left column. The decision map is related to zero investment in both Moscow and Nizhny Novgorod regions (i.e. investment will be applied in other regions). It is interesting that in this case pollution in the Moscow region can fall until F4=2 and pollution in the Nizhny Novgorod region can fall until F7=1.5. Further improvement of water quality needs investment in these two regions! Total cost over $400 has no sense at all - red and yellow colors are not seen in the decision map.
Other decision maps show how relaxation of the restrictions on the investment in both regions influences the decision map. One can find multiple effects of such relaxation. For example, one explore changes in the efficiency frontier, which is related to the total cost of $200 million. Another effect is related to the role of the total cost of $800 million - red color is not seen in the most left column, i.e. $800 million can be efficiently invested only in the case the investment in the Moscow region is not too small.
Other matrices of decision maps can be easily displayed and explored. Double click of the computer mouse on a decision map results in the selection of the decision map for a detailed exploration. Let us suppose that a decision map was selected, which is related to the investment in the Moscow region not greater than $100 million and the investment in the Nizhny Novgorod region not greater than $20 million (Figure 13).
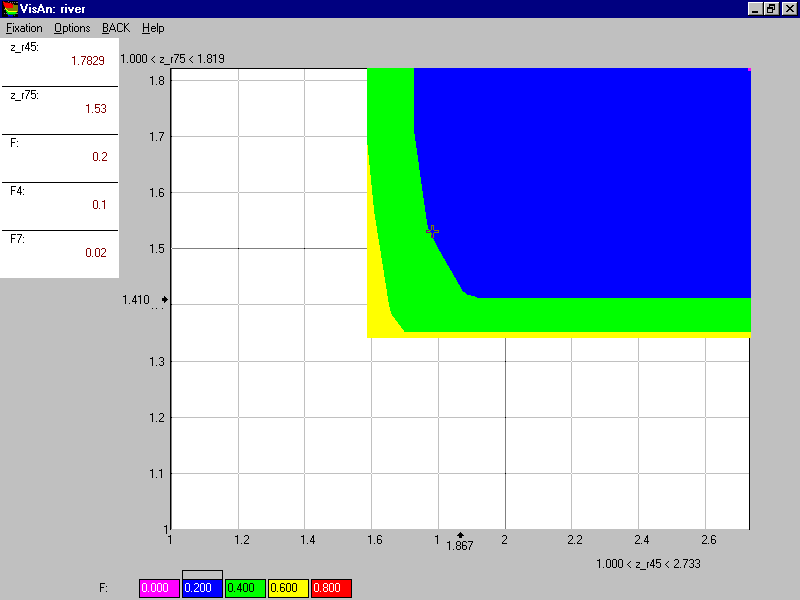
Figure 13.
One can see that red color is absent here - the total cost of $800 million has no sense. Moreover, it is clear that the total cost, which exceeds $200 million, isn’t too efficient. Suppose that the experts decided to explore more detailed decision map where the range of the total cost is among zero and $200 million. This decision map is given in Figure 14.
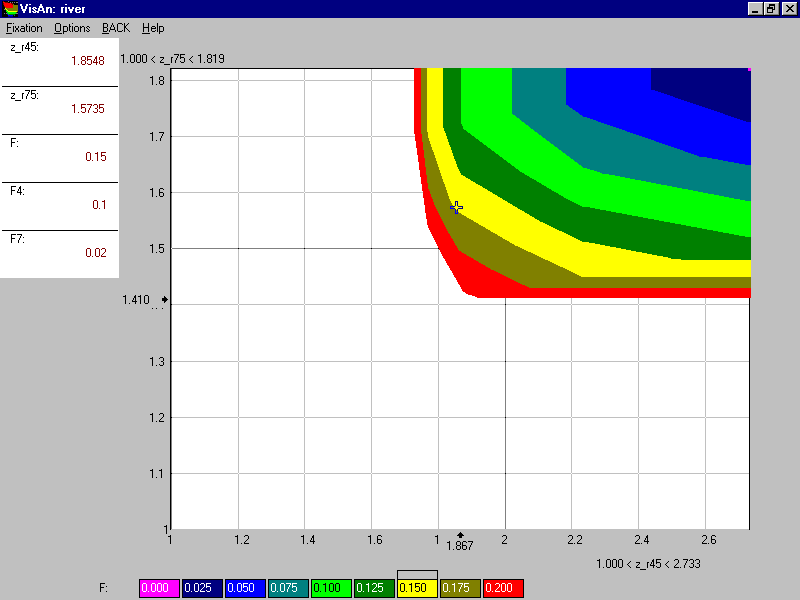
Figure 14.
The step of the total cost was selected in the decision map to be $25 million. One can see how the increment of cost influences the water quality. A feasible goal is identified in the decision map. It is related to the total cost of $150 million. The strategy, which results in the identified goal, is provided in Figures 15 and 16.
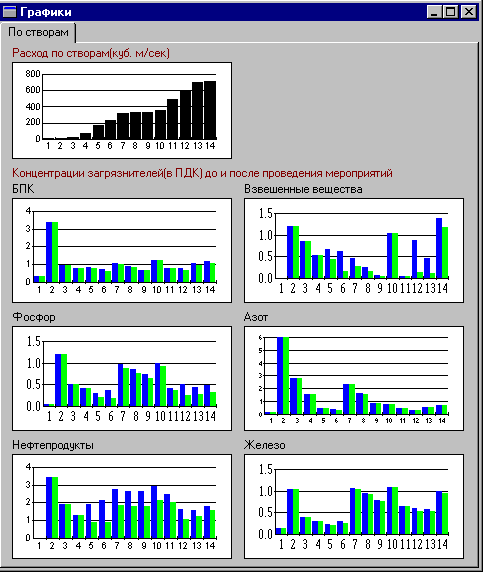
Figure 15.
Figure 15 is resembling Figure 8. In addition to current pollution concentrations, new pollution concentrations (i.e. pollution concentrations after the project will be completed) are displayed. One can see that oil products pollution has substantially improved in monitoring stations located lower than the Moscow region (monitoring stations 5,6, etc.). Nevertheless, it hasn’t been solved finally since investment is very low. Important that other pollution indicators improved as well.
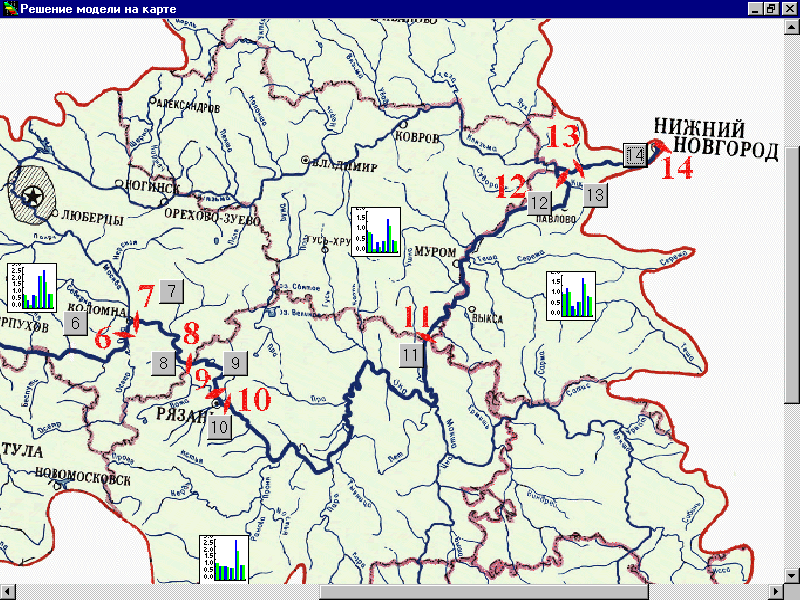
Figure 16.
In Figure 16, a GIS-generated map of a part of the Oka river basin is displayed. The display contains icons of two types that provide an opportunity to receive information about regional pollution levels, investments, pollutants discharge, etc. It is very interesting that $150 million of total cost were allocated in such a way that the investment in the Moscow region is $56 million and the investment in the Nizhny Novgorod region is $16 million. The rest is allocated among other regions where small volume of investent turned to be most efficent.
References
Cohon, J. (1978). Multiobjective Programming and Planning. New York: Academic Press.
Cohon, J. L. and D. M. Marks (1975). A Review and Evaluation of Multiobjective Programming Techniques, Water Resource Research 11(2).
Dorfman, R. (1965). Formal Models in the Design of Water Resource Systems, Water Resources Research 1(3).
Haimes, Y.V., K. Tarvainen, T. Shima, and J. Thadathil (1990). Hierarchical Multiobjective Analysis of Large-Scale Systems. New York: Hemisphere Publishing.
Lotov, A.V. (1984), Introduction into Mathematical Modeling of Economic Systems, Nauka, Moscow (in Russian).
Lotov, A.V. (1989) “Generalized Reachable Sets Method in Multiple Criteria Problems”, in: Methodology and Software for Interactive Decision Support. Lecture Notes in Economics and Mathematical Systems. v.337. Springer-Verlag.
Lotov, A. V. (1994). Integrated Assessment of Environmental Problems. Computing Center of Russian Academy of Sciences, Moscow, (in Russian).
Lotov, A. V. (1996). Comment to the Paper by D. J. White “A Characterization of the Feasible Set of Objective Function Vectors in Linear Multiple Objective Problems”, European Journal of Operational Research 89(1).
Lotov, A. (1998), "Computer-based support for planning and negotiation on environmental rehabilitation of water resource systems", in: D.P.Loucks (ed.) Rehabilitation of Degraded Rivers: Challenges, Issues and Experiences, Kluwer Academic Publishers, Dordrecht.
Lotov, A., Bourmistrova, L., and Bushenkov, V. (1999), "Efficient strategies. An application in water quality planning ", in: G. Kersten, Z. Mikolajuk, M. Rais, and A. Yeh (eds.) Decision Analysis and Support for Sustainable Development, Kluwer Academic Publishers, Dordrecht (in print).
Lotov, A.V., Bushenkov, V.A., Chernov, A.V., Gusev, D.V., and Kamenev, G.K. (1997), “Internet, GIS, and Interactive decision maps”, Journal of Geographical Information and Decision Analysis, v.1, No 2 http://www.geog.uwo.ca/gimda/journal2/
Lotov, A. V., V. A. Bushenkov, and O. L. Chernykh (1997). "Multi-criteria DSS for River Water Quality Planning", Microcomputers in Civil Engineering 12(1).
Lotov, A.V., Bushenkov, V.A., Kamenev, G.K., and Chernykh, O.L. (1997), Computer and Search for Balanced Tradeoff: Feasible Goals Method, Nauka, Moscow (in Russian).
Lotov, A. V., V. A. Bushenkov, and G. K. Kamenev (1999) Feasible Goals Method. Lewiston, NY USA: Edwin Mellen Press (in Russian).
Louie, P.W.F, Yeh, W.W.-G., and Hsu, N.-S. (1984), “Multiobjective water resources management planning”, Journal of Water Resources Planning and Management, 110(1).
Loucks, D.P., J.R. Stedinger, and D.A. Haith (1981). Water Resources Systems Planning and Analysis. Englewood Cliffs, NJ: Prentice-Hall.
Moiseev, N.N. (1982). Mathematical Problems of Systems Analysis. Moscow: Nauka Publishers (in Russian).