4.1. Постановка задачи линейного программирования.
Задачей линейного программирования (ЛП) называется задача минимизации или максимизации линейного функционала при линейных ограничениях. В литературе принят ряд специальных форм записи задачи ЛП:
- Форма общей задачи ЛП (задача ЛП со смешанными ограничениями) - найти максимум по переменным
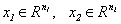 линейного функционала
линейного функционала
c1x1 + c2x2 → max
(0.10)
при линейных ограничениях
A11x1 + A12x2 ≤ b1,
(0.11)
A21x1 + A22x2 = b2,(0.12)
x1 ≥ 0.(0.13)
Здесь 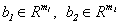 , матрицы A11, A12, A21, A22 имеют соответственно размеры
, матрицы A11, A12, A21, A22 имеют соответственно размеры
(m1 × n1), (m1 × n2), (m2 × n1), (m2 × n2).
- Стандартная форма записи задачи ЛП
(c, x) → max
при линейных ограничениях
Ax ≤ b
x ≥ 0.
Здесь 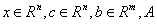 - матрица размера (m × n).
- матрица размера (m × n).
- Каноническая форма записи задачи ЛП
(c, x) → max
при линейных ограничениях
Ax = b
x ≥ 0.
Формально говоря, задачи 2-4 являются частными случаями общей задачи 1. Однако в свою очередь общая задача может быть представлена в форме любой из трех остальных. Так задача 1 принимает основную форму, если заменить в ней систему ограничений-равенств на эквивалентную систему ограничений-неравенств
A21x1 + A22x2 ≤ b2
-A21x1 - A22x2 ≤ -b2
Если сделать замену переменных
x2 = y2 - z2, y2 &ge 0, z2 ≥ 0,
то задача 1 примет стандартную форму. Если же ограничения неравенства в задаче 1 записать в виде
A11x1 + A12x2 + u = b1
где
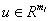
- дополнительная переменная(формально входящая в целевой функционал с нулевым коэффициентом) и вновь использовать замену переменных, то задача 1 будет иметь форму канонической задачи.
Вообще, любую задачу ЛП, на минимум или максимум, с неравенствами, направленными в ту или иную сторону, можно представить в любой из указанных форм. Для этого, наряду с приемами, перечисленными выше, необходимо использовать умножение целевой функции или ограничений-неравенств на (-1), что позволяет переходить от максимизации к минимизации и менять знаки неравенств.
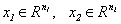 линейного функционала
линейного функционала
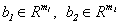 , матрицы A11, A12, A21, A22 имеют соответственно размеры
, матрицы A11, A12, A21, A22 имеют соответственно размеры 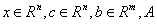 - матрица размера (m × n).
- матрица размера (m × n).