4.3.
Графический метод решения задачи линейного программирования.

Графический метод, несмотря на свою очевидность и применимость лишь в случае малой размерности задачи, позволяет понять качественные особенности задачи линейного программирования, характерные для любой размерности пространства переменных и лежащие в основе численных методов ее решения. Поясним графический метод на примере задачи ЛП в основной форме для n = 2

(c, x) → max

Ax ≤ b, где x = (x₁, x₂), c = (c₁, c₂), b = (b₁, b₂, ..., b_m), A - матрица размера (m × 2).

Очевидно, что при данной постановке задачи допустимое множество X в плоскости (x₁, x₂) представляет собой многоугольник (не обязательно замкнутый), образованный пересечением полуплоскостей H⁺_aibi (где a_i - i-я строка матрицы A, i = 1, ..., m), соответствующих ограничениям вида a_i1x₁ + a_i2x₂ ≤ b_i в исходной задаче. Линии уровня функции f(x) = (c, x) (линией уровня называется множество { }) образуют семейство параллельных прямых H_cα. При этом grad f(x) = c, т.е. градиент целевой функции всюду одинаков и является нормалью каждой из данных полуплоскостей. В соответствии с предыдущим, поиск решения задачи сводится к нахождению максимального числа α* среди всех таких α, что полуплоскость H_cα имеет непустое пересечение с X. При этом - множество решений задачи. При неограниченном решений может и не быть, т.е. при всех .

Из графического представления ясна характерная особенность задачи ЛП (при c ≠ 0): если ее решение существует, то оно достигается обязательно на границе. Отметим, что в рассмотренной задаче ЛП на максимум при поиске α* происходит как бы перемещение прямой H_cα в направлении вектора c. Если же решается задача ЛП на минимум, и, следовательно, ищется минимальное α*, удовлетворяющее указанным требованиям, то H_cα перемещается в направлении, противоположном вектору c.

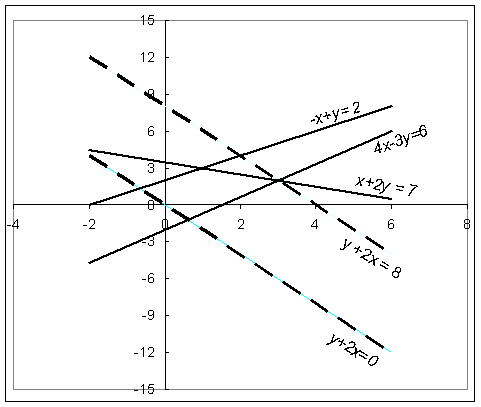
Пример 4.1. Пусть дана задача ЛП
2x + y → max
-x + y ≤ 2
x + 2y ≤ 7
4x - 3y ≤ 6
x ≥ 0, y ≥ 0/
Геометрическая интерпретация задачи приведена на рис. 1. Ясно, что решением является точка пересечения прямых
x + 2y = 7 и 4x - 3y = 6, т.е. (x*, y*) = (3, 2).

Рис. 1 Очевидно, что графический метод решения задач ЛП применим лишь в случае малой размерности пространства. В общем случае для решения задач линейного программирования в пространстве произвольной размерности широко используется симплекс-метод. Симплекс-метод решения задач ЛП основан на "разумном" переборе граничных точек допустимого множества. Подробное описание симплекс-метода решения задач ЛП можно найти, например, в [4,5].