Глава 2. Элементы теории неотрицательных матриц
Особенность матрицы A в модели В.В. Леонтьева состоит в том, что все элементы этой матрицы неотрицательны. Неотрицательные квадратные матрицы обладают рядом особых свойств. Изучению этих свойств посвящен специальный раздел теории матриц, основные сведения из которого приведены в данной главе. Изучение свойств неотрицательных матриц позволяет, в частности, дать ответ на поставленный в главе 1 вопрос: каковы условия существования неотрицательного решения 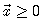 системы уравнений (0.2) при заданном
системы уравнений (0.2) при заданном 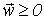 и A ≥ 0? Доказательство теорем, приведенных в данном разделе, можно найти, например, в [1, 2 ].
и A ≥ 0? Доказательство теорем, приведенных в данном разделе, можно найти, например, в [1, 2 ].
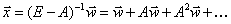 ,
,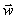 , нужно затратить вектор продуктов
, нужно затратить вектор продуктов 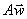 . Затем, чтобы произвести в системе набор продуктов
. Затем, чтобы произвести в системе набор продуктов 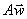 , придется дополнительно затратить
, придется дополнительно затратить 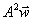 , и т.д. Сумма вектора конечного потребления и всех векторов промежуточных затрат
, и т.д. Сумма вектора конечного потребления и всех векторов промежуточных затрат 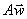 ,
, 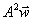 , ┘ и составляет вектор валового выпуска
, ┘ и составляет вектор валового выпуска 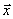 .
Соотношение (0.6) дает возможность вычислять итерационно объем валового выпуска
.
Соотношение (0.6) дает возможность вычислять итерационно объем валового выпуска 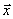 при известном объеме конечного выпуска
при известном объеме конечного выпуска 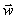 в модели (0.1) при условии продуктивности матрицы (E - A).
в модели (0.1) при условии продуктивности матрицы (E - A).
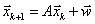 , где
, где 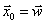 .
.
2.1. Критерии продуктивности неотрицательных матриц.
Определение 2.1. Матрица ![]() удовлетворяющая условию dij ≤ 0; при всех i ≠ j, называется продуктивной, если существует
удовлетворяющая условию dij ≤ 0; при всех i ≠ j, называется продуктивной, если существует ![]() такой, что
такой, что ![]() .
.
Определение 2.2. Матрица ![]() удовлетворяющая условию dij ≤ 0 при всех i ≠ j, называется прибыльной, если существует
удовлетворяющая условию dij ≤ 0 при всех i ≠ j, называется прибыльной, если существует ![]() такой что
такой что ![]() .
.
Замечание 2.1. Для модели (0.1) D = E - A.
Теорема 2.1. Пусть матрица ![]() удовлетворяет условию dij ≤ 0 при всех i ≠ j. Тогда следующие утверждения эквивалентны:
удовлетворяет условию dij ≤ 0 при всех i ≠ j. Тогда следующие утверждения эквивалентны:
- существует
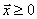 такой, что
такой, что 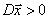 (продуктивность);
(продуктивность);
- для любого
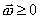 существует
существует 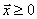 такой, что
такой, что 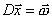 ;
; - последовательные главные миноры матрицы D положительны;
- все главные миноры матрицы D положительны;
- существует
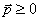 такой что
такой что 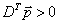 (прибыльность);
(прибыльность);
- для любого
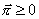 существует
существует 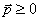 такой, что
такой, что 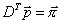 ;
;
- последовательные главные миноры матрицы DT положительные;
- все главные миноры матрицы DT положительны;
- матрица D неотрицательно обратима, т.е. существует D-1 ≥ 0.
Теорема 2.2. Пусть A - неотрицательная квадратная матрица. Тогда
- Если матрица (ρE - A) неотрицательно обратима, то ρ > 0 и ряд
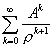 (0.5)сходится и его сумма равна (ρE - A)-1.
(0.5)сходится и его сумма равна (ρE - A)-1. - Если ряд (0.5) сходится и ρ > 0, то матрица (ρE - A) неотрицательно обратима.
(0.6)
Данный результат имеет очевидную экономическую интерпретацию. Для того, чтобы получить вектор конечного потребления (0.7)