МАГИСТРАЛЬ

Магистральная теория составляет важный раздел экономической теории, который разрабатывается математический аппарат для объяснения наблюдаемых в экономической статистике пропорций.

Вначале приведем образную интерпретацию, принадлежащую Дорфману, Самуэльсону и Солоу. Допустим, что некто хочет проехать по большому городу из пункта А в пункт Б. Если пункты А и Б расположены недалеко друг от друга, то скорее всего самый быстрый путь - это самый короткий. Однако если расстояние между А и Б велико, то самый быстрый путь оказывается чаще всего таким: надо из А выехать на одну из больших городских магистралей, где средняя скорость движения достаточно велика, не смущаясь тем, что мы, возможно, движемся в сторону от цели Б, по этой магистрали приблизиться, насколько возможно, к пункту Б и затем только с нее свернуть. Именно так возник научный термин "магистраль".

Будем измерять угловое расстояние между векторами в пространстве ═с помощью квазиметрики , положив для любых ═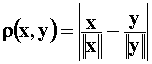. Квазиметрика обладает следующими очевидными свойствами:

╥ ═тогда и только тогда, когда векторы ═коллинеарны;

╥ для любых ═справедливо ;

╥ если , то .

Определение. Пусть ═траектория состояний экономической системы, полученная в результате решения некоторой экстремальной задачи из семейства задач, зависящих от временного горизонта . Скажем, что луч ═является магистралью для этого семейства задач, если для любого ═существуют такие числа ═и , независящие от , что выполняются условия ═для всех .

Если удается обосновать существование магистрали в имеющей экономическое содержание экстремальной задаче, то можно считать, что получено объяснение в каком смысле подержание пропорций экономического развития, определяемых вектором , является оптимальным.