ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ

Рассмотрим сначала систему уже существующих в какой-то момент времени предприятий. Согласно предположению 2 ее можно разбить на комплексы предприятий одного возраста. Такие возрастные группы часто называют когортами. Существенно учесть, что предприятия с возрастом портятся. Их мощность уменьшается, в то время как затраты ресурсов при работе на полную мощность могут даже возрасти по сравнению с исходным уровнем.

 

В результате технологическая база хозяйства в момент t представится картиной, условно изображенной на рис. 2.

По оси абсцисс отложен возраст предприятий t. Высота синих столбиков q_t(t) показывает производственную мощность, которой обладает в момент t когорта предприятий возраста t. Серый столбик показывает сколько текущих затрат Y_t(t) надо сделать, чтобы эти предприятия работали на полную мощность. Линия изображает среднюю материалоемкость когорты a_t(t)=q_t(t)/Y_t(t). Для самого левого столбика q_t(0)=Q_t, a_t(0)=n.

Предположим, что производственная система, с распределением мощности по ресурсоемкости, изображенном на рис. 2 может использовать не более, чем Y единиц сырья за год. Как распределить его между предприятиями, чтобы получить наибольший объем производства? Очевидно, что надо сначала надо полностью обеспечить сырьем предприятия с наименьшей ресурсоемкостью, т.е. те, которые образуют первый столбик на═ рис. 2. Обеспечив эти предприятия сырьем полностью, следует выделить сырье следующему столбику, и т.д., пока хватит сырья. Поэтому максимальный объем производства Y при затратах сырья Y выражается как

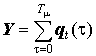══════════════════════════════ ══════════════════════════════════════════════════════════════════════════════════ (2)

где T_μ √ максимальный возраст, при котором еще выполняется неравенство.

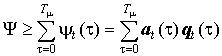═══════════════════════════════════ ══════════════════════════════════════════════════════════════════════════════════ (3)  ═══════════

На рис 2 T_μ √ это номер последнего заштрихованного столбика.

Когда затраты Y меняются, максимальный выпуск (2) тоже меняется. Зависимость , изображенная на рис. 3 вишневой линией, называется производственной функцией. Она характеризует максимальные производственные возможности хозяйства. Каким бы ни было распределение мощностей, эта функция будет монотонной и вогнутой, а ее график будет начинаться в точке (0,0). Вогнутость производственной функции математически выражает известный экономический закон убывающей производительности факторов производства. Таким образом, в предположениях 1, 2 возрастная структура мощностей определяет производственную функцию хозяйства.

═