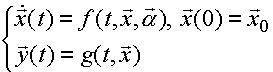Основным содержанием науки, по-видимому, можно признать формирование моделей того или иного типа на основе результатов наблюдений и исследования их свойств. Модели могут быть в разной степени формализованными, но все они обладают тем главным свойством, что связывают наблюдения в некоторую общую картину. Решение задачи построения математических моделей динамических систем по данным наблюдений за их поведением составляет предмет теории идентификации, которая тем самым становится элементом общей научной методологии.

Динамическая система, говоря нестрого, - это объект, в котором происходит взаимодействие между его разнотипными частями и формируются наблюдаемые сигналы.

Интересующие нас наблюдаемые сигналы обычно принято называть выходными сигналами. Все остальные сигналы называют возмущениями, причем возмущения могут быть разбиты на классы: входные сигналы, измеряемые и не измеряемые шумы.

Имея дело с системой, мы нуждаемся в некоторой схеме соотнесения между собой характеризующих систему переменных. Будем называть совокупность предполагаемых связей между наблюдаемыми сигналами моделью в широком смысле. Очевидно, что модели могут принимать самую разную форму и записываться с разной степенью математической детализации или вообще без использования языка математики. Однако в большинстве случаев соотношения, описывающие взаимодействие различных составляющих динамической системы, задаются в виде систем алгебраических, дифференциальных (разностных), алгебро-дифференциальных или интегральных уравнений. Такие модели принято называть математическими моделями (ММ). Математические модели могут быть снабжены рядом поясняющих прилагательных (непрерывные и дискретные по времени, сосредоточенные и распределенные, детерминированные или стохастические, линейные или нелинейные и т.п.) в зависимости от типа используемых уравнений.

При моделировании динамических систем все численные характеристики изучаемого процесса можно разбить на два класса: не изменяющиеся в ходе процесса (константы) и, соответственно, меняющие свое значение (переменные). В свою очередь, в каждом из этих классов можно выделить два подкласса: численные характеристики, которые могут быть измерены лабораторными методами в ходе эксперимента (измеряемые константы и переменные), и характеристики, которые либо вообще не могут быть измерены на современном уровне развития науки, либо их измерение чрезвычайно трудоемко и дорого (не измеряемые константы и переменные).

На первом этапе построения математической модели (ММ) любого процесса необходимо выбрать общую структуру модели и класс уравнений, которыми предполагается описать наблюдаемый процесс, т.е. решить так называемую задачу структурной идентификации. Что касается выбора структуры модели, то ее сложность определяется конечными целями исследования, теоретическими соображениями о механизме процессов и, не в последнюю очередь, возможностями измерений в ходе эксперимента и возможностями математического обеспечения обработки результатов.

Когда структура модели и класс уравнений определены, то необходимо определить числовые значения констант, вошедших в уравнения ММ.

На этом этапе построения ММ возникает задача нахождения числовых значений не измеряемых констант по имеющимся экспериментальным данным, т.е. по значениям измеряемых переменных (откликам). Данная задача называется задачей параметрической идентификации.

Целью решения задачи параметрической идентификации является подбор таких численных значений неизвестных констант модели, при которых решение задачи соответствовало бы, в некотором смысле, экспериментальным данным, причем найденные значения констант не должны противоречить физическому смыслу и теоретическим соображениям.

 

Общая постановка задачи параметрической идентификации

Пусть математическая модель процесса представлена в виде

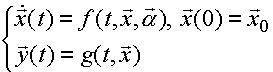, (В.1)

где t - независимая переменная (время),

- внутренние переменные модели,

- вектор параметров (констант) модели,

- вектор наблюдений (откликов) модели,

- некоторые функции.

Необходимость введения вектора наблюдений связана с тем, что, как правило, математическая модель процесса строится в терминах, не всегда поддающихся прямому измерению. Функция выражает переменные, поддающиеся измерению (отклики), через переменные, участвующие в построении модели. Другими словами, в терминах переменных и функции описывается модель исследуемого процесса, а в терминах переменных и функции описывается модель измерений. Причем надо отметить, что функция необязательно задает взаимно однозначное соответствие между внутренними переменными и откликами .

Далее, пусть в течении периода времени проводились экспериментальные наблюдения за поведением исследуемого процесса и в ходе эксперимента были получены значения откликов в некоторые моменты времени , т.е. была составлена матрица наблюдений

,

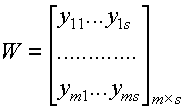
где , .

Задачу параметрической идентификации математической модели (1.1) по экспериментальным данным можно определить как задачу отыскания таких числовых значений параметров , при которых расчетные значения откликов модели наилучшим образом согласовались бы с экспериментально полученными.

Систему уравнений (В.1) можно переписать в операторной форме. Получим

, (В.2)

где оператор является суперпозицией функций , и оператора интегрирования задачи Коши системы (1.1),

.

Обычно вместо точного значения вектора откликовиз эксперимента известно лишь некоторое его приближение и, следовательно, вместо задачи (В.2) требуется решить задачу

. (В.3)

При этом решение задачи (1.3) не может быть в общем случае получено как , так как такого решения в классическом смысле может и не существовать для .

Как известно, задача решения операторного уравнения (1.2) является корректно поставленной по Адамару, если

Если же нарушается хотя бы одно из перечисленных требований, то задача называется некорректно поставленной.

Задача (В.3) является, в общем случае, некорректно поставленной задачей, так как вектор откликов может не принадлежать множеству (нарушение условия разрешимости), решение может быть неединственным или же обратный оператор может не обладать свойством непрерывности, и, следовательно, в этом случае решение не будет обладать устойчивостью к ошибкам.

Так как точное решение задачи (В.3) невозможно, ставится задача о нахождении приближенного в некотором смысле решения , которое чаще всего определяют из условия

, (В.4)

где - метрика пространства сравнения с .

Переход от задачи (В.3) к ее экстремальной постановке (В.4), конечно, не делает задачу корректной. Однако аппарат решения некорректных экстремальных задач типа (В.4) на сегодняшний день хорошо развит.

Первая страничка