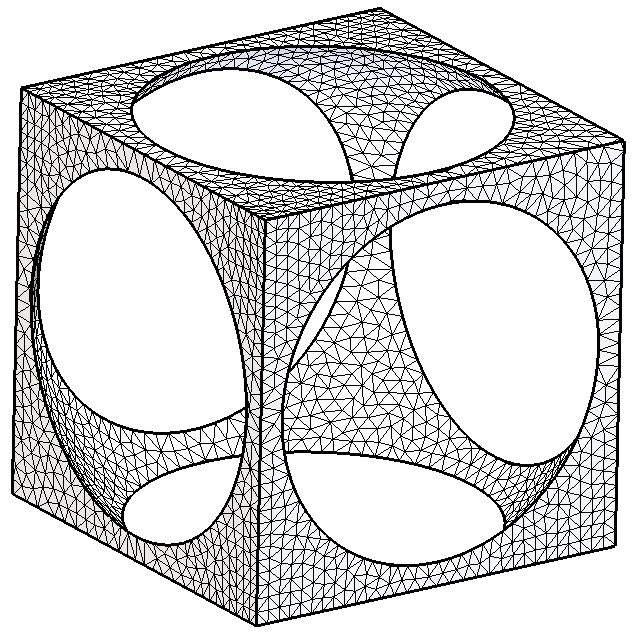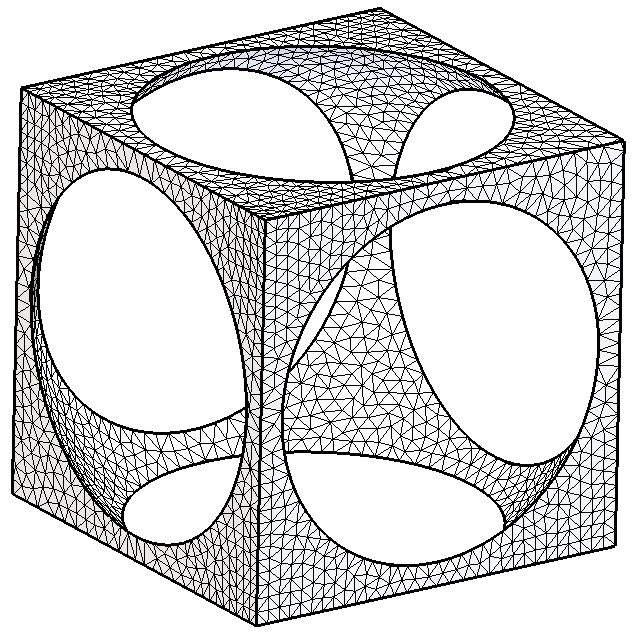group homepage                                                                                                          Russian version


sotm project: Delaunay mesh generator in implicit domains with Delaunay edge sharpening.

The idea of the algorithm goes back to the work by  Persson and Streng, 2004, who suggested to consider triangle or tet mesh as elastic network where each Delaunay edge is the elastic strut which resist compression but does not resists dilation. As a result of vertex repulsion and Delaunay edge reconnection 3d mesh expands and fills the implicit domain very similar to construction foam. In original paper by Persson and Streng mesh generator is just one page of the Matlab code. In 2008 in the paper by Belousova (Kudryavtseva) and Garanzha it was suggested to control this elastic network via special sharpening force which was suggested for visualization of implicit surface by A. Belyaev in 2002. Using this ideas, A.I. Belokrys-Fedotov developed C++ code which simultaneously recovers the shape of domain, constructs surface mesh with sharp edges and builds 3d Delaunay mesh without slivers.
The current version of the algorithm is the research one. It is much less efficient compared to well known tet meshing algorithms, say implemented in CGAL. However, to our knowledge, its unique feature is the possibility to construct 3d Delaunay meshes directly using analytically defined implicit domains with sharp edge recovery without prior prescription of sharp boundary edges.

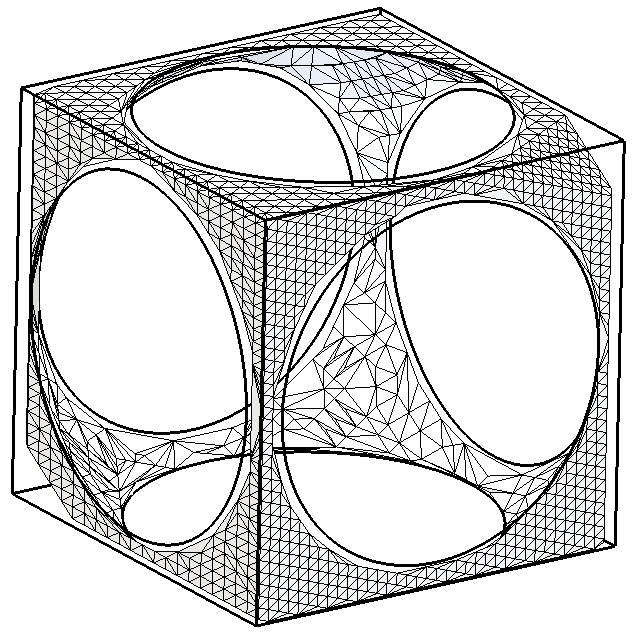
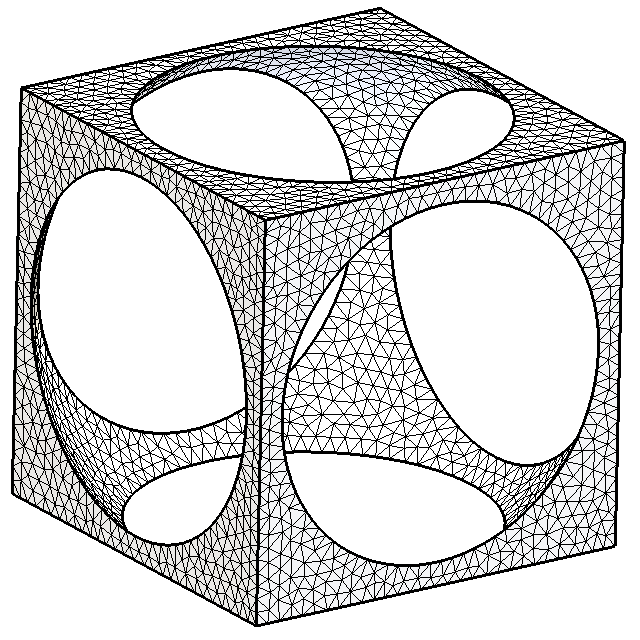
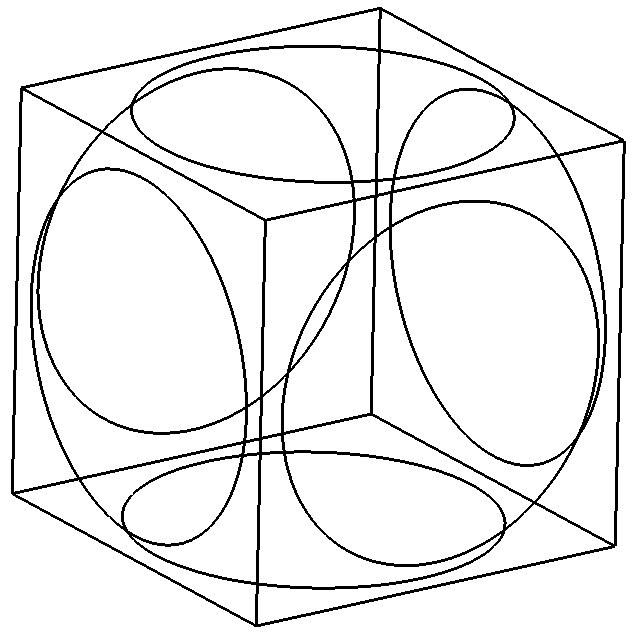
Algorithm behaviour is illustrated using test case from the paper by A.Belayev with co-authors, 2002. Initial mesh is shown which does not fill the domain. Intermediate stage with a few unrecovered edge fragment is shown. Next figure is fully recovered domain boundary but 3d tet mesh contain slivers. The last figure shows that sliver elimination does not destroy sharp boundary edges. Note that output is precisely the  Delaunay mesh.



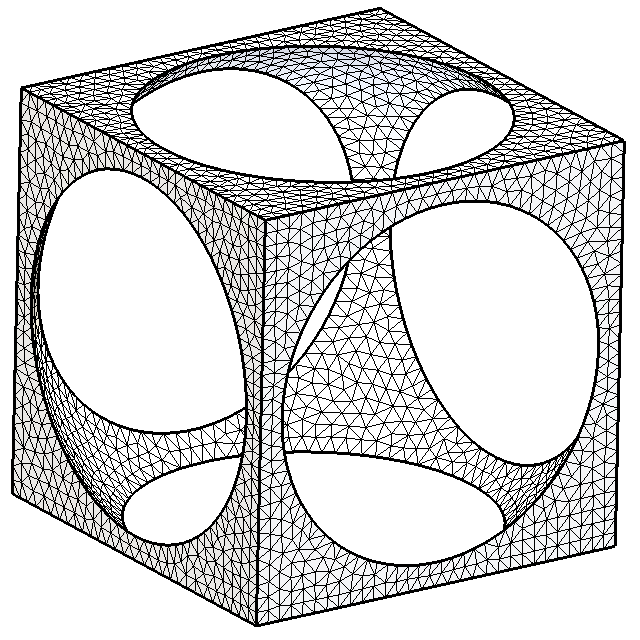
It is shown how adding forces responsible for reducing tetrahedral shape distortion eliminates flat tetrahedra. Sharp features are kept intact and resulting mesh is still Delaunay one.


Animation shows how sharp edges eventually appear on the boundary during elastic network self-organization.




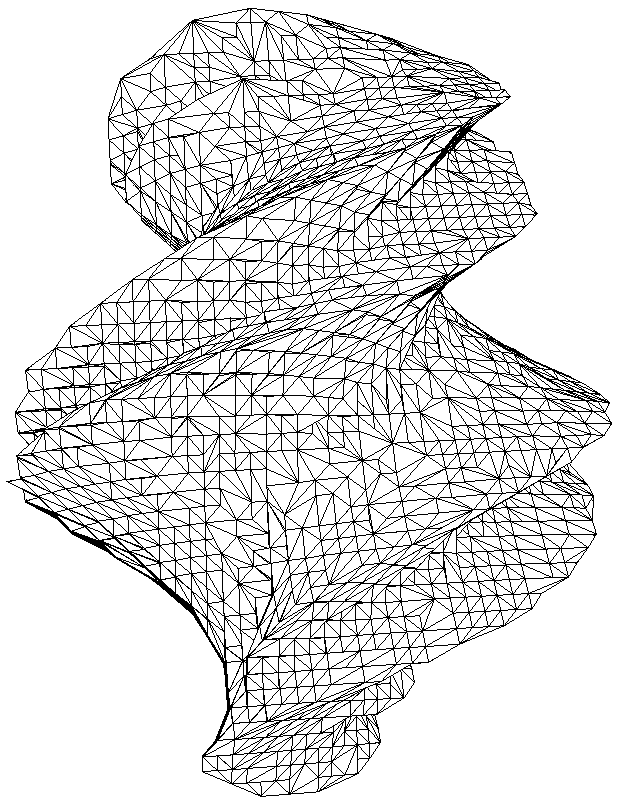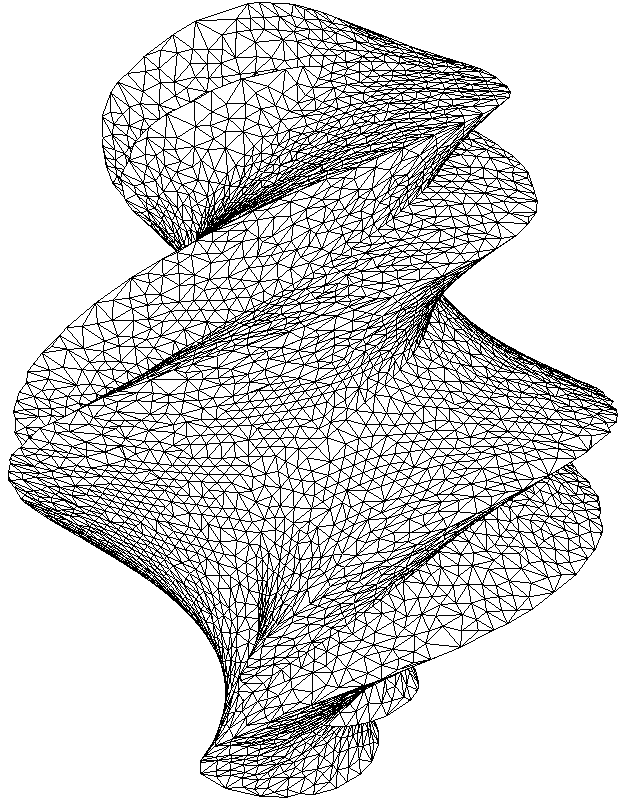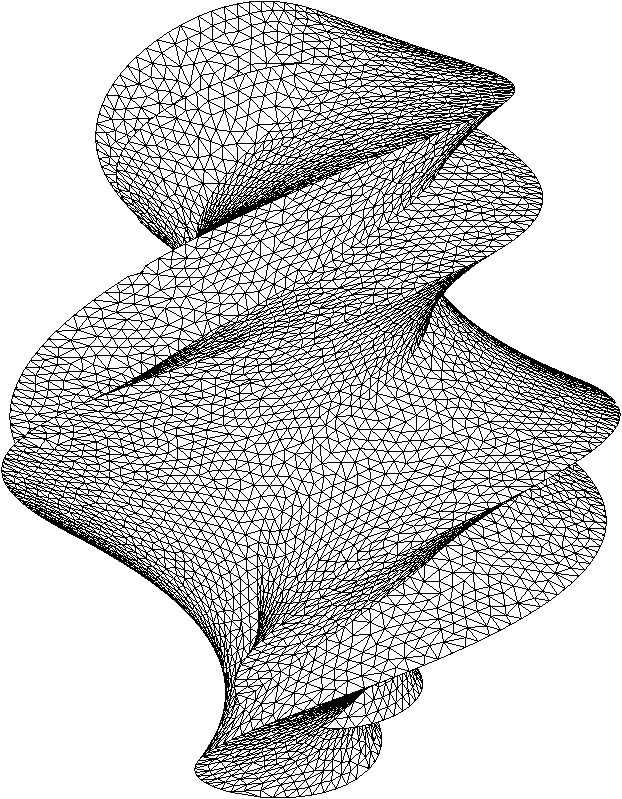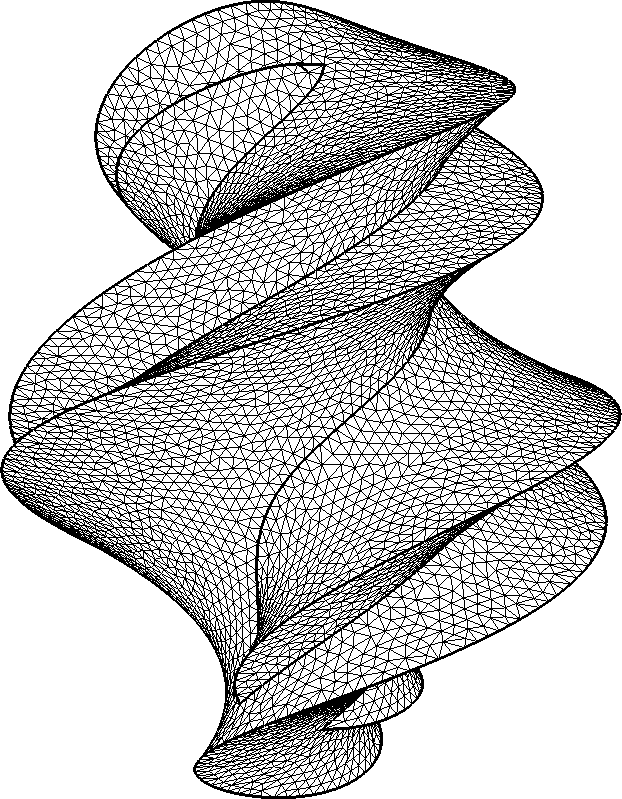
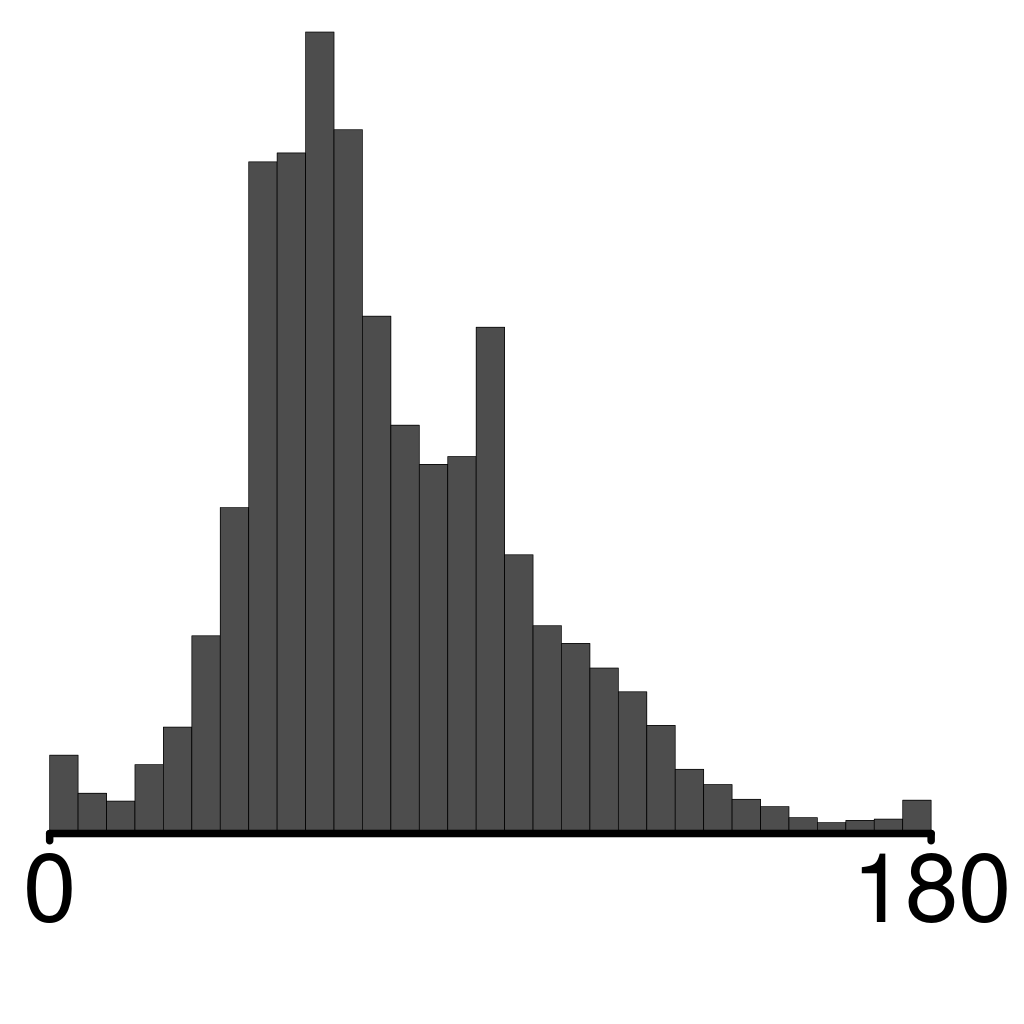
Resulting tetrahedral mesh quality is high enough. It can be used to construct approximately dual polyhedral mesh. Note the the body is defined analitically as a boolean combination of primitives.


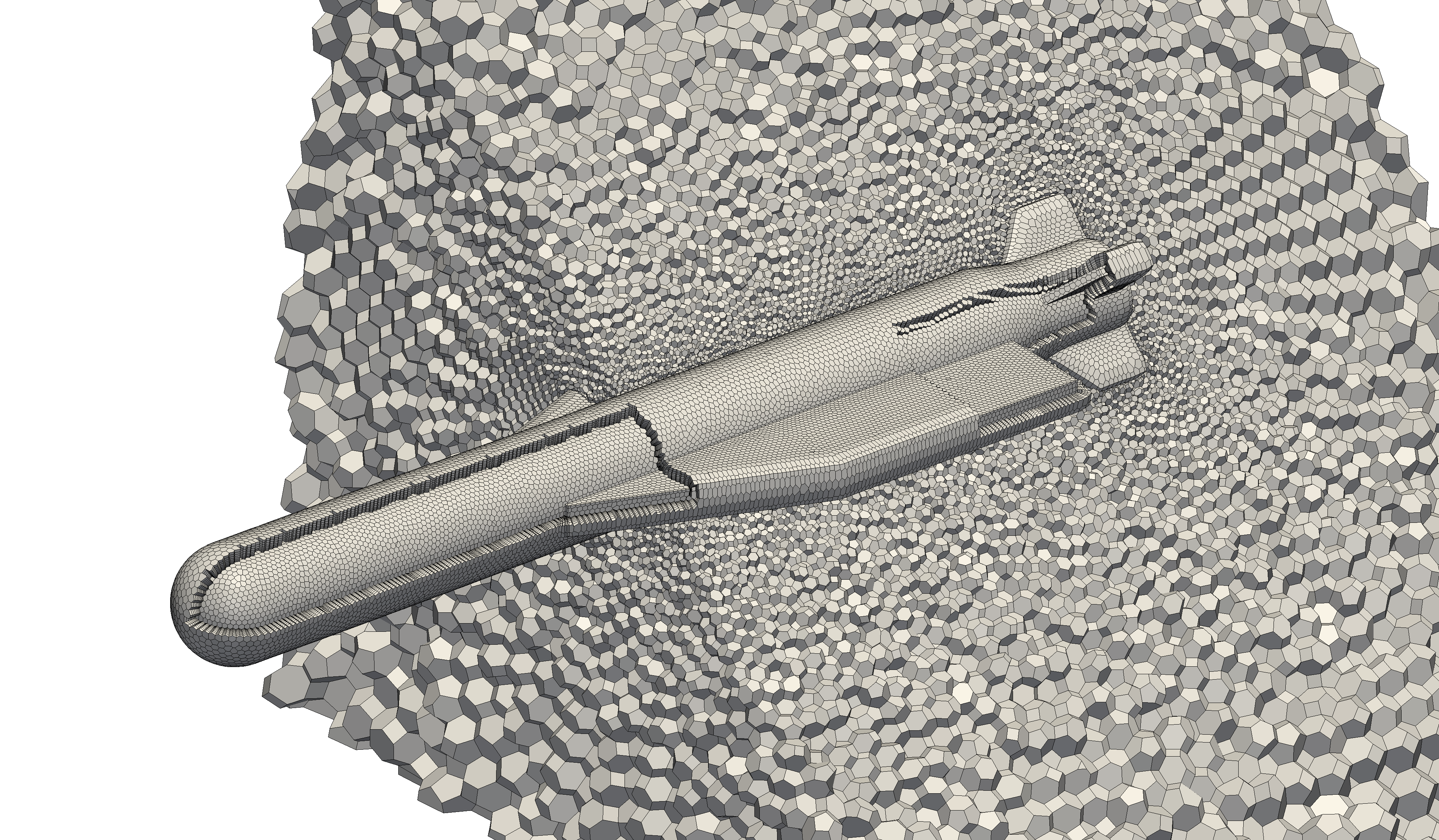
Объединяя призматический генератор с тераэдральным, получаем генератор гибридных сеток.


На основе такой сетки строится гибридная сетка из полиэдров со слоем полигональных призм около тела.