group homepage                                                                                                          Russian version

  Project smesher: generator of single block and multiblock aggregated meshes around winged bodies.

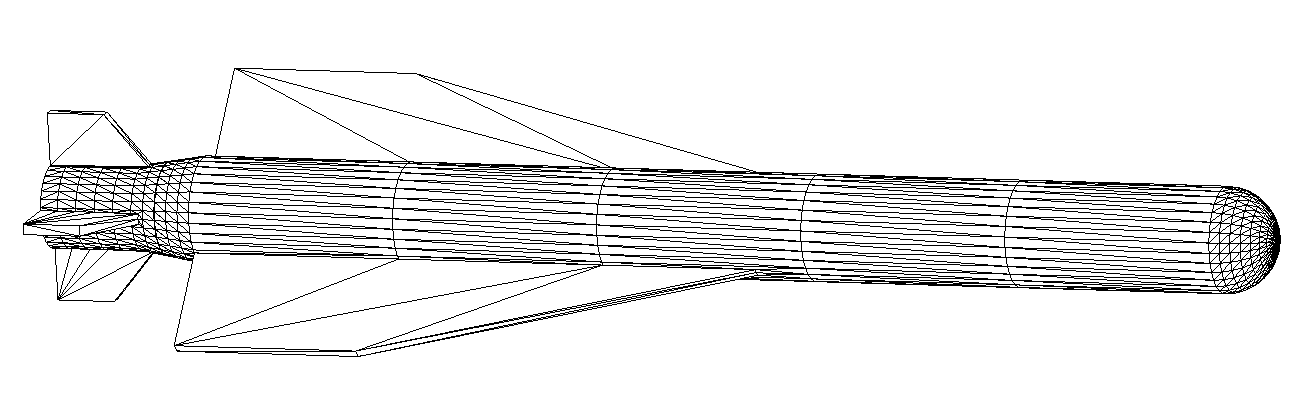
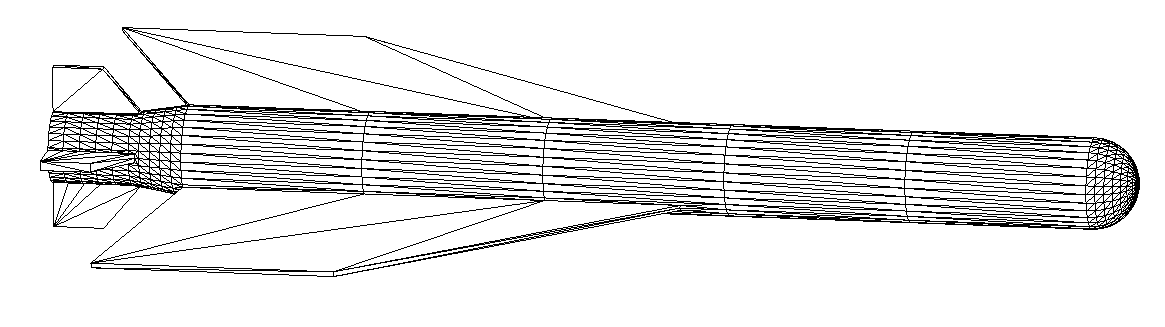
1) Model and initial tesselation.



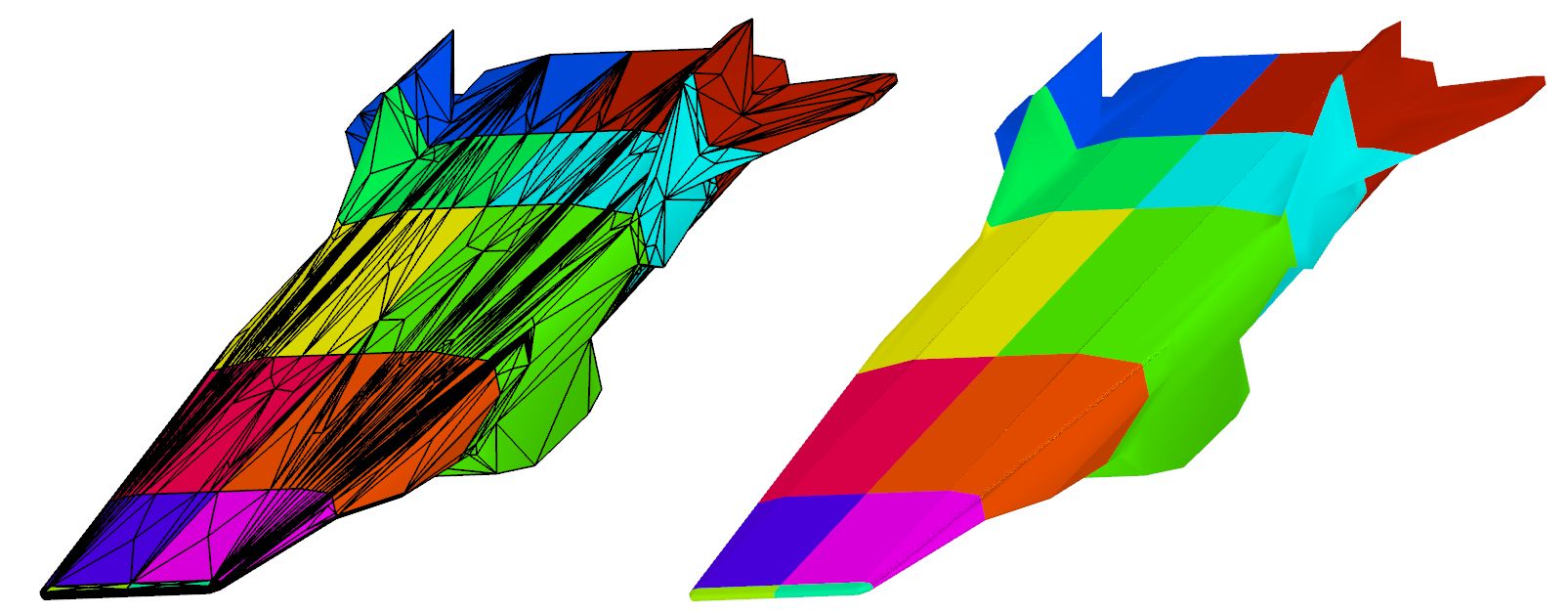
2) Fragment of tesselated surface and curvilinear surface mesh.
 

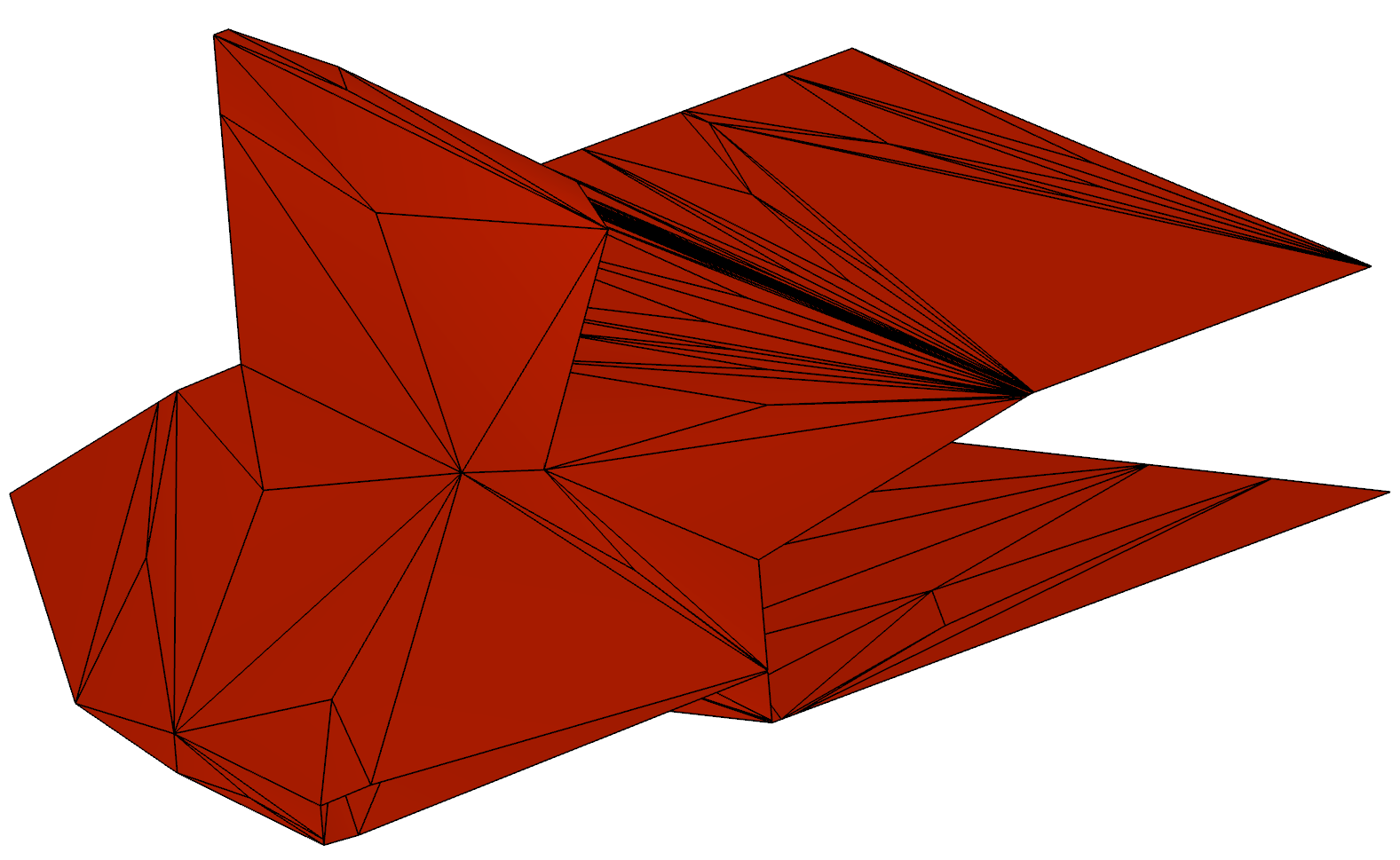
3) Adaptive untangling and optimization of 3d meshes. Algebraic initial guess is constructed, active zone around bad cells is marked and iterative untangling is applied locally. As soon as number of bad cells is reduced by factor 100, active zone is recomputed. For this test case active zone is recomputed four times in order to untangle global mesh.


 

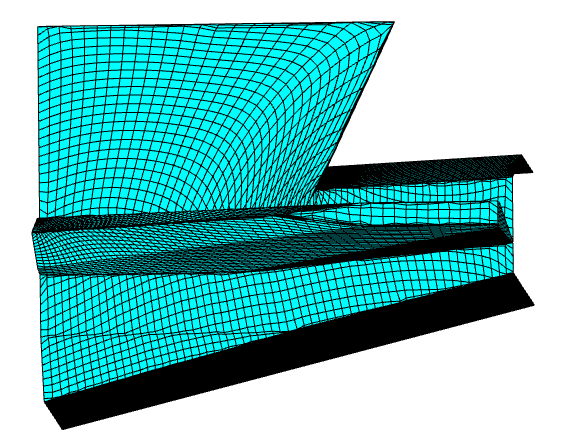
Example of adaptive surface mesh. Adaptation does not lead to cell skewing for anisotropic cells.

  

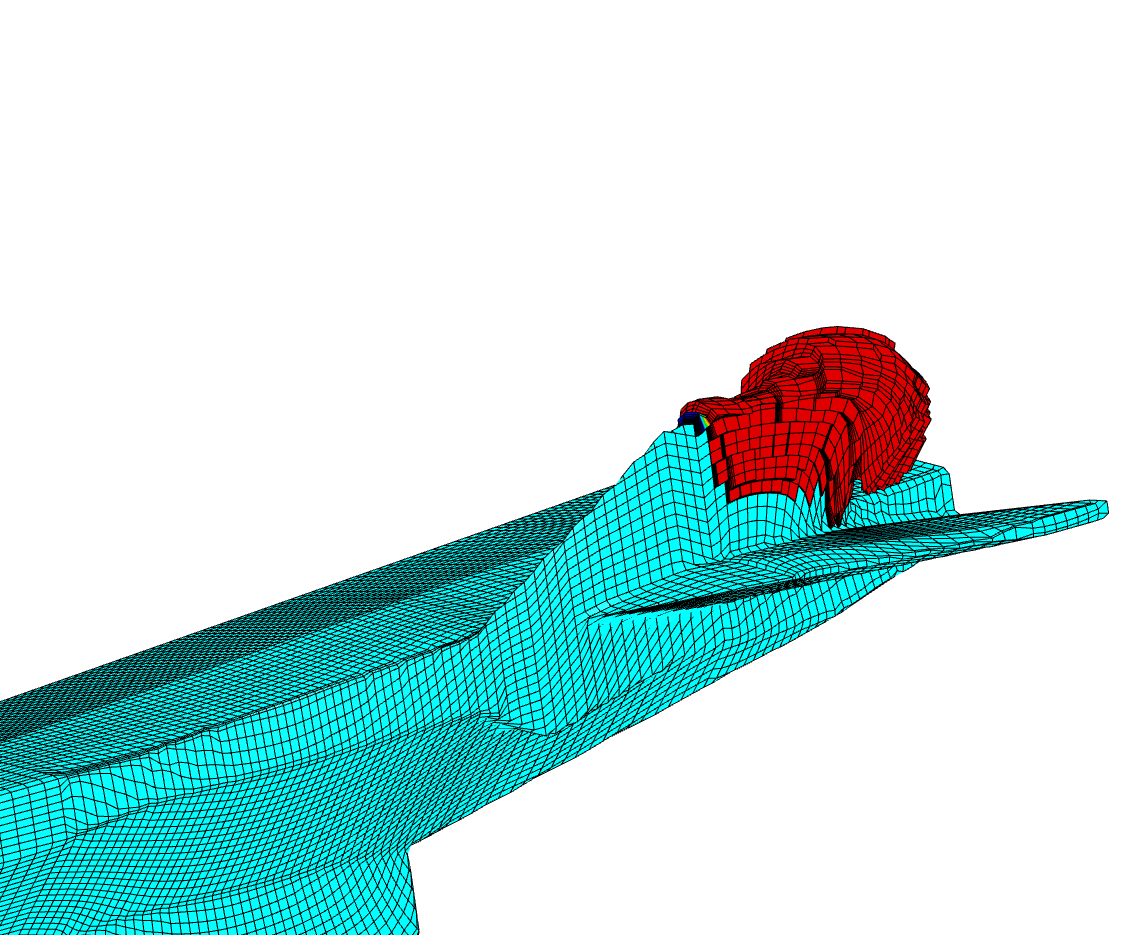
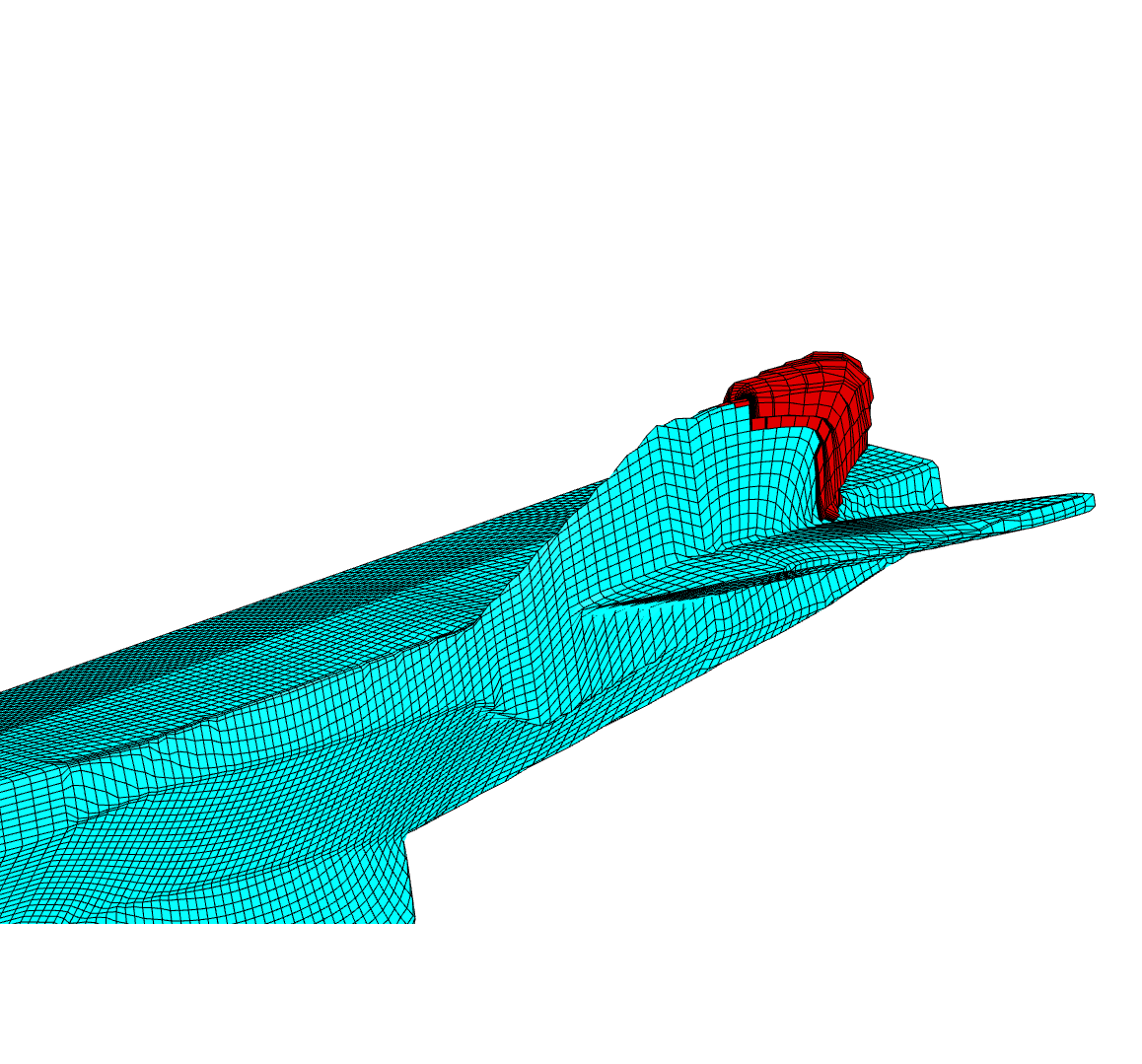
3d mesh around body and its refined version.

 


Meshing of simplified winged bodies. Initial teselation and final uniform monoblock structured mesh is shown. Curvature adaptation is not applied.



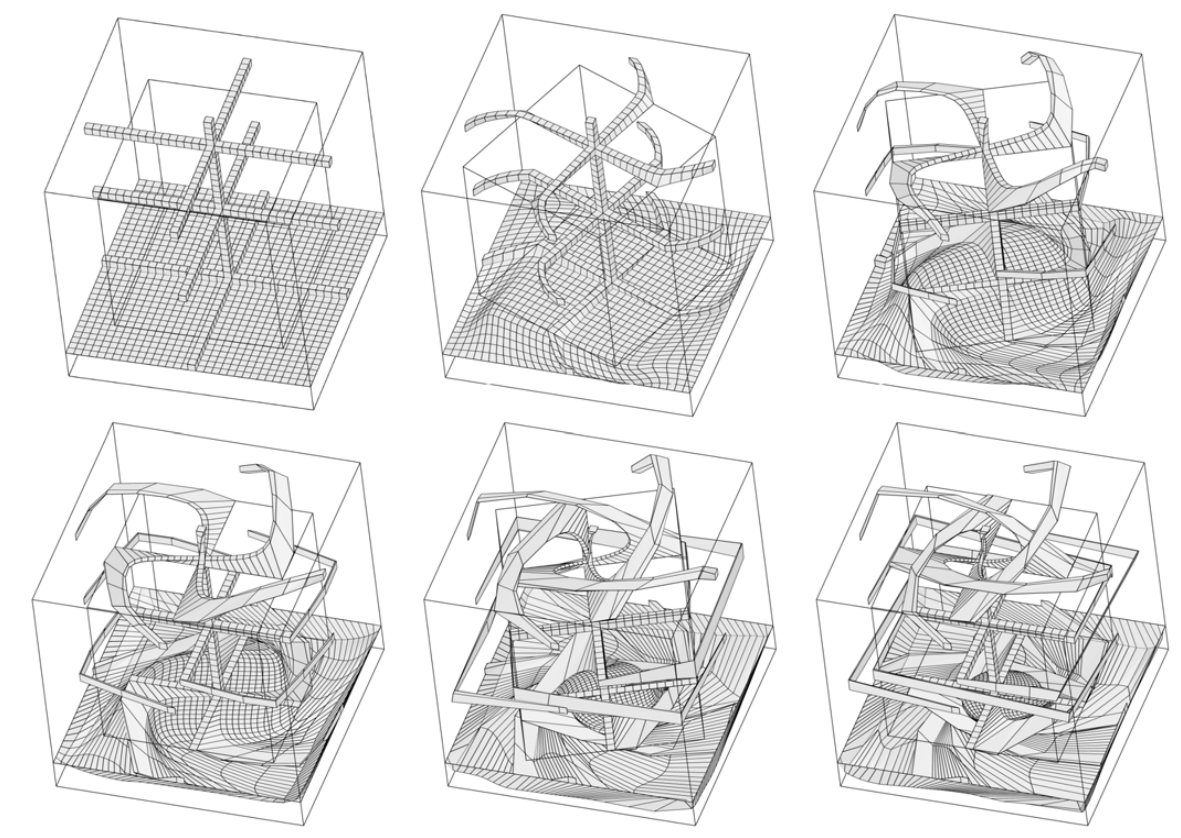
Example of mesh untangling in deformed geometry. Inner undeformed cube is rotated inside larger cube around vertical axis. Material  between two cubes is hyperelastic one. Rotation angles 0, pi/8,  3 pi / 8, pi/2, 7 \pi / 8, pi are considered. Continuation procedure for nonsingular deformation here is impossible since inner cube is intersects outer one when angle is large enough. The untangling results are shown. The rows of deformed hexahedral cells are images of rows made from the cubes under deformation. In all test untangling was succesfull.




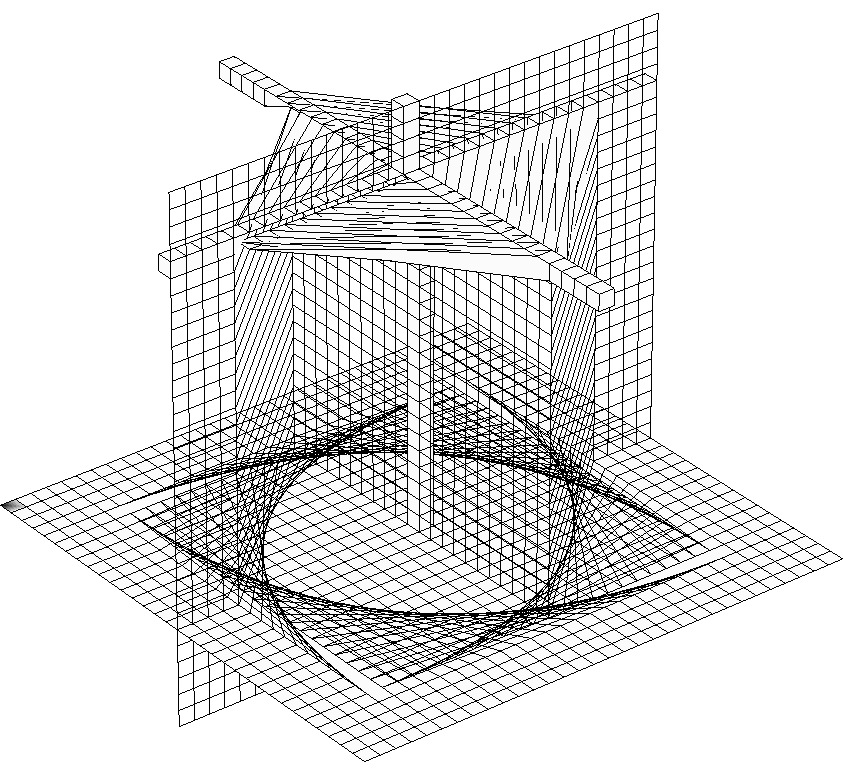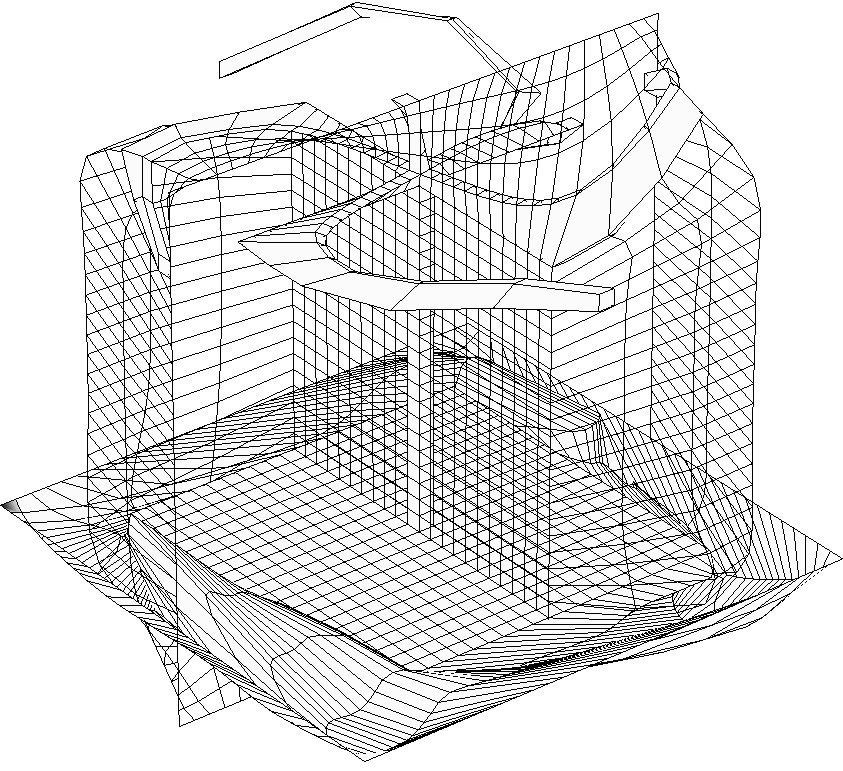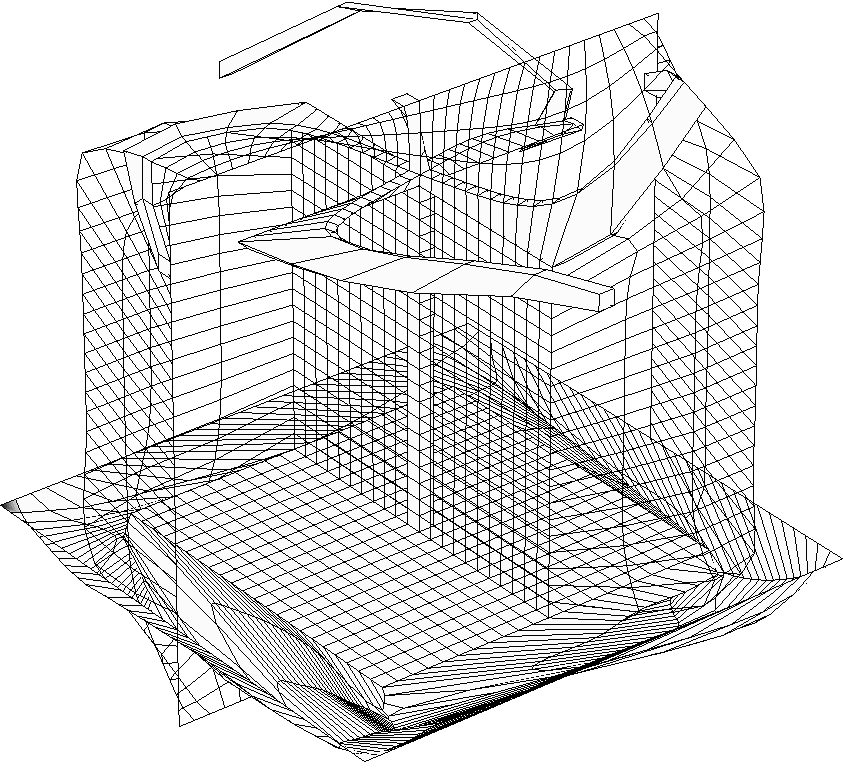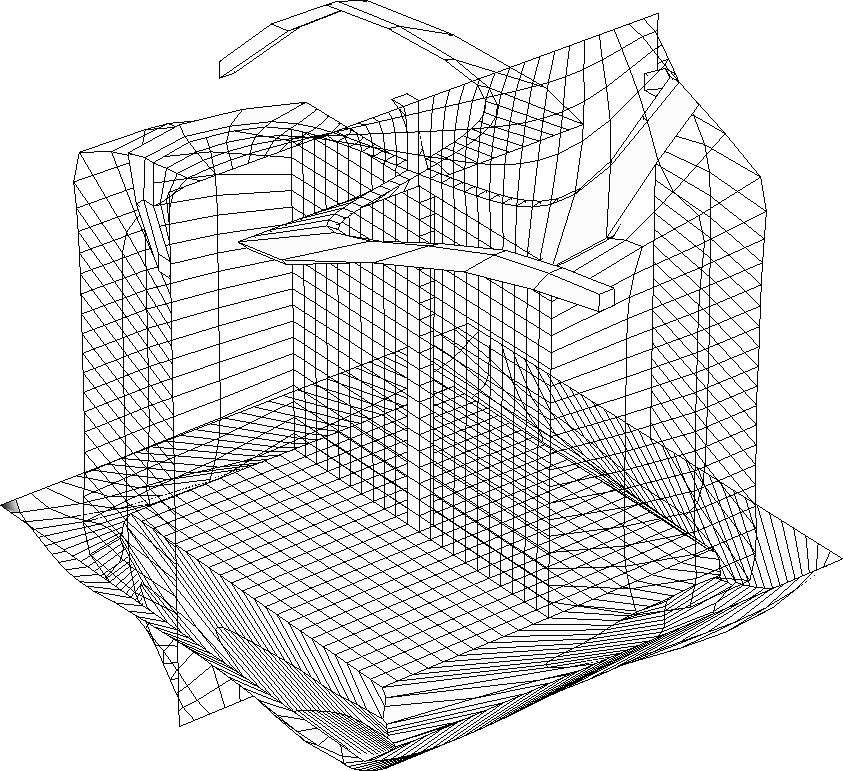
Behaviour of coordinate surface which is horizontal in original cube and passes through central stiff cube.





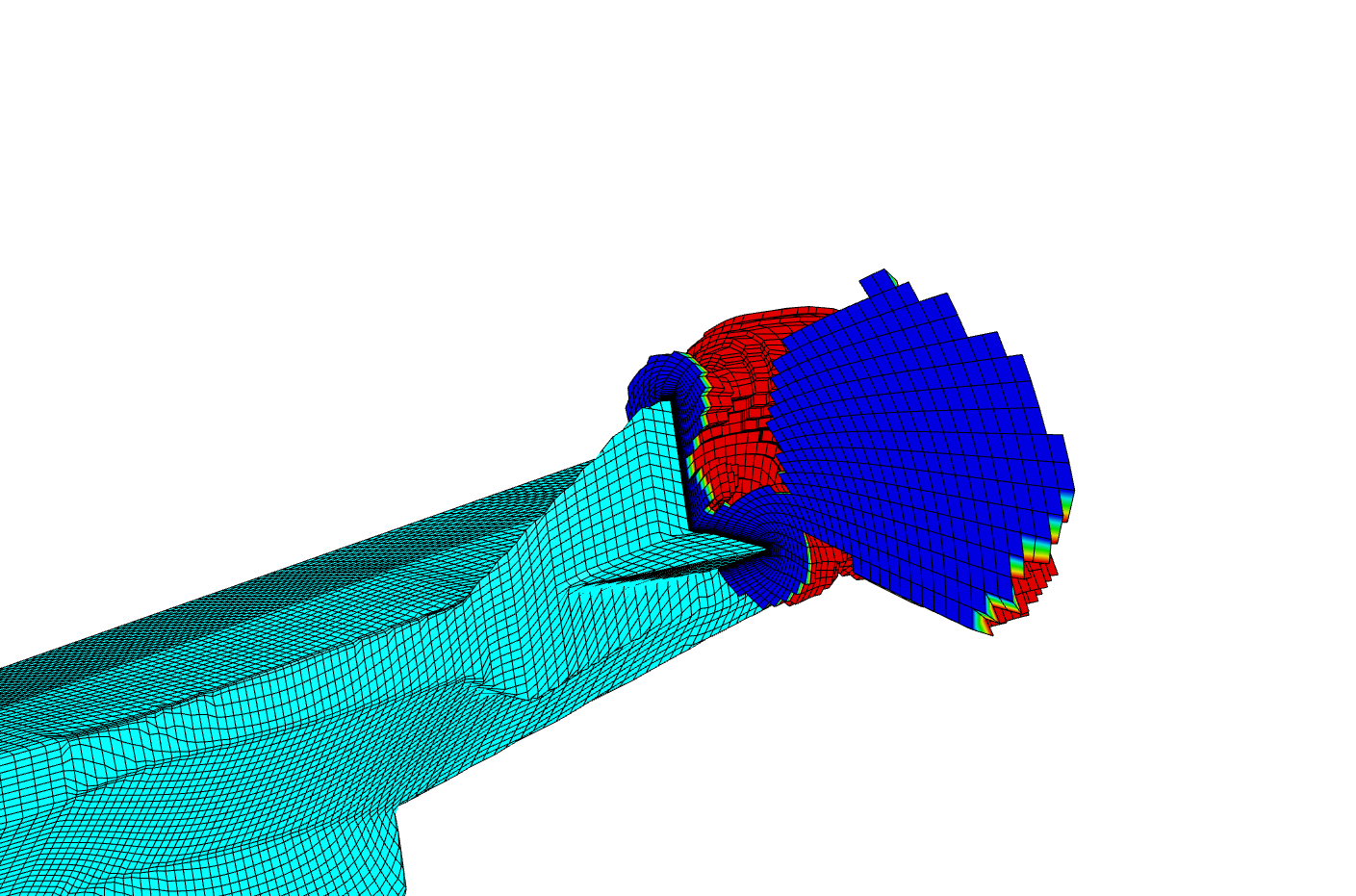
Example of tet mesh untangling after strong deformation of rotor blades.



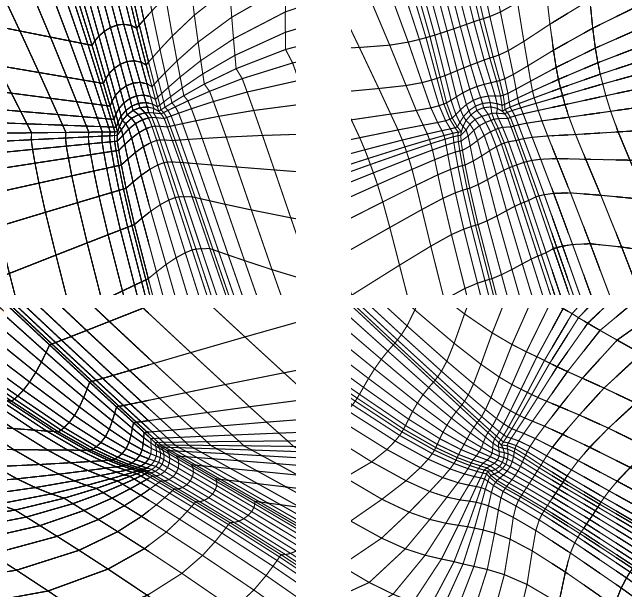
Mesh smoothing and orthogonalization in the key zones: near boundary layers and subdomain boundaries. Example of coordinate surface of block structured mesh of  H-type. Left - block structured mesh constructed using combination of algebraic and elliptic generator. Right - variational smoothing and orthogonalization.