The multi-indentation problem of rigid bodies of arbitrary shapes on a viscoelastic half-space.

Back to Kozhevnikov's page.

The contact between a tyre and a road is mainly modeled in the frame of the elastic theory. Generally, the viscoelastic effects have not been taken into account for computing the pressure distribution. But in fact the dynamic modulus of rubber is frequency dependent and the viscoelastic part can be more important than the elastic modulus. The experimental studies of dynamical tyre/road contact show that the contact areas obtained during rolling were smaller than in static conditions, that is mainly explained by the dynamical properties of tyre compounds, like the viscoelastic behaviour of the rubber. So the aim of our work is to propose a new numerical method for problems of multi-indentation on a viscoelastic half-space with asperities of arbitrary shapes for an increasing and then decreasing vertical loading.

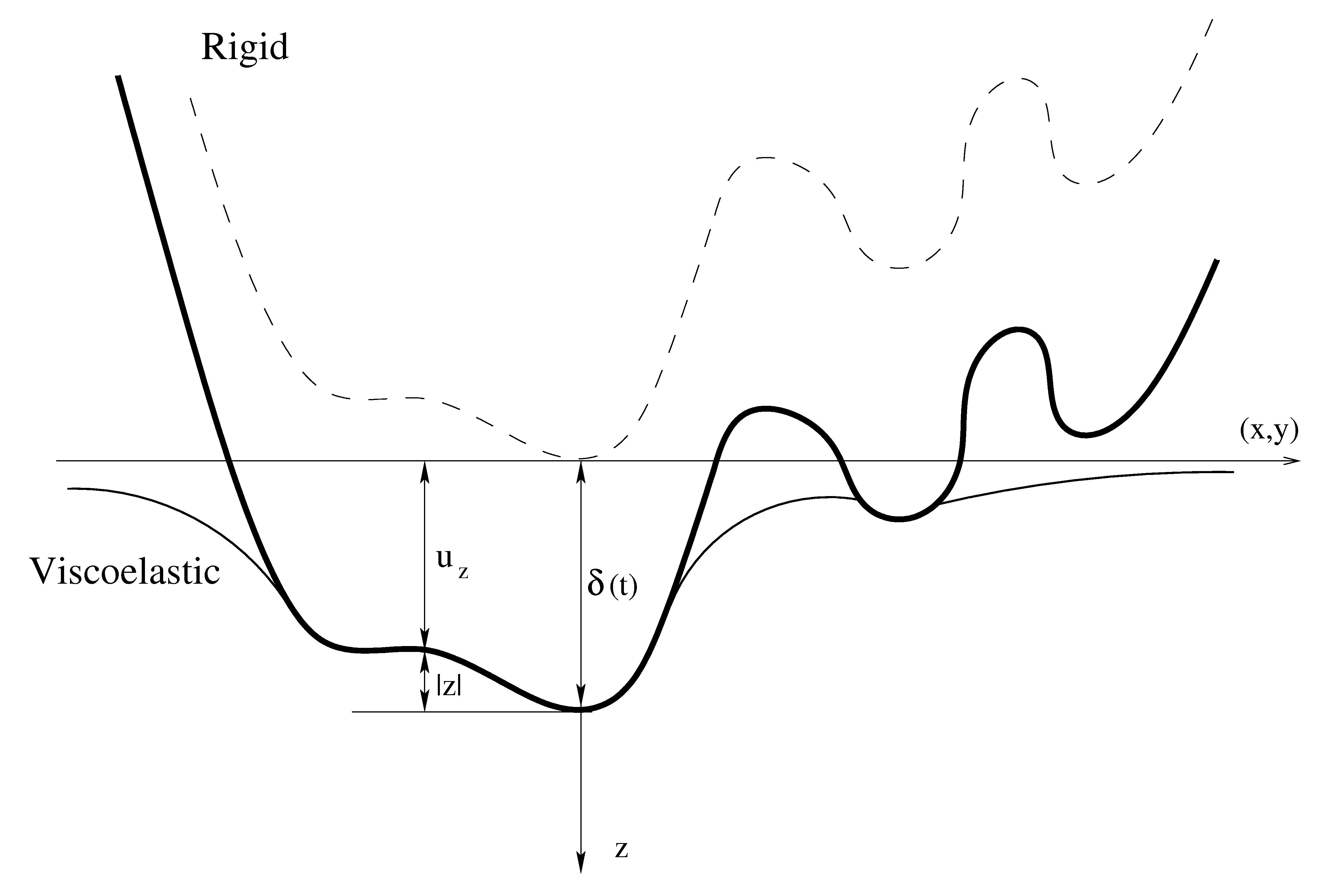
The contact problem between rigid indenters (micro asperities of the road) of arbitrary shapes and a viscoelastic half-space (tyre) is considered. Under the action of a normal force the penetration of the indenters changes and a few contact areas appeared.

The contact between a rigid indenter of arbitrary shape and

a viscoelastic half-space

We wish to find the relations which link the pressure distribution, the resultant forces on the indenters and the penetration on the assumption that the surfaces are frictionless. For indenters of arbitrary shapes the problem may be solved numerically by using the Matrix Inversion Method (MIM), extended to viscoelastic cases. In this method the boundary conditions are satisfied exactly at specified "matching points" (the mid-points of the boundary elements). 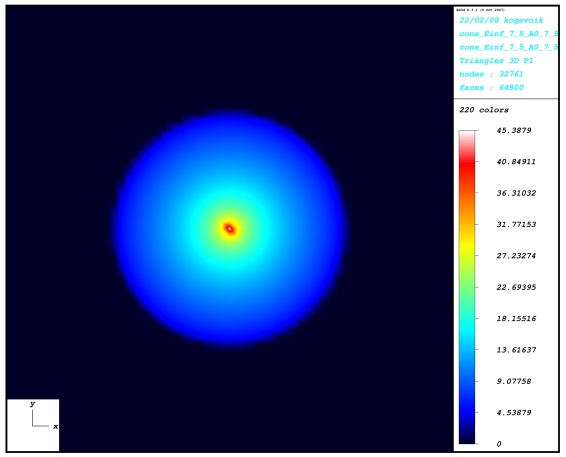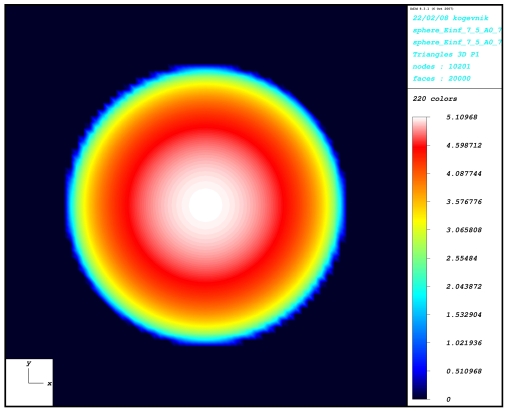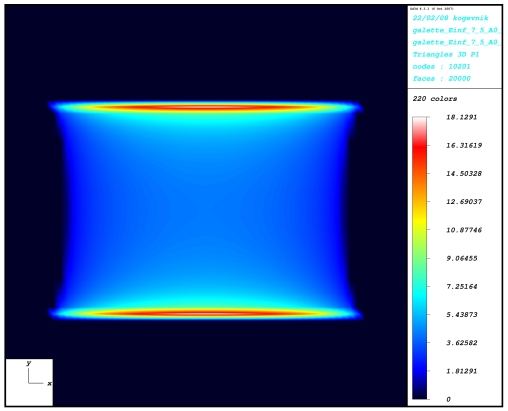It can be validated by comparing the numerical results to the analytic solutions in cases of a spherical asperity (loading and unloading) and a conical asperity (loading only). The pressure distribution and the contact area are found for a single spherical, conical and cylindrical indenter.

the conical indenter	the spherical-ended cylindrical indenter	the cylindrical indenter

When the problem involves a large number of points the MIM can become very time-consuming. Here the problem is solved using an alternative scheme, called the Two-scale Iterative Method (TIM). In this method the Local Matrix Inversion Method is used at the micro-scale for each contact area to compute the pressure distribution taking into account interacting effect (the forces on the other contact areas which can be calculated at the macro-scale) between indenters. Two algorithms were proposed. The first algorithm takes into account the distribution of forces on the other contact areas and the second is the approximation of the first algorithm and takes into account the resultant forces on the other contact areas. The method was implemented for a simple configuration of seven spherical indenters, seven spherical-ended cylindrical indenters and seven flat-ended cylindrical indenters as well as for a more complex configuration of twelve randomly positioned indenters of arbitrary shapes. For all these cases the TIM permits to find the pressure distribution and the contact forces versus the penetration. It can be validated by comparing the numerical results to the numerical results obtained with the MIM. The TIM was also validated by comparing to the Finite Elements Method (FEM) and to the measured data.

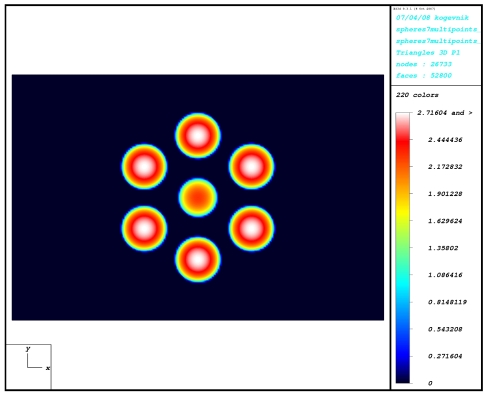
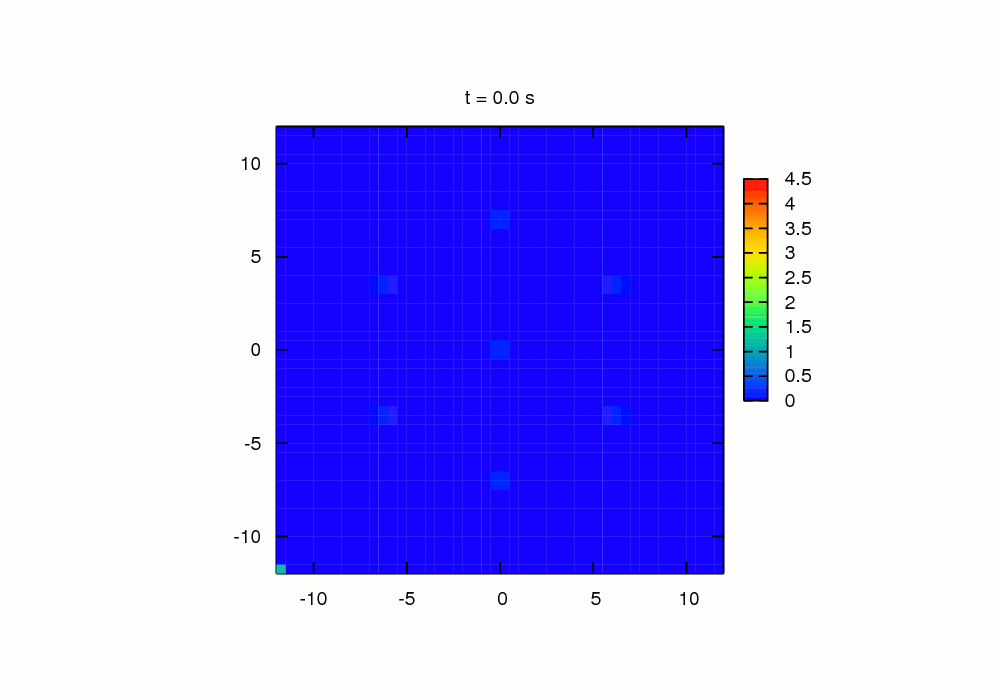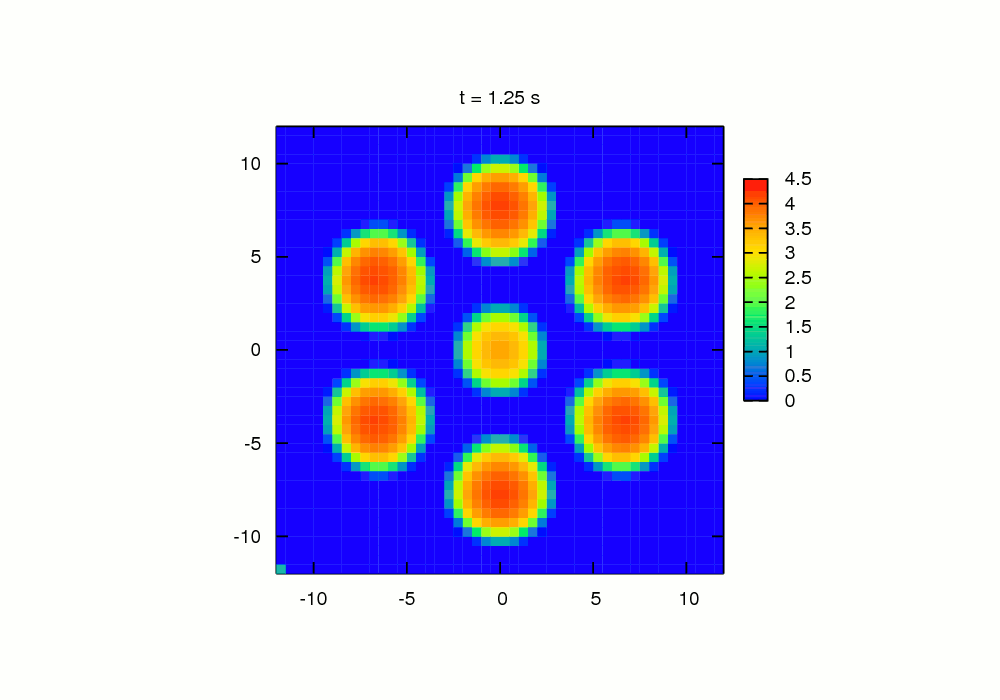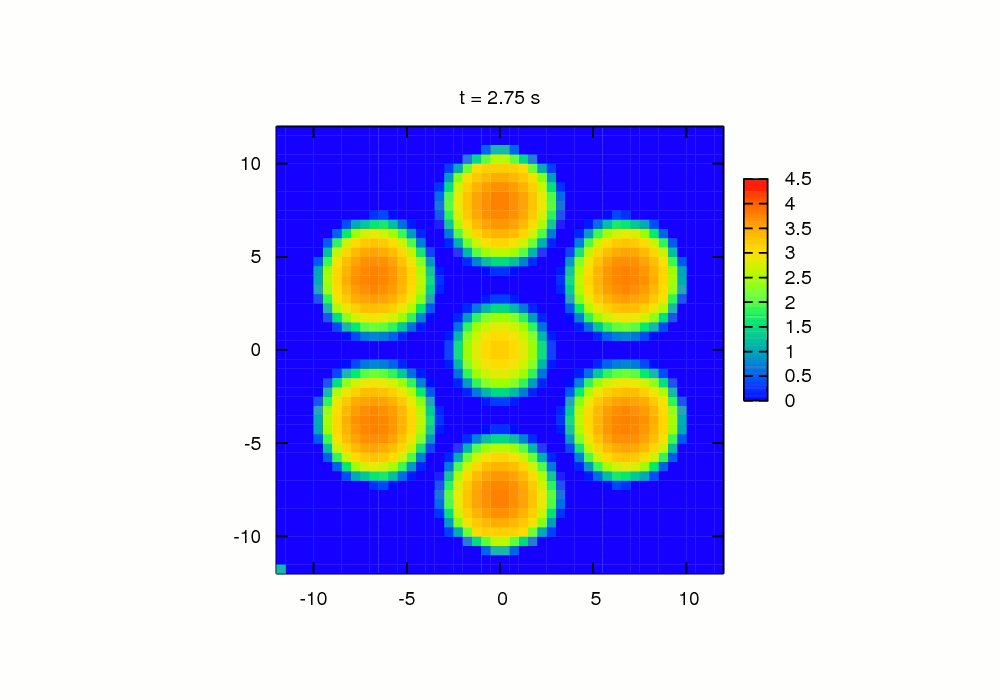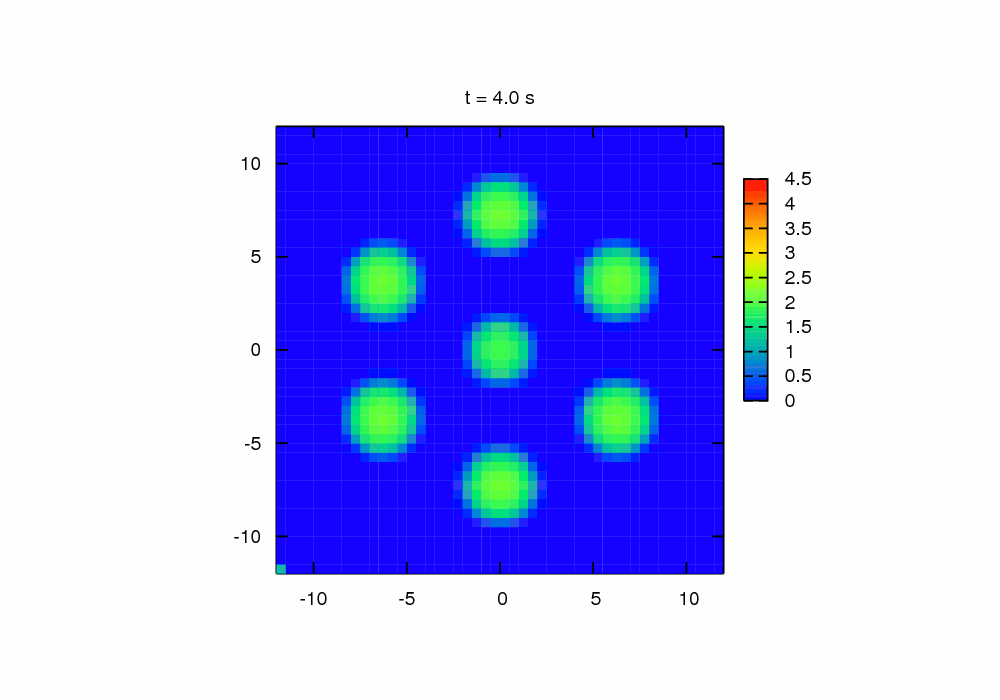
The indentation of a viscoelastic half-space by

seven rigid spherical-ended cylindrical indenters (Algorithm 2)

For a simple configuration of seven spherical-ended cylindrical indenters one can see the difference between the forces for central and peripheral indenters. The peripheral indenters deform the viscoelastic half-space under the central indenter and the contact force for the central indenter is less than for the peripheral indenters and the peripheral contact areas are larger than the central contact area.

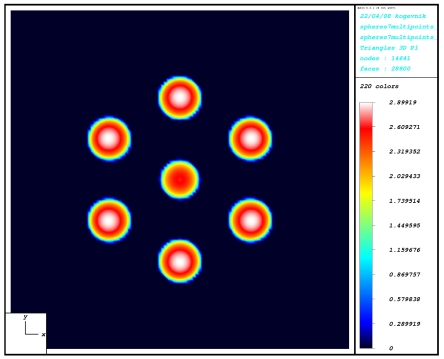
The indentation of a viscoelastic half-space by seven rigid spherical-ended cylindrical indenters (Algorithm 1)

Algorithm 1 catches better the influence of the central indenter on the peripheral indenters. Under the influence of the central indenter the maximum value of pressure shifts outside and no more in the tip of the peripheral indenter. Thus, one can see the asymmetry of the distribution of the pressure for peripheral indenters.

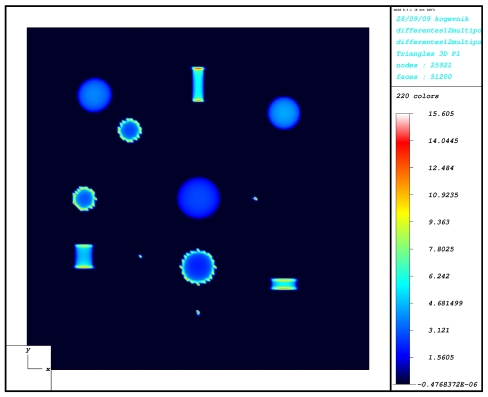
Now we consider the more general case of twelve indenters of arbitrary shapes. This configuration is composed of three rigid spherical-ended cylindrical indenters, of three flat-ended cylindrical indenters, of three conical indenters and of three cylindrical indenters (finite cylindrical shape with its curved face). This case is more complex since the indenting geometry doesn't have an axisymmetric profile and the positions of indenters are arbitrarily.

General case: three spherical-ended cylindrical indenters, three flat-ended cylindrical indenters, three conical indenters, three cylindrical indenters (Algorithm 1)

The maximum pressure for flat-ended cylindrical indenters is concentrated at the boundaries of each contact area. The maximum pressure for cylindrical indenters is concentrated at the boundaries of the contact area which are perpendicular to the axis y which is the axis of symmetry of the cylinder. The maximum pressures for cylindrical and flat-ended cylindrical indenters are comparable and the distributions are not symmetric. The maximum pressure for spherical-ended cylindrical indenters is less than for the others indenters. The absolute maximum pressure is on the conical indenters, but the contact areas are the smallest.

The last example of twelve randomly positioned indenters of arbitrary shapes shows that the proposed method could be probably applied to practical contact problems with a large number of asperities, such as for tyre-road contact computations.

Back to Kozhevnikov's page.