Alexander A

VIRTUAL GEOMETRY OF NATURAL NUMBERS. ALEXANDER A. ZENKIN, ANTON A.ZENKIN Computing Center of the Russian Academy of Sciences alexzen@com2com.ru

FOUNDATIONS OF THE NATURAL PYTHOGRAPHY

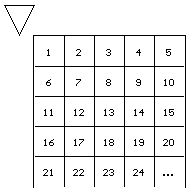
Consider the most ancient mathematical object - the well-known, monotonically increasing 1D-series of the common finite Natural Numbers:

1, 2, 3, 4, 5, 6, 7, . . . (I)

Rewrite the quite "boring" 1D-sequence (I) in the following 2D-form:

Fig.1. 2D-notation of the 1D-series (I).

It is evident that the number of strings in such the 2D-form of the series (I) is infinte.
Consider, further, any property of Natural Numbers, say, a predicate P(n) given on the 1D-set (I) or, that is now the same, on the 2D-table. For example, consider the quite "trivial" set of natural squares:

1, 4, 9, 16, 25, . . . (II)

and the predicat "to be or not to be a square of a natural number" or, more precisely:

P(n) = " n is a square of a natural number". Further, we shall paint over the cells of that 2D-table according to the rule: if P(n) is TRUE than the colour is, say, BLACK, else if P(n) is FALSE - then the color is, say, YELLOW:

It is natural that the colors are choiced arbitrary by our aesthetic liking.

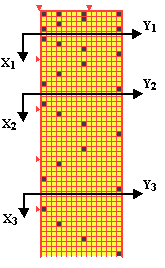
So, we obtain the following color-musical 2D-image (so-called PYTHOGRAM after Great Pythagoras) of a quite abstract mathematical property "to be or not to be a square of a natural number" (unfortunately, we are forced to leave hear a beautiful, mathematical pythograms' Music off screen ):

Fig. 2.

MAIN PROPERTIES OF THE PYTHOGRAMS.

     1. Quantity of numbers-cells in every string of that 2D-table is called the MODULUS (further - mod) of the pythogram.
     2. The pythogram, as a whole, visualizes the twice abstract CONNECTION between the additivity and multiplicativity properties of Natural Numbers: BTW, the ADDITIVITY of Natural Numbers is modelled by its COLOUR, the MULTIPLICATIVITY of Natural Numbers is modelled by their POSITION in the pythogram, since all numbers n, for which n = k x mod + j, j < mod, holds, are placed in the same j-th column of the pythogram.
     3. According to the quite cogent argument of known number theorists (Delone, Khinchin, etc.), main features of Number Theory problems are defined just that twice abstract CONNECTION between the additivity and multiplicativity properties of Natural Numbers. Therefore, as a rule (but not always), we shall be interested in not concrete properties of individual Natural Numbers, but just color-musical pythograms of that twice abstract CONNECTION as a whole ("ornamental patterns").

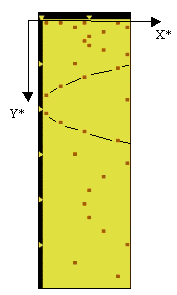
MAIN VISUAL TRANSFORMATIONS OF THE PYTHOGRAMS.

1. We shall change the physical SIZE of pythogram cells ad liberum (by our wish). For example, we can decrease that size as follows :

Fig. 3.

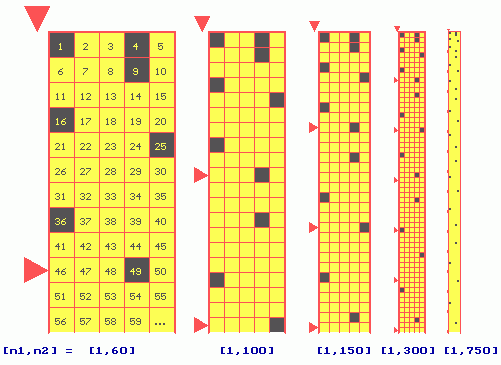
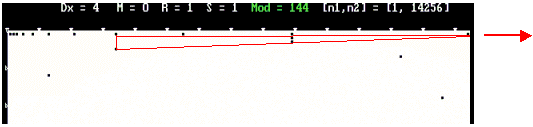
Such the trivial transformation allows essentially to increase the length of the segment of the series (I) that is visualized: here from [1,55] to [1,745].

Then, we can change a MODULUS of pythograms ad liberum (by our wish). For example, we can increase a modulus as follows :

Fig. 4.

The modulus of pythograms is a unique degree of (mathematical) freedom, which essentially enlarges the segment length of the serties (I) under consideration (here from 745 to 12218). It allows to see absolutely new mathematical structures generated by common Natural Numbers which (such the structures) do not exist and can't be seen in the linear form of the 1D-series (I):

Fig. 5. The length of the series (1) segment is equal to: L = [1, 21158]

The 11 stills only! From the trivial Fig 1 to the very non-trivial Fig 5, - and we have seen what a whole Mathematics was not seeing ever from the Pythagoras' time! Let us try to understand what we are seeing now.

NEW TYPE OF GEOMETRICAL OBJECTS: VIRTUAL PARABOLIC SOLITON RUNNING ALONG THE USUAL SERIES OF NATURAL NUMBERS.

In a far "bevore-computer" epoch, great Gotfried Leibniz supposed that "figures are useful to awake a thought". The modern computer CCG-technology open unique opportunities just for awaking a non-traditional and non-standard mathematical thought. We suggest some not quite ordinary examples.

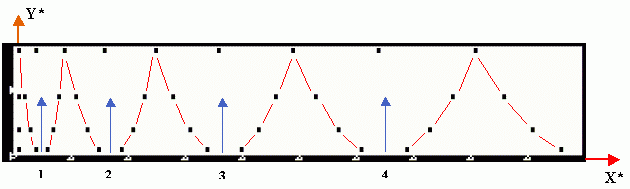
Let us try to understand the mathematical nature of some these visually-graphical structures. Successively changing the modulus of the phythogram, we create a color-musical movie, which at once prompts us the following unique VISUAL CCG-fact:

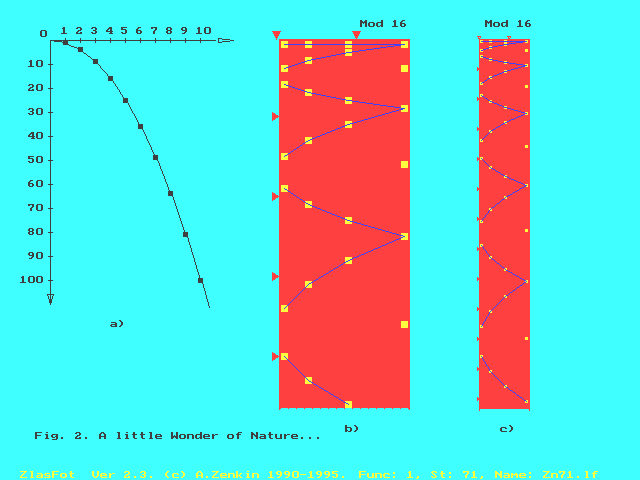
Fig. 6. The most beautiful and unexpected CCG-Discovery: traditional (a) and non-traditional (b,c) forms of the visual CCG-representation of the same mathematical object - of the well-known natural squares set, {1, 4, 9, 16, 25, 36, ...}. We have got a certain new “paradox” in modern mathematics: the distance between a) and b) figures is equal to ... about 2000 years! Indeed, even Pythagoras himself could draw b). Moreover, in 1841, Meobius drew very similar parabolas, - even just by the modulus 16 (!), - as a nomogram for multiplication of natural numbers in his known nomographical works. But only CCG-technique has allowed us to see, in the first time, this fantastic transformation! Indeed, the well-known ONE, but INFINITE, parabola is transformed into the INFINITE FAMILY but of FINITE parabolas! Such the transformation is not known in the modern Mathematics, and it brings to light new aspects of the eternal philosophical problem about a connection between the Finiteness and the Infiniteness.

ELEMENTARY MATHEMATICS OF THE INFINITY FAMILY OF THE FINITE PARABOLAS.

Fig. 7.

A quite not usual equation of a parabola in any n-th local coordinate system is as follows:

Y_n = (X_n /n)², X_n = 0, n, 2n, 3n, 4n; n = 1,2,3,… .

Fig. 8.

The equation of the infinite family of the finite parabolas in the coordinate of the CCG-space (Fig. 8) is as follows:

Y*(n) = ( 8 n ± k )² , k = 0, 1, 2, 3, 4; n = 0, 1, 2, . . . .

EXAMPLE. Let n=4, l = k - 8.

n=4

l -4 -3 -2 -1 0 1 2 3 4

8n+l 28 29 30 31 32 33 34 35 36

Theory 784 841 900 961 1024 1089 1156 1225 1296

Experiment 784 841 900 961 1024 1089 1156 1225 1296

So, here n is a parabola number; but the "value" of the function Y*(n) is not a usual number, but it is a sequence of the following NINE squares of successive natural numbers:
(8n-4)², (8n-3)², (8n-2)², (8n-1)², (8n)² , (8n+1)², (8n+2)², (8n+3)², (8n+4)²,

generating the n-th parabola for every n = 1, 2, 3, … .

Thus, a "point" (!) Y*(n) describes a whole GEOMETRIC object - the corresponding n-th parabola. In other word, that infinite family is simply the following sequence of finite 9-points parabolas:

Y*(0), Y*(1), Y*(2), . . . , Y*(n), . . . (III)

So, the sequence (III) is a sequence of NEW FINITE GEOMETRICAL OBJECTS that are VIRTUAL - in the common series (I), and are REAL - in the CCG-Space.

DYNAMICS OF VIRTUAL PARABOLIC SOLITONS PROPAGATING ALONG THE COMMON SERIES OF NATURAL NUMBERS.

Let us look at the following pythogram of the predicate "to be or not to be a square" under a successive change of its modulus. For example, let the mod be equal to 8, 9, 10, . . . 20.

Fig. 9.

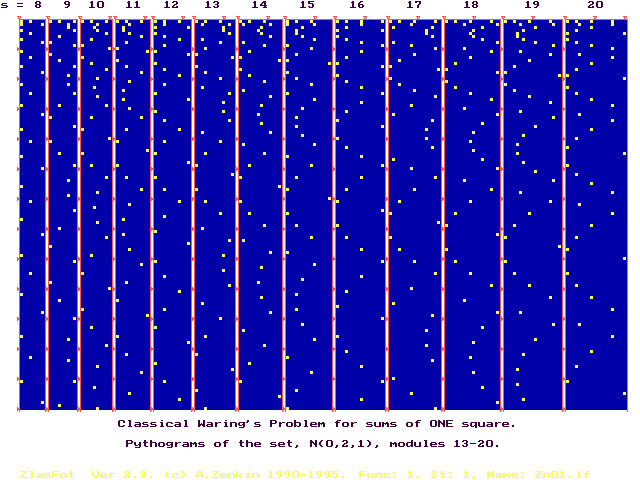
As it is easy to see (better, from right to left), some parabolas are jumping, others are moving down monotonically and dignifiedly.
Consider the last type of parabolas on the following pythogram modulo mod=18:

Fig. 10.

The equation of such the running parabola in the shown coordinate system is such:

Y* = (X* ± k)², k = 0,1,2, …, [sqrt (X*)], where X* = mod.

So, the function, Y*(X*) = Y*(mod), discribes and visually represents a REAL GEOMETRICAL object, - the finite parabola, - in every point X* = mod = 3, 4, 5, . . .

Fig. 11.

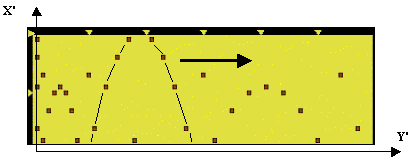
As is known, in Physics, an isolated, solitary wave is called a SOLITON.
So, our isolated, solitary parabolic wave in Fig. 11, is a PARABOLIC SOLITON, propagating along the integer axis Y' = 1, 2, 3, . . .,
No mathematician, from the Pythagoras' time, ever guessed that a lot of virtual geometrical objects of such the new type, the parabolic solitons, are running along the usual series of the common Natural Numbers during centures, and nobody saw them. Only CCG-approach allowed really to reveal such the DYNAMIC GEOMETRICAL OBJECTS in the Cognitive Reality of the CCG-Space.

On the jumping parabolas I shall tell you next time.

DYNAMICS OF VIRTUAL TRIANGLES PROPAGATING ALONG THE COMMON SERIES OF COMMON NATURAL NUMBERS.

MATHEMATICAL DISCOVERY OF THE PAINTER ALEXANDER F.PANKIN. From Great Leonardo's time the classical series of the Fibonacci's Numbers: {0, 1} 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . . . (IV)

attracts attention of artists, sculptors, architects, and so on.
On the 23 October, 1999, the known Russian painter Alexander Pankin, using CCG-Visualization approach, drew (without any computer!) some pythograms of initial segments of the Natural Numbers series (I) with the predicate:

P(n) = " n is a Fibonacci Number", (1)

and HAVE SEEN the following (see Fig. 12)

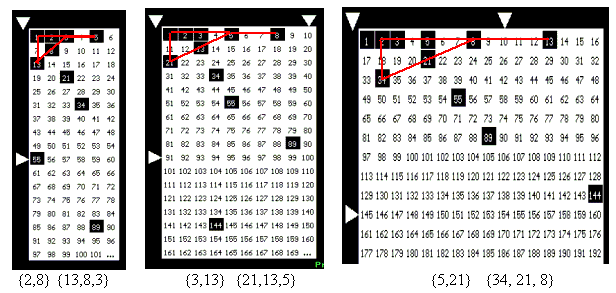
VISUAL FACT 1. The threes of Fibonacii's Numbers (21,13,5), (34,21,8), and (55,34,13) make up straight lines, and the threes of Fibonacii's Numbers (3,8,13), (5,13,21), and (8,21,34) are placed in one column.

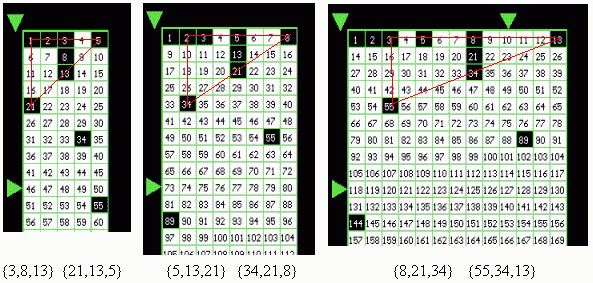
Fig. 12. Pythograms of initial segments of Natural Numbers Series (I) with the predicate (1). The modules of these pythograms are equal to the Fibonacci's Numbers 5, 8, and 13, correspondingly.

Then he came out with a HYPOTHSIS that such the property holds for ALL pythograms of such the kind. Our CCG-System confirmed that the Pankin's hypothesis is very plausible (see Fig. 13 and 14).

Fig. 13.

Fig. 14
Since Mathematics takes on trust nothing, this visual hypothesis was proved next day.

SOME NEW GEOMETRICAL PROPERTIES OF THE FIBONACCI NUMBERS. MATHEMATICAL "THEORY" I.

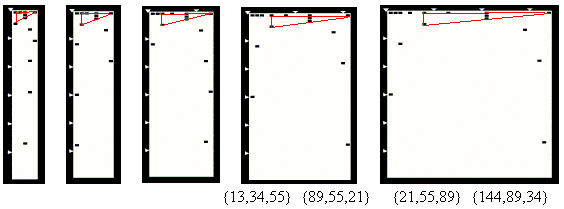
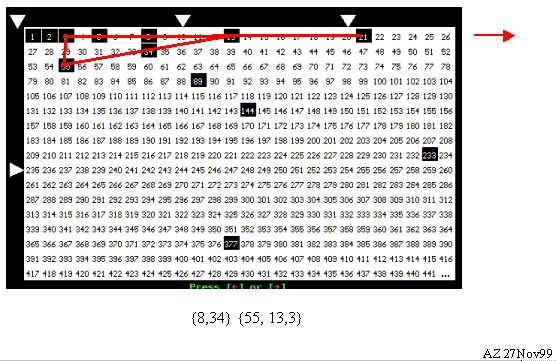
Consider ANY SEVEN of successive Fibonacci's Numbers {f₁, f₂, f₃, f₄, f₅, f₆, f₇, } and the corresponding pythogram modulo f₄ with the predicate (1). The pythogram modulo 13, presented in Fig. 15, illustrates the situation for the third seven {3,5,8,13,21,34,55}.

Fig. 15.

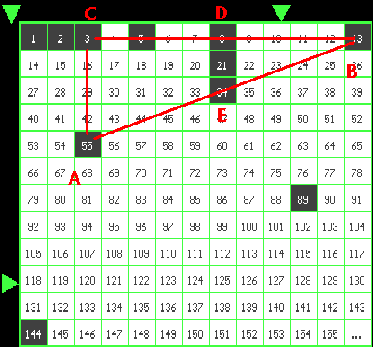
    Introduce the following designations.
    Local coordinate system connected with the triangle ABC:
    Origin: C(0,0); X-axis: the line CB; Y-axis: the line CA.

In this local coordinate system, the points A - E will have the following coordinates, expressed via Fibonacci's Numbers:

A(0,4), B(f₄- f₁ , 0), C(0 , 0), D(f₃- f₁ , 0), E(f₃- f₁ , 2).
Prove now some trivial geometrical statements.

THEOREM 1. THE POINT E LIES ON THE SIDE AB OF THE TRIANGLE ABC.

PROOF.

a) THE EQUATION OF THE LINE AB. From

(Y - Y_A )/( Y_B - Y_A ) = (X - X_A )/( X_B - X_A) and (Y - 4) / (-4) = X / (f₄- f₁), we have

4 X + (f₄- f₁) Y - 4 (f₄- f₁) = 0 (2)

b) From the definition itself of the Fibonacci's Numbers we have:

(f₃= f₄- f₂ ) & (f₃= f₂+ f₁) ® (2f₃= f₄+ f₁) ® (f₃= (f₄+ f₁)/2).

f₃- f₁ = (f₄+ f₁)/2 - f₁ = (f₄- f₁)/2.

c) Since E(f₃- f₁ , 2) = E((f₄- f₁ )/2, 2), we have for the point E from (2) :

4 (f₄- f₁ )/2 + (f₄- f₁) 2 - 4 (f₄- f₁) = 0.

So, the point E(f₃- f₁ , 2) really lies on the side AB of the triangle ABC.

THEOREM 2. FIBONACCI NUMBERS f₃, f₅, f₆ BELONG TO THE SAME COLUMN, f₃, OF THE PYTHOGRAM MODULO f₄, SO THAT THE NUMBERS f₃, f₅, f₆ ARE A MIGLINE OF THE TRIANGLE ABC.

PROOF. By the definition itself of the Fibonacci's Numbers, f₅ = f₄ + f₃, f₆= f₅+ f₄ = 2 f₄ + f₃. So, f₃, f₅ , f₆ = f₃ (mod f₄), i.e., the numbers f₃, f₅ , f₆ belong to the same column, f₃ , of the pythogram modulo f₄ and are placed in the strings 1,2,3, correspondingly. Since (f₃ - f₁= f₂) & (f₄ - f₃= f₂) and the columns with numbers f₁ and f₃are always parallel, the line made up by the numbers f₃, f₅ , f₆ is a midline of the rectangular triangle ABC.

MATHEMATICAL DISCOVERY OF THE CHEMIST VALERY A.NIKANOROV. On the 11 November, 1999, the known Russian chemist Valery Nikanorov, using CCG-approach, drew (without any computer!) some other pythograms of initial segments of the Natural Numbers series (I) with the same predicate:

P(n) = " n is a Fibonacci Number", (1)

and HAVE SEEN the following (see Fig. 16)

VISUAL FACT 2. The pythograms by modules 6, 10, 16, which are not Fibonacii's Numbers, have topologically invariant structure like "metyl-cyclopropan".

Fig. 16.

Then he came out with a HYPOTHSIS that such the property holds for ALL pythograms of such the kind. Our CCG-System confirmed that the Nikanorov's hypothesis is very plausible (see Fig. 17).

Fig. 17.

Since Mathematics takes on trust nothing, this visual hypothesis was proved next day.

SOME NEW GEOMETRICAL PROPERTIES OF THE FIBONACCI NUMBERS. MATHEMATICAL "THEORY" II. Consider ANY SEVEN of successive Fibonacci's Numbers {f₁, f₂, f₃, f₄, f₅, f₆, f₇, } and the corresponding pythogram modulo 2f₄ with the predicate (1). The pythogram modulo 16, presented in Fig. 18, illustrates the situation for the second seven {2,3,5,8,13,21,34}.

Fig. 18.      Introduce the following designations.
    Local coordinate system connected with the triangle ABC:
    Origin: C(0,0); X-axis: the line CB; Y-axis: the line CA.

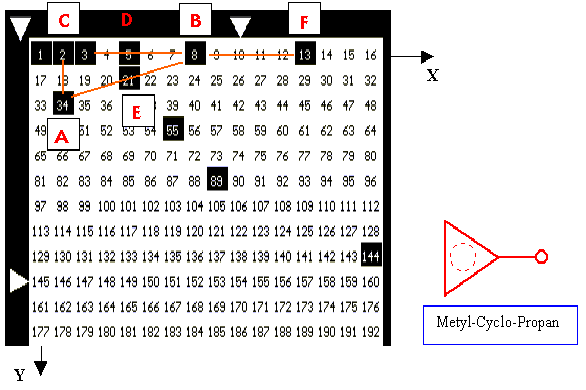
In this local coordinate system, the points A - F will have the following coordinates, expressed via Fibonacci's Numbers:

A(0,2), B(f₄- f₁ , 0), C(0, 0), D(f₃- f₁ , 0), E(f₃- f₁ , 1), F(f₅ - f₁ , 0).
    Prove now some trivial geometrical statemenets.

GIVEN:
    A SEVEN OF SUCCESSIVE FIBONACCI NUMBERS {f₁, f₂, f₃, f₄, f₅, f₆, f₇, };
    THE PYTHOGRAM MODULO 2 f₄, AND THE TRIANGLE ABС = {f₇, f₄, f₁, }

THEOREM 3. THE POINT E LIES ON THE SIDE AB OF THE TRIANGLE ABC.

PROOF. a) THE EQUATION OF THE LINE AB. From

(Y - Y_A )/( Y_B - Y_A ) = (X - X_A )/( X_B - X_A) and (Y - 2) / (-2) = X / (f₄- f₁), we have

2 X + (f₄- f₁) Y - 2 (f₄- f₁) = 0 (3)

b) From the definition itself of the Fibonacci's Numbers we have:

(f₃= f₄- f₂ ) & (f₃= f₂+ f₁) ® (2f₃= f₄+ f₁) ® (f₃= (f₄+ f₁)/2).

f₃- f₁ = (f₄+ f₁)/2 - f₁ = (f₄- f₁)/2.

c) Since E(f₃- f₁ , 1) = E((f₄- f₁ )/2, 1), we have for the point E from (3) :

2 (f₄- f₁ )/2 + (f₄- f₁) 1 - 2 (f₄- f₁) = 0.

So, the point E(f₃- f₁ , 1) really lies on the side AB of the triangle ABC.

THEOREM 4. FIBONACCI NUMBERS f₃ and f₆ BELONG TO THE SAME COLUMN, f₃, OF THE PYTHOGRAM MODULO 2f₄, SO THAT THE NUMBERS f₃ and f₆ ARE A MIGLINE OF THE TRIANGLE ABC.

PROOF. By the definition itself of the Fibonacci's Numbers, f₆= f₅+ f₄ = 2 f₄ + f₃. So, f₃, f₆ = f₃ (mod 2f₄), i.e., the numbers f₃and f₆ belong to the same column, f₃ , of the pythogram modulo 2f₄ and are placed in the strings 1 and 2, correspondingly.
Since (f₃ - f₁= f₂)& (f₄ - f₃= f₂) and the columns with numbers f₁ and f₃are always parallel, the line made up by the numbers f₃ and f₆ is a midline of the rectangular triangle ABC.

IMPORTANT REMARK.

The calssical series of Fibonacci's Numbers is generated by the initial pair {0,1}:

{0, 1} 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, . . . (IV)

All the Theorems proved above use the DEFINITION ONLY of the Fibonacci Numbers. Thefore they hold for the GENERALIZED FIBONACCI SERIES produced by any initial pair of integers {m,n}.

CONCLUSIONS VIRTUAL GEOMETRY OF NATURAL NUMBERS.

Now, let us return to the habitual, most ancient mathematical object that is investigated during about 5000 years, - to the usual series of the usual finite Natural Numbers:

1, 2, 3, 4, 5, 6, 7, . . . , n, . . . (I)

    But nobody, from Pythagoras' time, even guessed that there exists a stormy life of virtual FINITE GEOMETRICAL OBJECTS in this series (I). And only the CCG-technology of the cognitive-semantic visualization of mathematical abstractions has allowed to see such the objects and to understand some of their unexpected and wonderful mathematical properties.
     It's wonderful that some of these CCG-discoveries was made by non-professional mathematicians, but just a painter and a chemist (see above). That allows to state that our CCG-Technology is really an effective way to scientific discoveries.

    We believe that great Leopold Kronecker was right, a thousand times, saying

"Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk" And Great Henry Poincare did so: "All Mathematics can be produced from the conception of the Natural Number"

    Our today's CCG-results, concerning the Virual Geometry of Natural Numbers, can be presented in the next "2D-form".

BASIC MATHEMATICAL OBJECT GENERATING NUMBER-THEORETICAL SET NEW VIRTUAL GEOMETIRCAL OBJECTS

1 The Series of Natural Numbers (I) The set of squares of natural numbers (II): {1,4,9,16,25, . . .} Parabolic solitons, running along the series (I)

2 The Series of Natural Numbers (I) The set of (generalized) Fibonacci's Numbers (IV) Virtual Fibonacci's Triangles   jumping along the series (I)

3 The Series of Natural Numbers (I) ? ? ? ? ? ?

. . . . . . . . . . . .

     There arise some non-trivial questions.

WHAT A GENERATING SET WILL BE THE NEXT ONE ? WHAT NEW GEOMETRICAL OBJECTS WILL IT GENERATE ? WHETHER WE, INDEED, KNOW ALL AS TO THE COMMON NATURAL NUMBERS ?     Of course, all said above is only first steps towards the investigation of the Cognitive Reality World of Virtual Geometrical Objects, being generated by the common Natural Numbers. We have a lot of absolutely new, fantastical results in that area [1-10], and an experience which shows that all this is needed very much especially for modern children.
Therefore, we have some real projects as to "Education via hot CCG-Discoveries". But our computer, financial supporting, etc. is very limited by virtue of well known Russian reasons.
    So, any help and collaboration are wellcome.
    Send any suggestions and comments to alexzen@com2com.ru

REFERENCES:

1. A.A.Zenkin, Cognitive Computer Graphics. Applications in Number Theory. - Moscow: "NAUKA", PhysMath. Literature, 1991, 191 pp.; 30 000 copies.
2. The WEB-Site http://www.com2com.ru/alexzen/
3. A. A.Zenkin, Cognitive (Semantic) Visualization of the Continuum Problem and Mirror-Symmetric Proofs in the Transfinite Number Theory. - International e-journal "VISUAL MATHEMATICS", Vol. 2, at the WEB-Sites:
http://www.mi.sanu.ac.yu/vismath/zen/index.html
http://members.tripod.com/vismath1/zen/index.html
4. A.A.Zenkin, Waring's problem from the standpoint of the cognitive interactive computer graphics. - An International Journal - "Mathematical and Computer Modelling", Vol.13, No. 11, pp. 9 - 25, 1990.
5. A.A.Zenkin, Some picturesque generalizations of Nechaev-Waring's problem obtained by means of cognitive interactive computer graphics. - An International Journal "Mathematical and Computer Modelling", Vol.13, No. 11, pp. 27 - 36, 1990.
6 A.A.Zenkin, Generalized Waring's Problem: On One New Additive Property of Natural Numbers. - “Matem. Zametki”, Том 58, No.3, 372 - 378, 1995 {Translated in: "Mathematical Notes", vol. 58, no. 3, pp.933-937 (1995)}.
7. A.A.Zenkin, Superinduction: A New Method For Proving General Mathematical Statements With A Computer. - Doklady Mathematics, Vol.55, No.3, pp. 410-413 (1997). Translated from Doklady Alademii Nauk, Vol 354, No. 5, 1997, pp. 587 - 589.
8. A.A.Zenkin, The Time-Sharing Principle and Analysis of One Class of Quasi-Finite Reliable Reasonings (with G.Cantor's Theorem on the Uncountability as an Example) - Doklady Mathematics, vol 56, No. 2, pp. 763-765 (1997). Translated from Doklady Akademii Nauk, Vol 356, No. 6, pp. 733 - 735.(1997).

############################################

Prof. Alexander A. Zenkin,
Doctor of Physical and Mathematical Sciences,
Leading Research Scientist of the Computing Center
of the Russian Academy of Sciences,
Member of the AI-Association and the Philosophical Society of the Russia,
Full-Member of the Creative Union of the Russia Painters.
e-mail: alexzen@com2com.ru
WEB-Site http://www.com2com.ru/alexzen
"Artistic "PI"-Number Gallery":
http://www.com2com.ru/alexzen/gallery/Gallery.html

############################################

"Infinitum Actu Non Datur" - Aristotle.
"Drawing is a very useful tool against the uncertainty of words" - Leibniz.

n=4
l	-4	-3	-2	-1	0	1	2	3	4
8n+l	28	29	30	31	32	33	34	35	36
Theory	784	841	900	961	1024	1089	1156	1225	1296
Experiment	784	841	900	961	1024	1089	1156	1225	1296

	BASIC MATHEMATICAL OBJECT	GENERATING NUMBER-THEORETICAL SET	NEW VIRTUAL GEOMETIRCAL OBJECTS
1	The Series of Natural Numbers (I)	The set of squares of natural numbers (II): {1,4,9,16,25, . . .}	Parabolic solitons, running along the series (I)
2	The Series of Natural Numbers (I)	The set of (generalized) Fibonacci's Numbers (IV)	Virtual Fibonacci's Triangles jumping along the series (I)
3	The Series of Natural Numbers (I)	? ? ?	? ? ?
. . .	. . .	. . .	. . .