НОВЫЙ ПОДХОД К АНАЛИЗУ ПРОБЛЕМЫ ПАРАДОКСОВ
(Опубликовано в журнале "Вопросы философии", 2000,
№10, стр. 79-90)
А.А.ЗЕНКИН
(Вычислительный Центр РАН; e-mail: alexzen@com2com.ru )
1. История вопроса.
Знаменитое высказывание "Критяне всегда лжецы" приводится Апостолом Павлом (Библия, Новый Завет, "Послание к Титу", I.12) как принадлежащее одному критскому "стихотворцу", которого раннее христианство отождествляло с Эпименидом (VI век до н.э.). В форме, очищенной от субъективных эмоций и произвольных домыслов, этот парадокс Эпименида звучит так: "Я - лжец!" - "Лжец ли я?"
ЕСЛИ я - лжец, ТО я лгу, когда утверждаю, что я - лжец, и, следовательно, я - не лжец. Но
ЕСЛИ я - не лжец, ТО я говорю правду, когда утверждаю, что я - лжец, и, следовательно, я - лжец.
Обозначая утверждение "я - лжец" буквой А, а отрицание этого утверждения через Ш А, мы можем переписать это "рассуждение" в краткой символической форме:
(A ® Ш A) & (Ш A ® A). (1)
Очевидно, что из (1) и формально, и содержательно следует неразрешимое противоречие:
A & Ш A, (2)
т.е. я - лжец и не лжец "в одно и то же время, в одном и том же месте, в одном и том же отношении".
Более 2500 лет человечество безуспешно пытается разрешить это противоречие, возникающее, казалось бы, на самом элементарном (т.е. фундаментальном) уровне классической логики Аристотеля. Однако, последнее, т.е. существование неразрешимого противоречия (2) в "рамках" классической логики, никогда не служило поводом для того, чтобы усомниться в непротиворечивости самой этой логики. Более того, вся наука (в том числе, - и современная) всегда строилась именно на логике Аристотеля, и вся тысячелетняя практическая деятельность человечества, основанная на этой науке и на этой логике, убеждает нас в том, что противоречие (2), по-видимому, не имеет никакого отношения к логике Аристотеля.
Совсем иная ситуация сложилась в математике, когда в начале ХХ века Б.Рассел открыл свои знаменитые парадоксы, - семантические и чисто формальные аналоги "Лжеца", - которые потрясли самые ее основы и ознаменовали собой начало знаменитого Третьего Великого Кризиса оснований математики. Реакция многих выдающихся математиков на этот Кризис напоминала последние минуты гибели "Титаника". Было предложено несколько радикальных "технологий" преодоления Кризиса, рожденных искренним желанием избавить математику от парадоксов и противоречий (см. [1]).
__________
Рассел, например, считал, что корнем всех "парадоксальных зол" является так называемая "самоприменимость" понятий и потому предложил запретить использование в математике таких логических конструкций, в которых нечто утверждается или отрицается относительно самих этих конструкций (логицизм).
Брауэр отказался от использования закона исключенного третьего (интуиционизм), что, по образному, но очень точному выражению Гильберта равносильно тому, как если бы "боксерам запретили пользоваться на ринге кулаками".
Сам же Гильберт вообще предложил изгнать семантику-смысл из математических утверждений (формализм) и свести всю математику к "игре в символы" (мета-математика, претендующая на то, чтобы стать "единственно верной" теорией доказательства, и рассматривающая всю математику от Пифагора до наших дней как содержательную, неформальную, т.е. "наивную", и потому не отвечающую мета-математическим критериям строгости доказательств.).
Общим для всех этих "технологий", более похожих на грубое хирургической вмешательство, чем (по мягкому выражению Гильберта) на "лекарства против парадоксов", является готовность пожертвовать любой частью здорового тела математической науки, но не столько для избавления математики от парадоксов (см. ниже), сколько ради сохранения … теории трансфинитных чисел Г.Кантора, которая, например тому же Гильберту представлялась "заслуживающим удивления цветком математического духа и вообще одним из высших достижений чисто умственной деятельности человека" (см. [2]). Хотя ни для кого и никогда не было секретом, что для "спасения" математического "Титаника" было достаточно "запретить" использование в математике актуальной бесконечности и "пожертвовать" именно теорией трансфинитных чисел Георга Кантора. Однако, никто из указанных (и неуказанных) выше борцов за дело, которое "выходит за пределы узких интересов специальных наук" (см. [1]), не пожелал "покинуть рай, в который привел математиков Кантор, и удалиться в менее роскошные, но более надежные обиталища" (см. [2]). Относительно надежности логических оснований канторовского "рая" см. статью автора "Ошибка Георга Кантора" в [4].
Но, как известно, не бывает правил без исключений, и в этом смысле, пожалуй, дальновиднее всех поступил Г.Вейль, который, по его собственному признанию все же решил удалиться в далекие от всяких парадоксов, более спокойные и надежные области математики (см. [3]). Примечательно, что примеру Вейля последовали 99% работающих математиков, т.е. таких математиков, чьи научные результаты, в конечном счете, являются доступными верификации "числом или экспериментом". Многие из них просто не пожелали воспринять проблему парадоксов как имеющую отношение к математической науке (ср. отношение большинства логиков к парадоксу "Лжеца"), а один известный современный математик озвучил такую "политику активного невмешательства" таким образом, что математика по природе своей развивается чисто поступательно, постоянно и неуклонно "прирастая" доказательствами новых теорем, и не знает никаких потрясений и кризисов, столь характерных, скажем, для физики начала ХХ века.
Сегодня можно констатировать, что услилия Рассела, Брауэра, Гильберта и вообще всей мета-математики ХХ века были направлены на то, чтобы обойти проблему парадоксов, а не на то, чтобы решить эту проблему. Причем, в соответствии с традицией классической логики и классической математики, под решением проблемы парадоксов мы понимаем явную формулировку необходимых и достаточных условий самого феномена парадоксальности. К сожалению, до сих пор этого не было сделано.
Как бы то ни было, но нельзя остаться равнодушным к поистине выстраданному воплю великой математической души: "… состояние, в котором мы находимся сейчас в отношении парадоксов, на продолжительное время невыносимо. Подумайте: в математике - этом образце достоверности и истинности, - образование понятий и ход умозаключений, как их всякий изучает, преподает и применяет, приводят к нелепостям. Где же искать надежность и истинность, если даже само математическое мышление дает осечку?" (см. [2]). Это признание Гильберт сделал в 1925 году.
Однако, спустя и два десятилетия это "невыносимое состояние" остается неизменным: "Мы меньше, чем когда-либо, уверены в первичных основах (логики и) математики. Как все и вся в мире сегодня, мы переживаем “кризис”.(Г.Вейль, 1946 г., см. [3])
А еще через десять лет "трагические краски" сгущаются: "Не существует, да и не предвидится, никакого единого и общепринятого способа перестройки математики, и в этом смысле кризис оснований … продолжается" (см. [3]).
Увы, и сегодня, сто лет спустя, на пороге третьего тысячелетия, решение проблемы парадоксов является столь же вожделенно недосягаемым для мощнейшего аппарата современной математической логики и мета-математики, как и в начале ХХ века.
В такой безысходной ситуации уместно, однако, вспомнить одного из мудрейших математиков, - я имею в виду Гаусса, - который не только был одним из создателей абсолютно непротиворечивой классической теории чисел и потому категорическим противником введения в математику самого понятия актуальной бесконечности, но и настоятельно советовал при решении научных проблем никогда не путать "очевидное невероятное с абсолютно невозможным".
Тем более, что современные информационные технологии предоставляют нам такие возможности решения старых проблем, о которых не могли даже догадываться создатели современной мета-математики и математической логики.
2. Новая классификация парадоксов логики и математики.
Как известно, любая наука начинается с классификации
ее объектов. Поскольку традиционная мета-математическая классификация парадоксов
логики и математики, предложенная Рамсеем (1926 г.), всегда вызывала законное
чувство глубокого неудовлетворения даже у математических логиков (см. примечания
Есенина-Вольпина в [3], стр. 16), мы провели новую классификацию, основанную
на использовании методов классификации, распознавания образов и прогнозирования
поведения сложных систем.
В наших работах (см. [5,6]) описан метод автоматической
классификации произвольного множества объектов. В рамках этого метода объекты
представляются некоторым фиксированным набором произвольных (как дискретных,
так и непрерывных) признаков, а сама задача классификации формулируется как
задача дискретного оптимального управления, в которой максимизируется интегральное
расстояние между классами объектов и одновременно минимизируется количество
переотнесений между ними при повторных итерациях. На базе этого алгоритма была
разработана интерактивная система КЛАРАП
(КЛАссификация
+ РАспознавание
+ Прогнозирование),
которая помимо построения оптимальной классификации заданного множества объектов,
автоматически устраняет несущественные признаки, взвешивает оставшиеся и формирует
понятие о каждом классе как о минимальном подмножестве признаков, наиболее
существенных для данного класса объектов.
Анализ первых результатов автоматической классификации
традиционных парадоксов логики и математики (см. [1,3]), выполненной еще в 1980
г. с помощью системы КЛАРАП на ЭВМ БЭСМ-6 ВЦ РАН, показал, что в широком диапазоне
варьирования параметров управления парадокс "Лжеца" в его сильной, по Клини
(см. [1]), формулировке ("Я - лжец" или "Данное высказывание - ложно") и парадоксы
Рассела, описываемые той же формальной схемой (1), относятся к разным классам,
как и в классификации Рамсея. Подобная семантическая неадекватность классификации
послужила своеобразной подсказкой для учета той универсальной особенности
нашего естественного языка, которая состоит в замене отрицательных понятий
их положительными эквивалентами (например, "НЕ-большой" - "маленький",
"НЕ-умный" - "глупый", "НЕ-истинный" -"ложный" и т.д.). Поэтому мы заменили
традиционные формулировки парадокса "Лжеца" на следующие семантически эквивалентные
формулировки: "Данное высказывание - НЕ-истинно" и "Я - НЕ-правдист". Аналогичной
переформулировке были подвергнуты парадоксы "Импредикабельность", "Гетерологический"
и др. В результате последующей автоматической классификации с помощью системы
КЛАРАП были получены два устойчивых класса К1
и К2.
1. В класс К1
попали парадоксы, которые (см. [7,8,9]) были названы классическими, или
истинными, или изоморфными с точки зрения схемы (1) парадоксами: парадокс
"Лжеца", все парадоксы Рассела, парадокс Греллинга и некоторые другие. Логика
рассуждений, лежащих в основе всех таких парадоксов, описывается схемой (1).
Понятие о классе К1,
автоматически
сформированное системой КЛАРАП, содержит два существенных признака: самоприменимость
и наличие явного отрицания.
Это позволило высказать гипотезу о том, что не самоприменимость как таковая
(Рассел, см. выше), а самоприменимость ("СЯ") с отрицанием ("НЕ"),
- далее, для краткости, конструкция "НЕ+СЯ",
- является истинной причиной появления классических парадоксов.

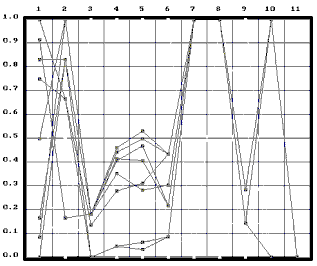
Рис. 1. Визуальный образ класса K1 в системе VISAD. Каждый объект описывается 11 признаками, нормированными на единицу, и изображается ломаной в системе параллельных координат. На экране компьютера каждый объект выделяется индивидуальным цветом. Признаки 7 ("НЕ") и 8 ("СЯ") являются общими для всех парадоксов класса K1.
На рис.1, полученном с помощью системы VISAD
(Interactive CCG-System for VISual
Analysis of Data
- современная версия системы КЛАРАП) (см. [6]), представлены элементы класса
К1,
и можно видеть, что, действительно, только признаки 7 ("НЕ") и 8 ("СЯ") являются
общими для всех парадоксов этого класса.
2. В класс К2
попали парадоксы Кантора, Бурали-Форти, Ришара и ряд квази-парадоксальных рассуждений,
т.е. рассуждения, которые, по нашему мнению, представляют собой явные противоречия
вида (2), причем в этом случае форма (1) не выводима из формы (2) ни формально,
ни содержательно. Существенными признаками понятия о классе К2
являются самоприменимость, и наличие явного противоречия
вида (2), как правило, в форме двух определений одного и того же объекта,
из которых одно отрицает то, что приписывает этому объекту другое определение.
Это свидетельствует о том, что классические парадоксы класса К1,
с одной стороны, и парадоксы типа парадоксов Кантора, Бурали-Форти и Ришара,
с другой, имеют совершенно различную логическую природу.
Сформулируем теперь основной результат, который
является прямым следствием приведенной выше автоматической классификации парадоксов.
(Заметим, что впервые этот результат был доложен 16 марта 1983 г. на заседании
Общемосковского Семинара "Проблемы искусственного интеллекта" в докладе автора
"Применение ЭВМ для исследования проблемы логических парадоксов")
ТЕОРЕМА 1. Самоприменимость с отрицанием, т.е. логическая конструкция "НЕ+СЯ", является необходимым, но недостаточным условием (классической) парадоксальности.
ДОКАЗАТЕЛЬСТВО. Необходимость этих двух условий очевидна: устранение любого из них в формулировке любого истинного парадокса превращает последний в непротиворечивое утверждение. Недостаточность этих двух условий доказывается с помощью тривиального контр-примера: "Брадобрей должен брить всех тех, и только тех, жителей своей деревни, которые НЕ умываютСЯ по четвергам". Очевидно, что в этом утверждении почти расселовского типа есть конструкция "НЕ+СЯ", но нет никакого парадокса.
Итак, если бы Рассел своевременно обратил внимание именно на отрицательный характер самоприменимости в парадоксальных рассуждениях, то математика, вообще, и мета-математика, в частности, возможно, "пошли бы совсем другим путем". Однако, гипнотизирующее, чисто психологическое воздействие позитивной формы предиката "быть лжецом" оказалось столь трудно непреодолимым, что в течение длительного времени и после Рассела семантическая и формальная эквивалентность парадокса "Лжеца" и расселовских парадоксов с явно отрицательной самоприменимостью ("брить тех и только тех, кто НЕ бреет сам СЕБЯ", "множество всех множеств, которые НЕ являются элементами самих СЕБЯ", и т.д.) так и не была эксплицирована.
3. Физическая модель достаточных условий парадоксальности
Для решения вопроса о достаточных условиях парадоксальности мы построили новый парадокс классического типа, - относящийся к области физики, - с помощью которого удалось сформулировать необходимые и достаточные условия его парадоксальности. Затем в рамках этого нового физического парадокса была построена изоморфная модель парадокса "Лжеца", что позволило выяснить достаточные условия и логический механизм парадоксальности последнего - этого прародителя и наиболее характерного представителя всех классических парадоксов логики и математики.
Поскольку самоприменимость понятия естественно рассматривать как операцию его воздействия на самого себя, то конструкцию "НЕ+СЯ" можно интерпретировать как отрицательную обратную связь (см. [11]). Простейшей реальной физической системой с отрицательной обратной связью является инвертор с обратной связью обыкновенной аналоговой вычислительной машины (АВМ) или, что то же, сумматор с двумя входами, из которых один является входом цепи обратной связи (рис. 2). В конце 70-х годов автор был заведующим практикумом по математическому моделированию технологических процессов на АВМ, поэтому на создание такой "физической системы" потребовалось не более трех минут: после подачи на вход сумматора S напряжения X=+100 вольт, стрелка вольтметра W в течение 1-2 секунд плавно (время переходного процесса) переместилась из положения Y=0 в положение Y= - 50 вольт и застыла в этом стационарном положении в полном соответствии с законом аналогового суммирования напряжений Y= - (X+Y), откуда Y= -1/2X. Таким образом, мы получили реальную физическую (и, следовательно, непротиворечивую) модель Мф логической конструкции "НЕ+СЯ".
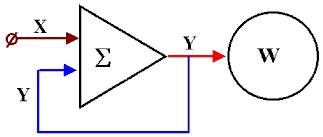
Рис. 2. Программирование на АВМ: стандартная схема инвертора с обратной связью, являющегося физической моделью логической конструкции "НЕ + СЯ".
Как известно, физический сигнал (в нашем случае - электрический ток) распространяется с конечной скоростью V < 300000 км/сек. Что произойдет, если принять V = Ґ ? Первое и самое главное следствие такого предположения заключается в том, что при этом мы, очевидно, выходим за рамки физики! Все остальное является очевидным следствием этого факта: в частности, нефизическими, т.е. нематериальными, виртуальными, становятся сам сигнал, сумматор, вольтметр и т.п. А потому наш нефизический сигнал X=+100 вольт, - без потерь, без сопротивления и без всяких задержек, - мгновенно "проскакивает" через инвертор S и превращается в выходной сигнал Y= -100 вольт, который по цепи обратной связи вновь подается на вход S , складывается с входным сигналом X=+100 вольт, дает на выходе S сигнал Y=0 вольт, который по цепи обратной связи подается на вход S и суммируется с X=+100 вольт, дает на выходе сигнал Y= -100 вольт, и т. д. Другими словами, при ответе на вопрос, какое "напряжение" показывает (виртуальный) вольтметр W на рис. 2, мы получаем следующее довольно странное, потенциально-бесконечное "рассуждение":
(-100 ® 0) & (0 ® -100) & (-100 ® 0) & (0 ® -100) & (-100 ® 0) & . . . ( 3 )
Если заменить входной (произвольный) сигнал X=+100 вольт, например, на X= -1 вольт, то парадоксальная "фраза" (3) обретает более унифицированную "формулировку":
(1 ® 0) & (0 ® 1) & (1 ® 0) & (0 ® 1) & (1 ® 0) & . . . , ( 3а )
Очевидно, что если от этой потенциально-бесконечной "формулировки" отрезать, например, два первых конъюнкта, то мы получаем обычный парадокс в его канонической формулировке (1)
(1 ® 0) & (0 ® 1), ( 3b )
где под 1 и 0 можно понимать, в частности, "да" и "нет", "истину" и "ложь", "брить" и "не брить" себя, "быть" и "не быть" своим собственным элементом и т.д.
Конечно, профессионально искушенный поклонник абсолютной строгости логико-математических рассуждений может задать очевидный вопрос, почему от базовой потенциально-бесконечной "формулировки" (3а) парадоксальной ситуации (3) мы "отрезали" именно два конъюнкта, а не, скажем, три, пять, сто и т.д.? - Возможен только один ответ: "Исключительно потому, что нам так захотелось", - поскольку никаких доводов логического или математикого характера в пользу именно такой двухчленной вивисекции ряда (3а) просто не существует.
Как бы то ни было, но прямым "моделированием" на АВМ доказана следующая
ТЕОРЕМА 2. Достаточным условием превращения реальной физической модели Мф логической конструкции "НЕ+СЯ" в парадоксальную нефизическую модель Мп, является условие V = Ґ , т.е. выход некоторого параметра V (скорости) реального физического сигнала X (элетрического тока) ЗА ГРАНИЦЫ ФИЗИКИ .
Заметим, что такую парадоксальную модель Мп в форме (3а) можно рассматривать как идеальный (виртуальный) переключатель (с бесконечной частотой) величины и знака уже ставшего нефизическим выходного сигнала (напряжения) Y.
4. Достаточное условие логической парадоксальности.
Рассмотрим теперь логическую интерпретацию Мл физической модели Мф. (см. [13]).
1. Физические сигналы X и Y модели Мф
мы будем интерпретировать как обычные логические высказывания (суждения, утверждения
и т.п.) вида "S есть P".
2. Сумматор Sф
интерпретируется как блок Sл
логического доказательства входного логического сигнала Х. Как известно, в
рамках классической логики, процесс доказательства истинности или ложности утверждения
Х представляет собой конечную (!) последовательность высказываний (утверждений,
формул, и т.п.) вида:
Z1, Z2, Z3, …, Zn, (4)
где Z1є
X, и для любого i, 2 Ј i Ј
n, высказывание Zi
либо является аксиомой, либо доказанным ранее утверждением, либо логически следует
из предыдущих высказываний Z1,Z2,
Z3,
…, Zi-1,
по правилам вывода классической логики, а последнее высказывание Zn
є Y является доказанным,
достоверным высказыванием вида "S есть P" (или "S не есть P"), причем
субъект S и предикат P утверждения Y совпадают с субъектом S и предикатом P
исходного (недостоверного, недоказанного) утверждения Х (иначе имеет место тривиальная,
но весьма распространенная и коварная ошибка доказательства - подмена понятий).
Другими словами, входной
логический сигнал Х блока Sл
логического доказательства является гипотетическим, т.е. недостоверным,
утверждением (или обыкновенной гипотезой),
а выходной логический сигнал Y блока Sл
представляет собой доказанное, т.е. достоверное, утверждение.
3. Воздействие физического сигнала обратной
связи Y на входной сигнал X, т.е. операцию сложения двух напряжений X
и Y, естественно интерпретировать как операцию присвоения достоверного
значения логического сигнала Y обратной связи блока Sл
входному логическому сигналу X, т.е. присвоение достоверного значения "есть/не
есть" связки утверждения Y связке входного логического сигнала
X (поскольку субъекты и предикаты этих утверждений - всегда одинаковы).
4. Скорость V прохождения физического сигнала
(электрического тока) X через сумматор Sф
мы будем интерпретировать следующим образом. Естественно предположить, что скорость
любого логического доказательства входного утверждения X будет обратно
пропорциональна длине n этого доказательства. Действительно, чем
больше n в последовательности (4), тем даже чисто формально требуется больше
времени для доказательства гипотезы X, т.е. тем меньше скорость самого доказательства.
Поэтому, естественно постулировать, что скорость логического доказательства
входного логического сигнала X есть V = 1/n.
5. Необходимое
условие парадоксальности физической
модели Мф
"Отрицательная ("НЕ") обратная
связь ("СЯ")" естественным образом трансформируется
в необходимое условие парадоксальности логической
модели Мл
: отрицательная ("НЕ") самоприменимость
("СЯ").
6. Достаточное
условие парадоксальности физической
модели Мф
как ВЫХОД ЗА ГРАНИЦЫ ФИЗИКИ при V
= Ґ
также естественным образом трансформируется в следующее достаточное условие
парадоксальности логической модели Мл
: ВЫХОД ЗА ГРАНИЦЫ ЛОГИКИ
в силу условия n = 0, т.е. V
= Ґ
.
Заметим, что при построении данной логической
модели Мл
мы в явном виде используем, к сожалению, малоизвестную в мета-математике идею
Д.А.Бочвара о внешних и внутренних формах высказываний (см.[12]): для любого
высказывания X = "S e
P" (здесь S - субъект, P - предикат и e
- связка со значениями "есть" или "не есть") высказывания X=И и X=Л (здесь и
далее, И обозначает "истину", Л - "ложь") являются его внешними, а высказывания
"S есть P" и "S не есть P" - внутренними формами.
При этом, довольно неожиданным оказался тот
факт, что указанным, чисто логическим свойствам сигналов модели Мл
соответствуют естественные свойства физических сигналов в модели МФ
: действительно, внешней формой физического сигнала X является его напряжение,
фиксируемое вольтметрам W, а внутренней формой - реальные потоки реально взаимодействующих
электронов (собственно, электрический ток) в сумматоре S
обычной АВМ.
Итак, если теперь на вход логического "сумматора"
Sл
подается любое непарадоксальное (хотя, возможно,
и самоприменимое) высказывание X, то в блоке логического доказательства Sл
внешняя форма, скажем, X=И задает (определяет) конкретное значение связки e
, скажем, "есть" внутренней формы "S есть P" высказывания X и далее реализуется
процесс традиционного доказательства (или опровержения) утверждения "S есть
P" в форме (4). На выходе мы получаем доказанное, достоверное
высказывание Y, внутренней формой которого является уже достоверное высказывание
"S есть P", а внешней - Y=И (соответственно, "S не есть P" - в случае опровержения).
Затем Y подается по цепи обратной связи на вход блока логического доказательства
S Л
и достоверные значения его внешней и внутренней
форм присваиваются соответствующим формам входного сигнала X. Далее, логический
сигнал X может циркулировать по этой схеме сколь угодно долго (как и физический
сигнал в реальной АВМ), но наш логический "вольтметр" W будет показывать стационарное
состояние Y=И. Очевидно, что "в норме" блок логического доказательства S
Л
работает как инвертор только в том случае, если мы не угадали (в общем
случае, произвольным образом задаваемую) внешнюю форму недостоверного
входного высказывания X.
Таким образом, наша модель Мл
"в норме" (!) описывает обычную теорию логического доказательства классической
логики, а Мф
является изоморфной физической моделью этой логической теории.
5. Моделирование "ЛЖЕЦА".
Пусть теперь на вход блока логического доказательства Sл подается сигнал X="X есть Л", т.е. парадокс "Лжеца" в его сильной форме. Достаточно древняя традиция приучила нас рассматривать парадокс "Лжеца" как логическое рассуждение, которое проводится по методу Reductio ad Absurdum. В наших работах (см. [4,7-10]) на примере канторовского доказательства теоремы о несчетности показано, что в рассуждениях типа "если А, то не-А" доказывается истинность следствия не-А (а не его достоверная ложность), что исключает саму возможность заключения "от ложности следствия к ложности основания", т.е. исключает возможность применения правила modus tollens. Последнее означает, что здесь нет никакого метода Reductio ad Absurdum. Фактически же в такого рода "рассуждениях" используется весьма экзотическая (и далеко не безукоризненная с точки зрения классической логики) разновидность метода контр-примера, в которой сам контр-пример ( Ш А) выводится (дедуцируется) из той (недостоверной) гипотезы (А), которую он же и должен опровергнуть. Нетрудно видеть, что парадоксальное рассуждение, порождаемое "Лжецом", являет собой некую предельную форму указанной разновидности метода контр-примера: здесь нет не только метода Reductio ad Absurdum, но и вообще какого бы то ни было логического вывода (дедукции) в смысле классической логики, так что в последовательности (4) следует положить n=0 и, следовательно, "скорость" доказательства V = 1/n = Ґ . Другими словами, парадоксальное рассуждение, как и "физический" сигнал с бесконечной скоростью V = Ґ , представляет собой логический, - а точнее, уже ВНЕ-логический, - переключатель истинностных значений входного парадоксального высказывания X.
Проиллюстрируем сказанное с помощью модели
Мл
.
Итак на вход блока логического доказательства
Sл
подается логический сигнал X="X есть Л".
Поскольку выбор внешней формы недостоверного входного высказывания X произволен
(как и выбор знака входного напряжения в модели Мф),
положим X=И. Это значит, что "истинной" является внутренняя форма высказывания
X - "X есть Л", т.е. "доказано", что высказывание X - ложно и, следовательно,
его внешнюю форму X=И нужно заменить на X=Л. В таком случае, на выходе
блока логического доказательства Sл
мы получаем "достоверный" сигнал
Y с внешней формой X=Л и с неизменной (поскольку n=0) внутренней формой
"X есть Л". Этот сигнал Y по цепи обратной связи подается на вход блока Sл
и логически "складывается" с входным сигналом X, т.е. присваивает ему свои "достоверные"
внешнюю X=Л и внутреннюю "X есть Л" формы. Итак, согласно внешней форме X=Л,
ложно, что "X есть Л", следовательно, внешнюю форму X=Л нужно заменить
на X=И, и на выходе блока Sл
мы получаем "достоверный" сигнал Y с внешней формой X=И и с неизменной
внутренней формой "X есть Л". И т.д. Таким образом, на выходе блока логического
доказательства Sл
(и на нашем логическом "вольтметре") мы получаем
парадоксальную потенциально-бесконечную осцилляцию вида:
Y=И ® Y=Л ® Y=И ® Y=Л ® Y=И ® ... (5)
Сказанное выше можно сформулировать следующим образом.
ТЕОРЕМА 3. Достаточным условием превращения логической модели Мл теории доказательства классической логики в парадоксальную ВНЕ-логическую модель Мп является условие n=0 в (4) или V = Ґ , т.е. принципиальная недоказуемость логического сигнала X="X есть Л" и как следствие - ВЫХОД его ЗА ГРАНИЦЫ ЮРИСДИКЦИИ КЛАССИЧЕСКОЙ ЛОГИКИ .
Заметим и подчеркнем, что в данном случае недоказуемость парадоксального высказывания X="X есть Л" понимается не в традиционном мета-математическом (геделевском) смысле одновременной доказумости Х и его отрицания, а в том смысле, что "доказательство" Х содержит принципиально незавершаемый потенциально-бесконечный (нефинитный, по Гильберту) этап (5).
ТЕОРЕМА 4. Парадокс "Лжеца" X="X есть Л" представляет собой уникальный ВНЕ-логический переключатель истинностных значений его внешней формы X=И или X=Л с помощью его же внутренней формы "X есть Л".
Заметим, что в случае физического парадокса (см. выше) мы получили ВНЕ-физический парадоксальный переключатель, "работающий" с бесконечной частотой. Эта аналогия вполне применима и к "Лжецу" в форме (5). Однако, возможна и другая, более наглядная интерпретация: парадоксальный ВНЕ-логический переключатель (5) представляет собой дискретный пошаговый процесс (автомат). В таком случае важна не скорость перехода от n-го шага к (n+1)-му шагу, а тот факт, что, однажды запущенный, процесс (5) будет продолжаться бесконечно долго. Эпименид первый сказал "Я - Лжец", т.е. подал парадоксальный логический сигнал X на вход блока Sл и тем самым запустил процесс (5). С тех пор каждое новое поколение обреченно, но с неизменным изумлением продолжает воспроизводить один и тот же отнюдь не музыкальный рефрен:
… лжец ® не лжец ® лжец ® не лжец ® лжец ® … (5а)
И тот факт, что из потенциальной Бесконечности, предначертанной "процессу" (5а) его собственной парадоксальной природой, первые 2600 лет уже пройдены, является довольно слабым утешением для тех, кто вслед за Георгом Кантором намеревается достичь его (этого процесса) трансфинитного Конца.
6. Содержательный смысл парадоксальности.
Нам осталось ответить на последний вопрос: каким образом, казалось бы, безупречное использование синтаксиса и семантики классической логики порождает парадокс "Лжеца"? - Очевидный визуально-когнитивный ответ на этот вопрос дает рис. 3. Смысл этого когнитивного мультфильма состоит в следующем.
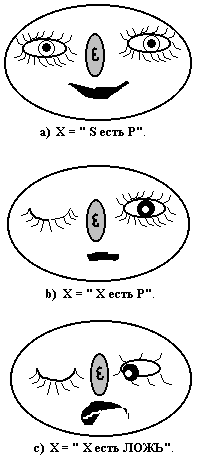
Рис. 3. Визуально-когнитивная модель процесса превращения нормального высказывания (a) в парадоксального логического монстра - "Лжеца" (c).
Как уже говорилось выше, любое утверждение классической логики, в общем случае, имеет вид "S e P" (условные и другие сложно-подчиненные грамматические конструкции высказываний мы здесь не рассматриваем, поскольку они отличаются всего лишь явным включением некоторых фрагментов контекста и не меняют сути дела). Доказательство утверждения "S e P" состоит в том, что мы через содержание субъекта S и предиката P выходим в их контекстное пространство (и в конечном счете - в мир реальных вещей и связей между ними) и строим последовательность (4) с указанными выше свойствами.
Другими словами, субъект S и предикат P любого высказывания являются теми единственными информационными каналами, через которые это высказывание связано (общается) с внешим миром. Очевидно, что такого рода связь утверждения "S e P" с внешним миром через связку e - тривиальна и не представляет для дальнейшего какого-либо специального интереса, ибо все содержание связки e исчерпывается двумя ее значениями "есть" и "не есть".
Как известно, классическая логика не налагает никаких ограничений на субъекты и предикаты высказываний, т.е. все, что угодно, может быть приписано в качестве предиката P любому субъекту S. В этом "произволе" и заключается причина универсальной применимости классической логики в любой области познавательной деятельности человека. С другой стороны, именно это несомненное достоинство свободы конструирования логических утверждений приводит в конечном счете к парадоксам.
Действительно, рассмотрим произвольное высказывание X = "S есть P" (рис. 3a). Если в этом высказывании мы полагаем S=X, то тем самым мы не только получаем самоприменимое высказывание X = "X есть P", но и закрываем S-канал связи этого высказывания с внешним миром (контекстом) через его субъект, поскольку содержание последнего есть само X (рис. 3b). Таким образом содержание субъекта высказывания X исчерпыватся содержанием самого X. Однако, самоприменимость (вопреки Расселу) не является причиной парадоксальности. Действительно, например, самоприменимое высказывание X = "X содержит (есть состоящее из) 100 символов" является ложным и достоверность этой ложности доказывается построением следующей последовательности вида (7) с использованием P-канала связи с внешним (по отношению к высказыванию X) миром:
1) прямым подсчетом убеждаемся (доказываем), что X содержит 37 символов;
2) 37 < 100;
3) Следовательно, X=Л.
Далее, особенность и принципиальное отличие предиката-константы Л от почти всех других предикатов состоит в том, что все его содержание исчерпывается (при наличии указанной самоприменимости) констатирующим утверждением "текущее значение связки высказывания X неверно" и операциональным утверждением "(любое!) текущее значение связки высказывания X следует заменить на противоположное". Короче, если мы полагаем P=Л, то получаем высказывание X = "X есть Л", в котором содержание предиката Л исчерпывается "разговором" о связке высказывания X и, следовательно, P-канал этого высказывания тоже лишает его возможности выхода во внешний мир (рис. 3c). Другими словами, содержание предиката Л (в любых, а не только парадоксальных) высказываниях исчерпывается фиксированным "смотрением" на связку самого этого высказывания.
Таким образом, S- и P-каналы парадоксального высказывания оказываются блокированными, т.е. лишают такое высказывание ВСЕХ связей с внешним миром и самой возможности реализовать (построить) какое бы то ни было доказательство вида (4). Именно последнее обстоятельство, свидетельствующее о принципиальной невозможности построения доказательства вида (4) для парадоксальных высказываний, и является вполне легитимным основанием того, что для таких высказываний в последовательности (4) n=0 и, следовательно, скорость V "доказательства" такого высказывания действительно равна бесконечности.
Таким образом, парадоксальное высказывание X = "X есть Л", т.е. парадокс "Лжеца", представляет собой уникальную квази-логическую реализацию (модель) кантовского ноумена, т.е. "вещи в себе", которая, в данном случае "по построению", не не имеет никаких (в частности, умопостигаемых и логических) связей с миром реальных феноменов.
Вся "механика" превращения легитимного логического объекта во ВНЕ-логическую кантовскую "вещь в себе" и представлена на Рис. 3. Уместно ли такое убогое "одно-косо-глазое" создание, изображенное на рис. 3c, называть высказыванием (суждением, утверждением, формулой и т.д.) и рассматривать его как логический объект - это, конечно, дело вкуса. Впрочем, независимо от этого "вкусового приоритета", синтаксически неизбежное существование парадоксов не может бросить какой-либо негативной тени на семантическую (и формальную) непротиворечивость классической Логики Аристотеля.
Следует заметить, что, по тем же причинам, другой (но уже не противоречивой, а просто пустопорожно-тавтологической) моделью кантовской "вещи в себе" является высказывание X="X есть И".
7. Выводы
1. Истинная природа парадоксов описыватся потенциально-бесконечным, т.е. принципиально незавершаемым, нефинитным в смысле Гильберта, "рассуждением" (5), а не традиционным, произвольно "вырезанным" двухчленным фрагментом (1) этого потенциально-бесконечного "процесса".
2. Достаточное условие парадоксальности, сформулированное выше (Теоремы 3 и 4), доказывает, что парадоксальные рассуждения типа парадокса "Лжеца", являясь синтаксически допустимыми с точки зрения классической Логики Аристотеля конструкциями, тем не менее выходят за рамка этой Логики и представляют собой в очевидном смысле некие квази-логические реализации кантовских ноуменов, т.е. ментальных "сущностей", лишенных каких бы то ни было верифицируемых логических, когнитивных, и т.п. связей с миром реальных феноменологических сущностей. Одним словом, такие парадоксальные рассуждения являются внелогическими конструкциями и могут (точнее, должны) быть удалены из классической Логики Аристотеля как, впрочем, и из математики, без всякого ущерба для последних.
3. В работе [4] показано, что канторовское "доказательство" существования бесконечных множеств, различающихся по их мощности (теорема Г.Кантора о несчетности множества всех действительных чисел), также основано на нефинитном "рассуждении" вида (5). Такое совпадение с результатами настоящей работы, конечно же, не случайно и является достаточно убедительным свидетельством того факта, что исторический "спор" Георга Кантора о природе актуальной бесконечности с Аристотелем, Лейбницем, Беркли, Локком, Гауссом, Коши, Кронекером, Пуанкаре, Бэром, Борелем, Лебегом, Брауэром, Вейлем, Лузиным, Сколемом и др. которые нередко, "… находясь в относительной изоляции, … выказывали полнейшую убежденность в окончательной победе занимаемой ими позиции" [3], завершается в пользу знаменитого не лозунга - пророчества великого Аристотеля: "Infinitum Actu Non Datur", т.е. "нет актуальной бесконечности" потому, что это понятие – внутренне противоречиво и, следовательно, его использование в математике – недопустимо.
ЛИТЕРАТУРА
1. Клини С. Введение
в метаматематику. - М. : Мир, 1957. 526 с.
2. Гильберт Д. Основания Геометрии. - ОГИЗ, Государственное издательство
Технико-Теоретической литературы. - Москва 1948 Ленинград. C. 491
3. Френкель А.А., Бар-Хиллел И. Основания теории множеств. - М. :
Мир, 1966. 553 c.
4. Зенкин А.А. Ошибка Георга Кантора // Вопросы философии, 2000,
No. 2, стр. 165-168;
http://www.com2com.ru/alexzen/papers/vf1/vf-rus.html
.
See also an expanded version “Fatal Mistake of G.Cantor's Theory” (in English)
at
http://www.com2com.ru/alexzen/papers/Cantor/Fatal_Mistake_of_Cantor.html
5. Зенкин А.И., Зенкин А.А.
Об одном методе построения оптимальных классификаций // Discrete Mathematics,
Banach Center Publications. 1982. V. 7. P. 197-204.
6. Зенкин А. А. Когнитивная компьютерная графика. Применения в теории
натуральных чисел. - Москва : "Наука", 1991. C. 190;
http://www.com2com.ru/alexzen/papers.html
7. Зенкин А.А. О Логике Некоторых Квази-Финитных Рассуждений Теории
Множеств и Метаматематики. Новый Парадокс Канторовской Теории Множеств // Новости
искусственного интеллекта. 1997. No. 1. C. 64-98, 156-160.
8. Зенкин А.А. Когнитивная визуализация некоторых трансфинитных объектов
канторовской теории множеств. - В сб. "Бесконечность в математике: философские
и исторические аспекты". - М.: "ЯНУС-К", 1997. С. 77-91, 92-96, 184-189, 221-224.
9. Зенкин А.А. Принцип разделения времени и анализ одного класса
квазифинитных правдоподобных рассуждений (на примере теоремы Г.Кантора о несчетности).
- Доклады РАН, том 356, No. 6, 733-735 (1997).
10. Zenkin A.A. Cognitive (Semantic) Visualization Of The Continuum
Problem And Mirror Symmetric Proofs In The Transfinite Numbers Theory // The
e-journal "VISUAL MATHEMATICS" at the WEB-Sites: http://www.mi.sanu.ac.yu/vismath/zen/index.html
11. Сорос Дж. Советская система: к открытому обществу. - М.:
Издательство политич. литературы, 1991. 223 с.
12. Бочвар Д.А. К вопросу о парадоксах математической логики
и теории множеств // Мат. сб. 1944. Т. 15 (57). С. 369-382.
13. Зенкин A.A.
Автоматическая классификация парадокстов логики и математики. Об одной "физической"
модели парадокса "Лжец" // Новости Искусственного Интеллекта, 1997, no. 3, С.
69-79.
АВТОР: Зенкин Александр Александрович, доктор физ.-мат. наук, ведущий научный сотрудник Вычислительного Центра РАН.
e-mail: alexzen@com2com.ru