dan1-e.htm
Doklady Mathematics, Vol.55, No.3, 1997, pp. 410-413. Translated from Doklady Alademii Nauk, Vol 354, No. 5, 1997, pp. 587 - 589.
========================= MATHEMATICS ==============================
Superinduction: A New Method
for Proving General Mathematical Statements with a Computer.
A.A.Zenkin
(Computer Center of the RAS, e-mail: alexzen@com2com.ru)
Presented by Academician A.T.Fomenko February 7, 1997
Received February 11, 1997
Consider the problem on the representation of natural numbers n ³ 1 by sums of the form
![]() ni ³ m, (1)
ni ³ m, (1)
where m ³ 0, r ³ 2, s ³ 1 - are fixed integers.
If m = 0, this is the Classical Waring Problem (CWP), which was formulated in 1770 for the first time. It was not until 1909 that D.Hilbert obtained his famous number-theoretical result - he gave the complete solution to the CWP in the form of the theorem presented in the left column of the Table 1 [1,2].
In the early 1980s, using methods of Cognitive Comuter Graphics (CCG) methods [3 - 5], I saw (in the direct sense of the word) for the first time and formulated the generalization of the CWP to the case of any m ³ 0 and gave the complete solution to the Generalized Waring Problem (GWP) in the form of the theorem, cited in the right column of the Table 1 [3-7].
Here, for arbitrary values of the parameters m ³ 0, r ³ 2, and s ³ 1, we introduce, by definition, the following two families of sets of natural numbers:
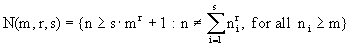 ,
,
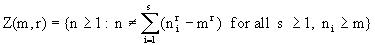 ,
,
and the following two arithmetic functions:
G(m,r) = Arg ![]() { |N(m,r,s)| < ¥ }, g(m,r) = Arg
{ |N(m,r,s)| < ¥ }, g(m,r) = Arg ![]() { |N(m,r,s)| = |Z(m,r)| },
{ |N(m,r,s)| = |Z(m,r)| },
where |X| denotes the number of elements of an arbitrary set X.
Table 1. The Logical Isomorphism of the Classical and Generalized Waring Problems.
|
CLASSICAL WARING'S PROBLEM |
GENERALIZED WARING'S PROBLEM |
|
For the fixed m = 0 and for any r ³ 2 there exists: 1) the minimal number of summands, g(r) º g(0,r), - such that for any s ³ g(0,r): N(0,r,s) = Æ |
For any m = 1, 2, 3, ... and for any r ³ 2 there exist: 1) the minimal number of summands, g(m,r), 2) the finite invariant set, Z(m,r) ¹ Æ , such that for any s ³ g(m,r): N(m,r,s) = {s× mr + z : zÎ Z(m,r)} |
It is easy to see that in the special case m = 0 we obtain the CWP:
G(0,r) º G(r), g(0,r) º g(r), and Z(0,r) = Æ for all r ³ 2.
Thus, for any m³ 0, r³ 2 and s³ g(m,r), the structure of the sets N(m,r,s) is completely determined by the structure of the corresponding sets, Z(m,r), - the so-called invariant sets of GWP.
The pythograms of the invariant sets displayed in the Fig. 1 are read (more precisely, are counted) from left - to right and from top to bottom, (in this case, starting from n=1). If a square is black then the corresponding natural number n Î Z(m,r), and if a square is white, then n Ï Z (m,r).
In [6], the general theorem on the finiteness of the invariant sets Z(m,r) was proved for any m³ 1, r³ 2. However, in practice, it is frequently more convenient to use the constructive finiteness criterion for invariant sets, Z(m,r) that is given by the next theorem [6,8,14].
THEOREM 1. For any m ³ 1 and r ³ 2,
IF $ n*Q(n*), where Q = (i) & (ii) & (iii). and
(i) n* Î Z (m, r);
(ii) n* + i Ï Z(m,r) for each i=1,2,..., k;
(iii) k ³ (m+1)r -mr,
THEN " n> n*P(n), where P(n) = " n Ï Z(m,r) ",
i.e. n * =max {Z(m,r)} and | Z(m, r) | < ¥ .
PROOF. Assume that $ n*Q(n*), but " n > n* P(n) is incorrect. Then there exists a least positive integer, say t ³ 1, such that
1) Ø P(n*+k+t), i.e. n*+k+t Î Z(m,r), and
2) n* + j Ï Z(m,r) for each j = 1, 2, ..., k+t-1, - because t=min,
i.e. if n Î D = [n*+1, n*+k+t-1], then n Ï Z(m,r).
We denote q=(m+1)r-mr, n1=n*+k+t, and n2=n1-q. Then
n2= n1-q=(n*+k+t)-q < n*+k+t-1 - because q > 2 for any m ³ 1, r ³ 2, and
n2= n1-q=n*+(k-q+t) ³ n*+1 - because k-q ³ 0, which follows from the condition (iii) and t ³ 1 according to our assumption. (In what follows, the symbol Þ is read as "follows", for short.)
Thus, n*+1 £ n2 < n*+k+t-1 Þ n2 Î D Þ n2 Ï Z(m,r), - by virtue of (ii).
In such the case, using the definition of Z(m,r), we obtain
n2 = n1 - q = ![]() Þ n1 = q+
Þ n1 = q+ ![]() Þ n1 =
Þ n1 = ![]() Þ
Þ
Þ n1 Ï Z(m,r).
However, the last statement contradicts to the consequence (i) of our assumption. The contradiction obtained proves the theorem. ÿ
Thus, Theorem 1 asserts the validity of the following rather unusual implication: if there exists (at least, one!) a natural number n*, posessing a given set of number-theoretical properties Q(n*), then any n > n* posesses the corresponding number-theoretical property P(n), or - in the more brief symbolic form:
$ n*Q(n*) ® " n>n*P(n). (2)
The extraordinariness of this implication is that its antecedent is a singular statement, but its consequent is a general statement. However, it is obvious, that now to prove the finiteness of invariant sets by means of Theorem 1, it is sufficient to find at the pythogram of the corresponding invariant set Z(1,r) such the element zÎ Z(1,r), - a black square, - which is followed by no less than q(1,r) =2r -1 white squares (naturally, if such a black square exists, since Theorem 1 does not guarantee (!) the existence of such natural numbers). Taking into account, that by m=1
q(1,2) = 3, q(1,3) = 7, q(1,4) = 15,
the pythograms of the invariant sets exhibited in Fig. 1 directly implay that
n*(1,2) = 13, n*(1,3) = 149, n*(1,4) = 2641.
Thus, once having found the numbers n*(1,r) for r=2,3,4, we proved actually the truth of the singular antecedents of implication (2). From this, by modus ponens rule, we immediately infer that " n>n*P(n), - where, by virtue of Theorem 1, P(n) = " n Ï Z(m,r) ", and, hence, the corresponding invariant sets are finite, - What occurs for all n£ n*, can be directly seen in the corresponding pythograms. More strictly, we can see (and, if desired, can even write explicitly) all elements of the corresponding invariant sets Z(1,r), r = 2, 3, 4.
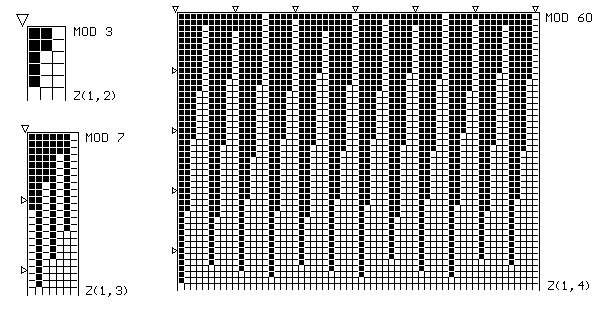
Fig.1. CCG-Images (the so-called pythograms) of the invariant sets of Generalized Waring's Problem, Z(1,r), r=2,3,4. These sets are the new number-theoretical objects that were discovered with the aid of the Cognitive Computer Graphics approach [6].
As is known, classical induction (according to J.S.Mill) is the process of making a plausible inference of a general statement from a particular statement. Therefore, it is quite reasonable to call the process of making a certain inference of a general statement from a singular statement, which is realized in Theorem 1, the method of superinduction.
We present the most general outline of this method [8, 14].
THE METHOD OF SUPERINDUCTION.
1. It is necessary to prove the general statement " n³ 1 P(n).
2. A conditional statemenet
$ n*Q(n*) ® " n>n*P(n), (3)
is constructed (is devised!), where the number-theoretical predicates P and Q = f(P) are distinct, i.e. Q ¹ P.
3. Implication (3) is proved analytically (i.e. a less general statement is deduced from a general one).
4. The truth of the antecedent $ n*Q(n*) of implication (3) is proved; i.e., a natural number n* posessing the number-theoretical property Q is found ( by searching and testing on a computer or even by hand, if you please!).
5. If we succeed in finding such a unique number n*, then the truth of the antecedent $ n*Q(n*) and the truth of the implication $ n* Q(n*) ® " n>n* P(n), which have been proved , implay (by modus ponens) the authentic truth of the consequent, i.e. certain truth of the general statement " n> n* P(n).
6. The truth of the predicate P(n) is checked for all n £ n*:
(a) If " n£ n* P(n), then we have proved " n³ 1 P(n);
(b) Otherwise, we find (explicitely!) all elements of the finite exclusive set, N¨ = { 1£ n£ n* : Ø P (n)}, and thus,
7. We prove the general statement in the form:
" n³ 1 P(n), except for n Î N¨ , where N¨ = { 1£ n£ n* : Ø P(n)}.
In conclusion, we emphasize, that there are no analogues of the method of superinduction in modern mathematics. In particular, this method cannot be reduced to the method of complete mathematical induction, which, as is known, always deals with a unique predicate [13]. The method of superinduction differs essentially from methods based on a direct (analytical!) existence of a threshold element n0 such that $ n0" n>n0 P(n) (see, e.g., the famous solution to CWP for biquadrates [11], which does not contain the implicative part of the form (3) at all), as well as from methods of classical deduction, which infer a less general statement from general one and, as a rule, do without computers. At the same time, construction (at present, invention!) and an analytical proof of implication (3) " from a singular statement to a general one, as well as a computer search for a unique number n*(m,r) followed by computetions (or an inspection of CCG-pythograms in the simplest cases) of the corresponding number-theoretical objects are inherent and unremovable stages of the method of superinduction. Combined together, these stages distinguish the method of superinduction from all known methods of proofs of general mathematical statements of the form " nP(n).
This work was supported by the Russian Foundation for Basic Research (Project no. 96-06-80657) and the Russian Humanitarian Scientific Foundation (Project no. 96-03-04165). I am grateful to Professor V.I.Nechaev for useful discussion of several problems described in this work.
REFERENCES
1. Hua Loo-Keng, Abschatzungen von Exponentialsummen and ihre Anwendung in der Zahlentheorie (The Method of Trigonometric Sums and Its Applications to Number Theory), Leipzig, 1959. Translated under the title Metod trigonometricheskih summ i ego primenenya v teorii chisel, Moscow: Mit, 1964. - M.: MIR, 1964.
2. Hilbert D., Beweis fur die Darstellbarkeit der Ganzen Zahlen durch eine Feste Anzahl n-ter Potenzen, Math. Ann., vol. 67, 281-300 (1909).
3. Zenkin A.A., Generalization of A.Wieferich's Theorem on the Case of Natural Summands. - Doklady AN USSR, 1982, ň.264, No.2, 282-285. {Translated in "Sov. Math. Dokl.", Vol. 25, 616-620 (1982).}
4. Zenkin A.A., Generaliztion of Hilbert-Waring's Theorem. - Vestnik MGU, 1983, Ser. 1, Math., Mech., No. 2, 11-19.
5. Zenkin A.A., Some extensions of Pall's theorem. - Computers and Mathematics with Applications, Vol. 9, 609-615 (1983).
6. Zenkin A.A., Cognitive Computer Graphics - M.: NAUKA, 1991, 192 pp.
7. Zenkin A.A., Waring's problem from the standpoint of the cognitive interactive computer graphics. - Mathematical and Computer Modelling, Vol.13, No. 11, pp. 9 - 25 (1990).
8. Zenkin A.A., Cognitive Computer Graphics: Novelty in Logic of Mathematical Proofs. - XI International Conference on Logic, Methodology and Philosophy of Science, Moscow-Obninsk, Russia, April, 1995. Proceedings, vol.2, pp. 129-136.
9. Zenkin A.A., Waring's problem: g(1,4) = 21 for fourth powers of positive integers.- Computers and Mathematics with Applications, Vol.17, No. 11, pp. 1503 - 1506 (1989).
10.Zenkin A.A., Waring's Problem for sums of biquadrates of positive integers: g(1,4)=21. - Matematicheskie Zametki,vol.54, No.5, 45-56 (1993).
11. Balasubramanian R., Deshouillers J., Dress F., Waring's problem for biquadrates,1:Sketch of the Solution.- Comptes Rendus de l'Academie des Siences, Ser. 1, Math., vol. 303 (4), 85-88 (1986).
12. Pall G., On sums of squares. - Amer. Math. Monthly, 1933, vol.40, 10-18.
13. Polia D., Mathematical Discovery. - M.: NAUKA, 1970. 462 pp.
14. Zenkin A.A., SUPER-INDUCTION METHOD: Logical Acupunctura of Mathematical Infinity. - In the Collection "The Infinity in Mathematics: Philosophical and Hystorical Aspects", Edr. Prof. A.G.Barabashev. - Moscow, "JANUS-K",1997, pp. 152-168, 173-176.
THE AUTHOR: Zenkin Alexander Alexandrovich, Doctor of Phys.-Math. Sciences, Leading Research Scientist of Computing Center of the RAS.
e-mail: alexzen@com2com.ru