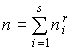 , i = 1,
2, ...., s, (1)
, i = 1,
2, ...., s, (1) Math. Comput. Modelling, Vol.13, No.11, pp.9-25, 1990
WARING'S PROBLEM FROM THE
STANDPOINT
OF THE COGNITIVE INTERACTIVE COMPUTER GRAPHICS
A. A. Zenkin
Moscow State University, Moscow, Russia.
e-mail: alexzen@com2com.ru
(Received December 1988, in reversed form March 1990)
Communicated by Ervin Y. Rodin
Abstract - It is well known that an apt drawing is sometimes capable of generating new ideas in a human mind. The modern Interactive Computer Graphics (ICG) allows the effective use of the cognitive graphics function (in contrast to the more traditional and common illustrative one) even in the most abstract fields of science. A "knowledge-generating" man-mashine ICG-system, DSNT, - the Dialogue System for ICG-investigations in the additive Number Theory, - has been worked out on the basis of the cognitive ICG concept. In the framework of the ICG-system, DSNT, an original method has been worked out for the dynamic visualization of abstract number-theoretic objects in the form of some colour-musical ICG-images or the so-called pythograms of theese objects. Under certain conditions these pythograms can create some new mathematical ideas and hypotheses in an investigator's imagination and provide the ways of their strict proofs.
This paper describes some new results in the well-known field of the abstract number theory - classical Waring's problem. These results have been obtained by means of the cognitive ICG. The author also attempts to describe, or, to put it more precisely, to picture how these results and their proofs are created. The general philosophy of the ICG-visualization of scientific abstractions briefly discussed in the paper can be useful for direct investigations of intuitive creative meta-procedures of our thinking. These investigations will undoubtedly become an important trend in the field of artificial intelligence and computer techniques for self-knowledge and self-education.
1. INTRODUCTION
There are two main functions of Interactive Computer Graphics (ICG): a more traditional and common illustrative function and the so called cognitive one. The illustrative function of ICG allows to picture any real object on the display screen and makes this object recognizable. Whereas the cognitive function enables us (under certain conditions) to depict the intrinsic content, i.e., the essence of the object to be examined even if this object is a complex scientific abstraction. The purposeful utilization of the cognitive function of ICG stimulates our scientific intuition and creative imagination generating new ideas.
In this paper we demonstrate this knowledge-generating possibilities of the cognitive ICG in the field of the so-called classical Waring's problem (CWP) which is a rather abstract, intellectually difficult and well-studied problem. In other words, CWP is the most extreme field of application of any graphics.
E.Lehmer and D.Lehmer [1] were the first who used picturesque possibilities of ICG in the Number Theory. In their pioneer paper the authors put special emphasis on the fact that ICG allowed them first to see and then to prove some new mathematical results. In this paper we use ICG for the same purpose but in a some different way.
2. SOME GENERAL DEFINITIONS
It is known that Waring formulated his famous hypothesis in 1770. It was not until 1909 that D.Hilbert gave a complete solution of CWP. Since then CWP and its numerous generalizations have been the object of particular attention of specialists. To get some new knowlegde in the field of CWP, therefore, is not a simple task. However, it is the cognitive ICG that enables us to look at this classical problem in quite a different way.
Consider the problem of the representation of natural numbers n ³ 1 as sums
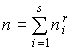 , i = 1,
2, ...., s, (1)
, i = 1,
2, ...., s, (1)
under the following general restriction on the summands
all ni ³ m, (1a)
where m ³ 0, r ³ 2, s ³ 1 are any fixed integral numbers [2].
Further, for any m, r and s we define the following two families of sets of natural numbers:
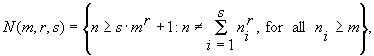
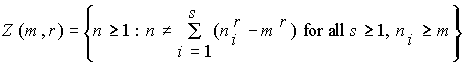
and two arithmetic functions:
![]()
![]()
where | X | denotes the number of elements of the arbitrary set X.
It can be easily seen that if m = 0 then Z(0,r) = Æ , G(0,r) º G(r) and g(0,r) º g(r) for any r ³ 2, where G(r) and g(r) are well-known functions of CWP. In other words, CWP arises if and only if m = 0. If m ³ 1 we deal with the so-called Generalized Waring's Problem (GWP).
The first step from the classical (m = 0) to non-classical case (m = 1) for r = 2 was made by G.Pall, an American mathematician, as early as 1933 [3]. However, to make the next step, which a posteriori seems so obvious, and to generalize the unique result, obtained by Pall, for r=3 appeared to be impossible without the cognitive ICG.
3. VISUALIZATION OF ABSTRACT NUMBER-THEORETIC OBJECTS
Let N denote a series of natural numbers, D = [ n', n" ], denote a fixed segment of the series and P(n), n Î N, denote some number-theoretic predicate given on the set N. Then the two-dimensonal table T = {d ij } consisting of small squares d ij, i = 1,2,..., K, j = 1,2,..., L is an ICG-image of the given segment D . Here K is the number of rows and L is the number of columns in the table T. Figure 1 shows that there exists the following 1-1-correspondence between the set of small squares d ij and the natural numbers nij Î D:
![]()
The number of columns L will be referred to further as a modulus of the given ICG-image, the choice of L being arbitrary.
Let us paint every small square d ij in green, if P(nij) is true, and red, if P(nij) is false (in all the photos presented below white stands for green and black for red). In Fig.1 the predicate P(n) is as follows:
P(n) = "the natural number n can be represented by the sum (1) with m = 0, r = 2, s = 1".
The predicate P(n) corresponds to the simplest case of CWP. However, it is the cognitive ICG that will show this case to have some new, quite unexpected mathematical meaning [3].
In constructing every ICG-image a mathematical music is being produced. The emergence of each small square on the screen is accompanied by some tune which is the musical mark and which varies depending on the colour of the small square and its location in the table T. This enables us not only to see but also to hear some important features of the ICG-images or, more strictly, of the corresponding number-theoretic objects which are responsible for these ICG-images. These features, for example, are some invariants, periodicities and regularities in their structures and so on.
Thus, we can say that the colour of the small squares simulates the additive properties of the corresponding natural numbers nij Î D. Their location simulates the multiplicative properties of natural numbers nij in accordance with the following relation
![]() .
.
On the whole, this ICG-image gives us the possibility to visualize the abstract connection between the abstract properties of additivity and multiplicativity of natural numbers. Moreover, this twofold abstract mathematical connection can be visualized in dynamics by changing the modulus L. It is well-known that this very connection is the basis and the main cause of the overwhelming majority of the classical number theory problems.
If we can visualize this general property of natural numbers, it is not surprising that in the same way we can also see some new number-theoretic facts, ideas and hypotheses.
On the analogy with the well-known REONTGENO-grams of real objects we refer to our colour-musical ICG-images of abstract number-theoretic objects as PUQAGORAS-grams or, shortly, pythograms of these mathematical objects.
We shall see animated cartoons, i.e., the sequencies of the pythograms, demonstrating the life of these abstract mathematical objects. But let us stop the demonstration of any animated cartoon if its last still is repeated infinitely without being changed.
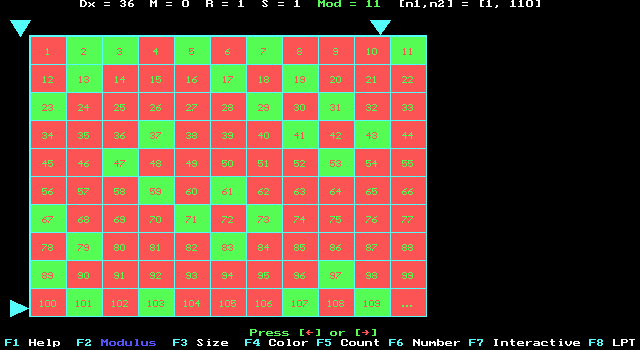
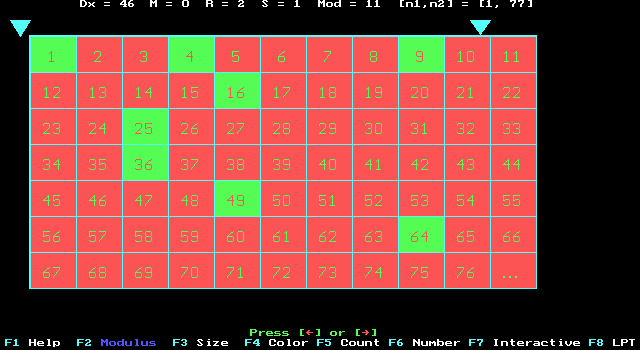
Fig. 2. Pythogram with
the predicate P(n) = “n
is a prime number”
according to the non-optimal modulus, L
= 11.
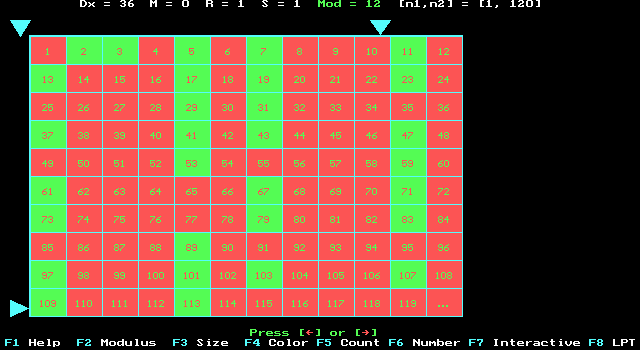
Fig. 3. Pythogram with the same
predicate P(n)= “n is a prime number”,
but according to one of the optimal modulus, L = 12 which
is divisible by 6.
As mentioned above, we can quite arbitrarily change the modulus L of any given pythogram. Obviously, we get different pythograms of the same mathematical object. We call the modulus L an optimal modulus if the picturesque features of the corresponding pythogram may be interpreted mathematically in the simplest way. It should be noted that this definition has, of course, only some heuristical and pragmatical significance.
In Fig.2, for example, the modulus L=11 is not optimal for the pythogram with the predicate
P(n) = “n is a prime number”.
On the other hand, it is clear that the modulus L = 12 in Fig.3 is optimal for the pythogram with the same predicate since this pythogram reveals the follownig well-known property of prime numbers.
ICG-fact 1.
If any natural number n ³ 5 is prime, then it can be written as follows n = 6k ± 1.
All the pythograms presented below are produced by an optimal modulus.
Finally, we oblitarate the natural number nij within the small square because we can always determine it for any given d ij. This enables us to obtain thoughtful and beautiful pythograms (see Fig.4 and Fig.5) of the same mathematical objects. These pythograms have something in common with masterpieces of Malevich and Kandinsky.
4. CLASSICAL WARING'S PROBLEM AS A PICTURESQUE MUSICAL
The classical case corresponds to the following restriction on terms in sums (1):
all ni ³ 0, or m = 0, (1b)
i.e. all ni - are non-negative integers.
We shall follow further the general scheme of ICG-considerations:
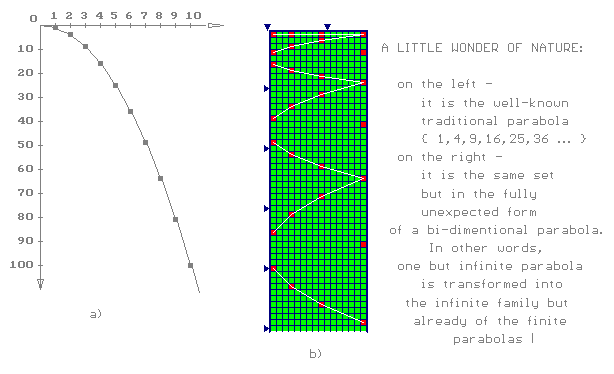
Fig. 4. A little wonder of Nature:
On the left - a well-known traditional graph of the
parabola {1, 4, 9, 16, 25, 36, 49,...};
On the right - the same set {1,4,9,16,25,36,49,...} in a
completely unexpected form of a pythogram according to
the optimal modulus, L= 16. Here the only
but infinite classical parabola, Y = X
2 , X = 1, 2, 3,..., is transformed into the
infinite family of finite parabolas: { X
= (Y/n)2, X = 1,4,9,16}, n
= 1, 2, 3,...
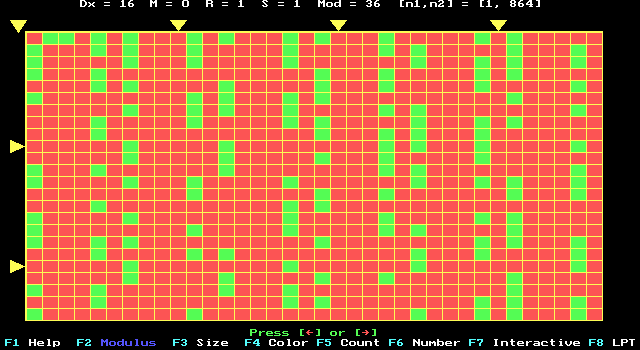
Fig. 5. Picturesque prime numbers according to
one of the optimal modulus L = 36
(L is divisible by 6). Here D = [ 2,
864 ].
Fig. 6. Classical Waring’s problem on sums of squares: g(0,2) = 4. Here D = [1,64].
So we WATCH the animated cartoon (Fig.6) on the set N(0,2,s), s = 1, 2, ...
We SEE
ICG-statement 1. Every still with s ³ 4 is red.
Having expressed this ICG-statement by the traditional mathematical language we get the following famous result:
Lagrange's theorem (1770). g(2) º g(0,2) = 4.
Let us WATCH the animated cartoon (Fig.7) on the sets N(0,3,s), s = 1, 2, ...
We SEE
ICG-statement 2. Every still with s ³ 9 is red.
The translation into the mathematical language gives:
Wieferich's theorem (1909). g(3) º g(0,3) = 9.
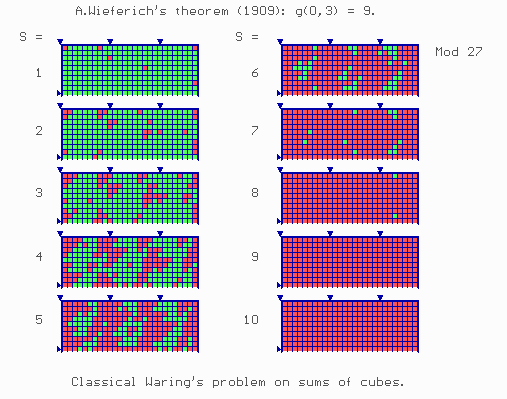
Fig. 7. Classical Waring's problem on sums of
cubes: g(0,3) = 9.
Here if s = 7 we can see famous Linnik's theorem on the sums of
seven cubes:
G(0,3) £ 7. Here D
= [ 1, 270 ].
If we WATCH the animated cartoon on the sets N(0,4,s), s = 1, 2, ... (it being too long we can present it in this paper) then we SEE
ICG-statement 3. Every still with s ³ 19 is red.
Having translated this ICG-statement into mathematical language, we get the following remarkable result:
The theorem of R.Balasubramanian, J.Deshouillers and F.Dress (1986).
All these ICG-statements obtained while watching the corresponding animated cartoons are computer hypotheses and subsequently call for a rigorous mathematical proof.
Therefore, generalizing the above ICG-statements 1, 2 and 3, we obtain the famous number-theoretic statements.
Waring's Hypothesis (1770).
For any r ³ 2 there exists the smallest number of summands in sums (1) which depends on r only and which is designated by g(r) º g(0, r), such that g(0, r) < ¥ for all r.
5. THE FIRST ICG-EXTENSION BEYOND THE CWP
This non-classical case corresponds to the following restriction on summands in sums (1):
all ni ³ 1 or m = 1, (1c)
i.e. all ni - are positive integers.
In the framework of the ICG-system DSNT the transfer to the non-classical case is accomplished by substituting the classical value m = 0 to the non-classical value m = 1. Then we follow the general procedure of our ICG-investigations.
Let us WATCH the animated cartoon (Fig.8) on the sets N(1,2,s), s = 1, 2, ... .
We SEE
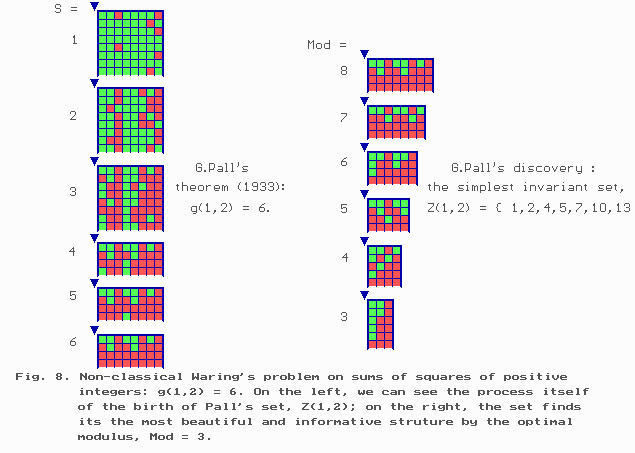
Fig. 8. First approach to the generalization of
classical Waring's problem is Pall's theorem:
g(1,2) = 6. Here the process of creation of the simplest
invariant set Z(1,2) = { 1,2,4,5,7,10,13 },
is present. Here D = [ s+1,n’ ]
where n’ is equal to s+64 for s = 1,2,3 and s+32 for s = 4,5,6.
ICG-statement 4.
g(1,2) = 6, i.e. for any s ³ g(1,2) the set N(1,2,s) is of the form
N(1,2,s) = { s + z : z Î Z(1,2) }
where
Z(1,2) = { 1, 2, 4, 5, 7, 10, 13 }.
It is this ICG-statement which was first formulated and proved by G.Pall [3]. It can be easily seen that Pall's theorem is the generalization of the famous Lagrange's theorem on the squares of positive integers. This theorem was the first step in a new and rather natural generalization of CWP. However, the classical method used by G.Pall for proving his theorem appeared to be inapplicable even when r = 3. Nevertheless, there is no difficulty in generalizing CWP in the framework of the cognitive ICG-system, DSNT.
Let us WATCH the animated cartoon (Fig.9) about the sets N(1,3,s), s = 1, 2, ... .
We SEE
ICG-statement 5.
g(1,3) = 14, i.e. for any s ³ g(1,3) the set N(1,3,s) is of the form
N(1,3,s) = { s + z : z Î Z(1,3) },
where
Z(1,3) = { 1 - 6, 8 - 13, ..., 142, 149; elements not indicated here
can be seen directly in Fig. 9, on the pythogram with s = 14 }.
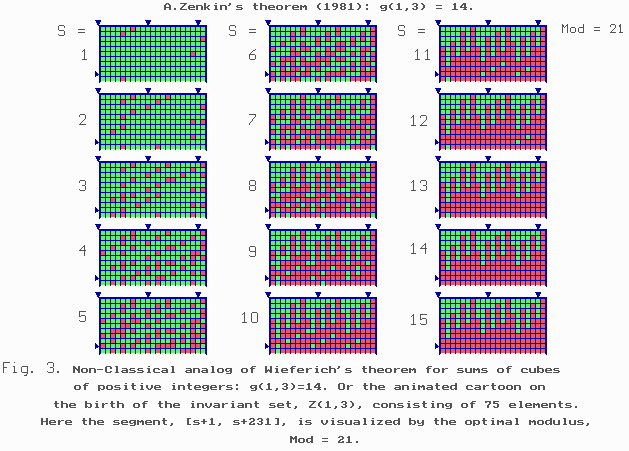
Fig. 9. Animated cartoon on the creation of the
invariant set Z(1,3)
consisting of 75 elements: g(1,3)= 14. Here D
= [s+1, s+231].
Optimal modulus L = 21, i.e., it is divisable by 7.
If we could WATCH now the animated cartoon about the sets N(1,4,s), s = 1, 2, ..., (it is too long to be shown here), we should SEE
ICG-statement 6.
g(1,4) = 21, i.e. for any s ³ g(1,4) the set N(1,3,s)
is of the form
N(1,4,s) = { s + z : z Î Z(1,4) },
where
Z(1,4) = { 1-14,16-29, ..., 2626,2641; elements
which are not shown here can be seen
in Fig. 11, on the pythogram of the so-called invariant
set Z(1,4) }.
Using a much more powerful computer we could SEE the following
ICG-statement 7. g(1,5) = 57.
This ICG-statement was obtained as a computer hypothesis in 1981. To provide its rigorous mathematical proof without using the cognitive ICG will not, however, be an easy task.
The proofs of ICG-statements 4, 5 and 6 will be presented below by means of one general computer method. But even at this point we can formulate the following generalization of Pall's theorem for any r ³ 2.
ICG-statement 8.
For m = 1 and for any r > 2 there exist:
such that for all s > g(1,r)
N(1,r,s) = { s + z : z Î Z(1,r) }.
6. GENERALIZED WARING'S PROBLEM (GWP). THE CASE m ³ 1.
It is well-known that for any m ³ 0, r ³ 2, s ³ 1
| N(m,r,s) | ³ | N(m,r,s+1) |
A more careful review of the animated cartoons shown in Figs. 6-9 yields:
ICG-statement 9. For any m ³ 0, r ³ 2, s ³ 1 | N(m,r,s) | > | N(m,r,s+1) |
The following generalization of Waring's problem for any m ³ 1 was proved using this ICG-statement [5].
Theorem 1.
For any m ³ 0, r ³ 2 there exist:
such that for all s ³ g(m,r)
N(m,r,s) = { s× mr + z : z Î Z(m,r) }.
This theorem is proved with the aid of elementary methods by induction on m. The 0-step of the induction is CWP, or more precisely, the following statement first proved by D.Hilbert.
Hilbert's theorem (1909).
For m = 0 and for all r ³ 2 there exists the smallest number of summands, g(r) º g(0,r), in sums (1) such that for all s ³ g(0,r) N(0,r,s) = Æ .
It is to be reminded that if m = 0 then Z(0,r) = Æ for all r ³ 2.
7. ICG-METHOD OF ESTIMATION OF THE FUNCTIONS G(m,r) AND g(m,r)
It is known that obtaining particular values of functions G(r) º G(0,r) and g(r) º g(0,r) is, even at present, the most important task of CWP. It is quite natural, therefore, that we attempt to provide a general method for estimating G(m,r) and g(m,r) for any values of parameters m ³ 1 and r ³ 2. The essence of the ICG-method is as follows. Let the truth of some general assertion be shown say, " n B(n). We find some particular assertion, say A, such that " n B(n) follows from A. If we can prove analitically the truth of the conditional statement,
A ® " n B(n),
and if the truth of the particular statement A can be proved by a direct visual verification on a computer, then the truth of the general assertion " n B(n) is proved by classical modus ponens rule:
A, A ® " n B(n) ú - " n B(n).
One of these implications which is important for our aims is
given namely in the form of
A ® "
n B(n) by the following theorem.
Theorem 2. For any m ³ 1 and for any r ³ 2,
for all
(2)
s = s0, s0+1, s0+2, ..., s1,
where
s1 - s0 ³ g(m - 1, r), (3)
(4)
i.e.
G(m,r) £ g(m-1,r) + s0, (5)
where
n0(m,r) = n*(m,r) + (g(m-1,r)+s0)× (m-1)r +
, (6)
PROOF . Fix
arbitrarily m ³
1, r ³ 2 and
let the value of g(m-1, r) be known, then by definition
of the function g(m,r), any natural number n
> g(m-1,r)× (m-1)r
+ ![]() is a sum
is a sum
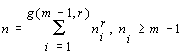 . (7)
. (7)
Let there exists a natural number n*(m,r) with the property (2). Then any natural number
n > ![]() (m, r) = g(m-1,
r)× (m-1)r
+
(m, r) = g(m-1,
r)× (m-1)r
+ ![]() + n*(m,
r), (8)
+ n*(m,
r), (8)
can be represented as a sum n = n*(m,r) + n1,
where n1 > g(m-1, r)× (m-1)r
+ ![]() , and,
therefore,
, and,
therefore,
n1 is representable as a sum (7). Thus,
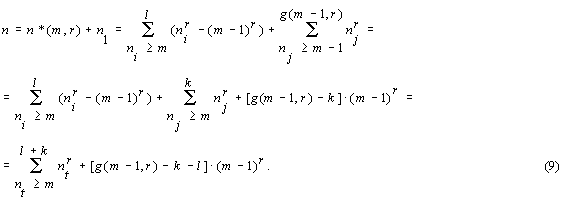
Let
l = g(m-1,r) + s0 - k. (10)
The latter equality is admissible since from (10) and the obvious condition
1 £ k £ g(m-1,r), it follows that s0 < l < g(m-1,r) + s0 - 1 < s1 .
Then in sums (9) we have
l+k = [ g(m-1,r) + s0 - k ] + k = g(m-1,r) + s0 ,
and
{ g(m-1,r) - k - [g(m-1,r) + s0 - k] } = - s0 ,
so that any natural number n > ![]() (m,r)
can be represented as the sum
(m,r)
can be represented as the sum
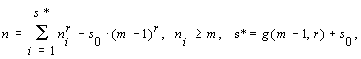
or
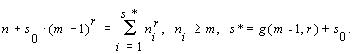
Supposing now
![]() ,
,
we find that any natural number n > n0 (m,r) can be represented as a sum
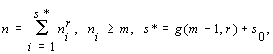
i.e.
G(m,r) £ g(m-1,r) + s0.
We have, thus, proved the theorem. ÿ
Now, to obtain the estimation of G(m,r) we need to know the exact value of g(m-1,r) and the number n*(m,r) with the property (2) if this number exists. To obtain the exact value of g(m,r) it is necessary to look through pythograms of the sets,
N(m,r,s), s = g(m-1,r) + s0 , g(m-1,r) + s0 + 1, ...
in the segment D = [s× mr , n*(m,r) ] until the condition
|N(m,r,s)| = |Z(m,r)|
is the case on the segment D [8, 12, 13]. Some results obtained with the aid of Theorem 2 and the ICG-methodology of the cognitive visualization are summing up in Tables 1 and 2.
Table 1. Generalized Waring’s problem for r-th powers of positive integers, m = 1, r = 2,3,4.
r |
min n*(1,r) |
s0 |
s1 |
results |
2 |
169 |
1 |
=155 |
G(1, 2) = 5 |
g(1, 2) = 6 |
||||
3 |
1 072 |
2 |
>900 |
G(1, 3) £ 9 |
g(1, 3) = 14 |
||||
4 |
77 900 162 |
2 |
> 77 897 000 |
G(1, 4) £ 18 |
g(1, 4) = 21 |
Table 2. Generalized Waring’s problem for sums of squares for different m.
m |
n*(m,2) |
s0 |
s1 |
g(m,2) |
|
0 |
- |
- |
- |
4 |
|
1 |
169 |
1 |
= 155 |
6 |
|
2 |
143 |
1 |
³ 20 |
8 |
|
3 |
117 |
1 |
= 12 |
8 |
|
4 |
247 |
1 |
³ 20 |
8 |
|
5 |
273 |
1 |
= 19 |
8 |
|
6 |
375 |
1 |
= 24 |
10 |
|
7 |
493 |
1 |
= 27 |
9 |
|
8 |
480 |
1 |
= 22 |
11 |
|
9 |
377 |
1 |
= 15 |
12 |
|
10 |
703 |
1 |
= 27 |
10 |
|
8. SOME ESTIMATIONS OF G(m,r) AND g(m,r)
In the framework of the cognitive ICG-system DSNT we found the
smallest natural numbers
n*(1,r ) for r = 2,3,4 (see Table 1).
Then, a simple viewing of pythograms of the corresponding sets,
N(1,r,s), s = g(0,r) + s0, g(0,r) + s0 + 1, g(0,r) + s0 + 2, ...
in the segment D = [ s+1, n’ ], where n’ > n*(1,r), enabled us to prove our ICG-statements 4, 5, 6.
We shall show in more detail how the ICG-method of obtaining estimations of G(m,r) and g(m,r) works if m = 1, r = 2.
In Fig.10 a close-up of Pall's theorem is given for s = 4,5,6. The natural number n*(1,2) = 169 is marked by a small asterisk (in the 21st row).
Let us WATCH the still with s = 4.
We SEE
Decarte's Theorem [3].
Numbers of the form
2 · 4h, 6 · 4h, 14 · 4h, h = 0,1,2,...,
are not representable by sums of four squares of positive integers.
From this theorem we get the following important result:
G(1,2) > 4.
Our theorem 2, on the other hand, gives
G(1,2) £ g(0,2) + s0 = 5,
thus, the following statement takes place.
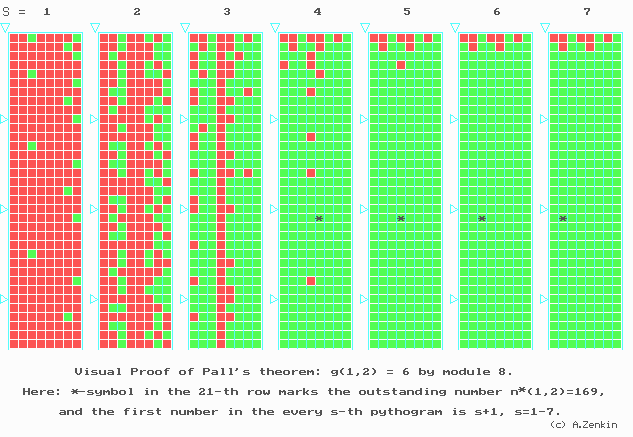
Fig.10. The close-up stills of Pall's theorem
when s = 4,5,6,7.
Here the small asterisk in the 21st row marks the number n*(1,2)
= 169 =
- = 132 =
= 122 + 52 =
= 122 + 42 + 32 =
= 112 + 42 + 42 + 42 =
= 102 + 62 + 42 + 42 + 12 = ...
Here D = [ s+1, s+256 ].
Theorem 3. G(1,2) = 5. (11)
Let us WATCH the still with s = 5.
We SEE the result (11) as follows.
Theorem 4 [3].
Among natural numbers n £ 169 only the numbers 1,2,3,4, 5 + z and 33, where z Î Z(1,2), can not be represented by sums of five squares of positive integers.
The still with s = 6 provides the strict proof of ICG-statement 4.
It should be noted here that the fact of the strict inequality
G(0,2) < G(1,2) (12)
is very important to understand the nature of GWP.
In the same way we can prove our generalization of Pall's theorem in the form of ICG-statement 8 for r = 3 and r = 4. The corresponding invariant sets Z(1,r), r = 2,3,4 are given in Fig. 11.
The ICG-method described above also allowed us to prove all the results concerning the exact values of g(m,r) for m = 1 ¸ 10, r = 2 which were published earlier in [2] as computer hypotheses. The corresponding invariant sets Z(m,2) are presented in Fig.12.
Using the results obtained in [8] we have the general iterative estimation of G(m,r) for any m ³ 1, r ³ 2
G(m,r) £ G*(m,r), (13)
where
G*(m,r) = G*(m-1,r) × [(m+1) r + (m-1) r ] + (m+1) r -m r -1, (14)
and
G*(0,r) = G(0,r) º G(r). (15)

Fig.11. Pythograms of the invariant sets Z(1,r), r = 2,3,4 according to the optimal moduluses.
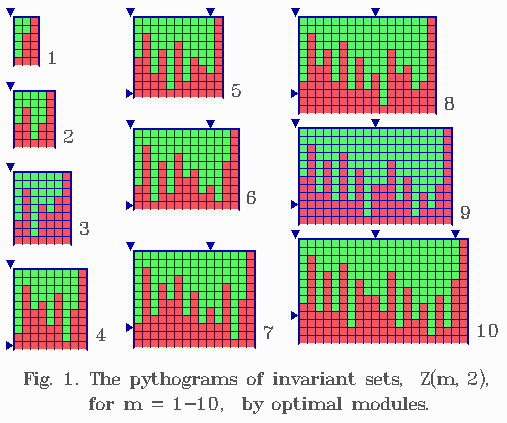
Fig.12. Pythograms of the invariant sets Z(m,2), m = 1 ¸ 10 according to the optimal moduluses.
It is obvious that the accuracy of (13) for m ³ 1 depends essentially on the accuracy of the initial approximation (15) for m = 0. Replacing (15) by the best asymptotic estimation,
G(0,r) = G(r) < r (2 log r + 2 log log r + 12), (16)
obtained by A.Karatzuba [9] in 1985 on the basis of Vinogradov's method, we get for m = 1
G(1,r) < 2 r+1 × r × (log r + loglog r + 6) + 2r - 2, (17)
and then using the iterative formula (14) we get estimates (13) for any m ³ 2. It should be, however, taken into account that Karatsuba's estimate (16) is valid only for r ³ 4000.
Undoubtedly, the estimates of G(m,r) based on the iterative formula (14) can be improved. In this point, however, it is to be noted that these estimates for any m ³ 1 have been obtained for the first time and by elementary methods.
9. SOME COMMON REMARKS CONCERNING GWP.
As it is known [6,7], CWP can be considered as a problem of summing up infinite sequences
{ 0 r , 1r , 2r , ... , (m-1) r , m r , (m + 1) r , ... }. (A)
In terms of Shnirelman's theory of set densities the main result of CWP will have the following form [7,10].
Hilbert's theorem.
For any r ³ 2 the sequence (A) is the basis of the order, g(r) º g(0,r), for the whole series of natural numbers.
In this case our Theorem 1, which gives a complete solution of GWP, can be rewritten in the following way [12].
Theorem 1.
For any m ³ 0, r ³ 2 the sequence of r-th powers of natural numbers
{ m r , (m+1) r , (m+2) r , ...} (B)
is the basis of the finite order, g(m,r), for the whole series of natural numbers except for the numbers 1,2,3, ..., g(m,r) × m r - 1 and those of the form g(m,r) × m r + z, z Î Z(m,r).
Shnirelman's theory is known to be valid only in the case of summing up infinite number sequences of the type (A), i.e. sequences containing zero. This theory is not applicable to the case m ³ 1 [10]. Our Theorem 1 proves that Shnirelman's theory can be generalized to the case of anym ³ 1, i.e. to the case of summing up infinite number sequences (A) without any initial segment.
It is also interesting to extend the well-known result of Loo-Keng Hua [10] on estimations of G-type functions for polynomials with non-classical restrictions m ³ 1 to the domain of polynomials. The nonmonotone increase of g(m,2) when m = 0,1,2, ..., and the strict inequality (12) show that this extension will not be too trivial.
It is also of interest to prove the existence of n*(m,r) for any m ³ 1, r ³ 2 [11-13].
Acknowledgement.- The author is grateful to academician G.S.Pospelov and Profs D.A.Pospelov and V.I.Nechaev for helpful and fruitful discussions of the problem and friendful aid.
REFERENCES
Prof. A.A.Zenkin,
e-mail: alexzen@com2com.ru
WEB-Homepage: http://www.com2com.ru/alexzen