MATHEMATICS AND ART
"COGNITIVE-AESTHETIC IMAGES
OF
MATHEMATICAL ABSTRACTIONS"
by
Alexander and Anton Zenkins
“The World is a Number … and
Harmony of Singing Heaven Spheres”. – Pythagoras
“Mathematics is the Queen of the sciences and Number Theory is the
Queen of Mathematics.” - C.F.Gauss
"Die
naturlichen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk"
- Kronecker
“Almost all Mathematics can be deduced from the Natural
Number Conception” - Poincare

The ACTUAL INFINITY is a logical
and algorithmic basis of Cantor’s
diagonal argument as well as of all modern axiomatic set theories. However
during about two millenniums the “basis” was criticized and rejected by
ARISTOTLE: "There will not be an
actual infinite.The infinite has a potential existence.";
GAUSS: "I must protest most
vehemently against <the> use of the infinite as something consummated, as
this is never permitted in mathematics";
KRONECKER: "I
don't know what predominates in Cantor's theory - philosophy or theology, but I
am sure that there is no mathematics there";
POINCARE: "There
is no actual infinity; Cantorians forgot that and fell into contradictions.
Later generations will regard Mengenlehre as a disease from which one has
recovered ";
BROUWER: Cantor's
theory as a whole is "a pathological incident in history of mathematics
from which future generations will be horrified";
WITTGENSTEIN: “Cantor's argument has no deductive content at all”;
WEYL: the axiomatic set theory is a
“house built on sand”;
P.VOPENKA: “the set theory whose energies were directed to the actualization of
potential infinity turned out not to be able to eliminate the potentiality.
. .”, and a lot of others.
D.A.POSPELOV: “Certainly, there is something in all that .
. .” – said He and published in the famous Journal “NEWS OF ARTIFICIAL
INTELLIGENCE” the following quite scandal paper.

Abstract: The main aim of the presentation is to show that, according to G.H.Hardy, "beauty
is the first test: there is no permanent place
in the world for ugly mathematics" and that even high abstract mathematical conceptions and problems (e.g., a twice
abstract connection between the additivity and multiplicativity of natural
numbers, famous Waring's problem, continuum problem, discreteness and
continuity, finiteness and infinity, etc) can be made visible, beautiful,
attractive, and understandable. The dynamic images themselves of such
abstractions generated by means of Cognitive Computer Graphics (CCG)
visualization (see http://www.com2com.ru/alexzen)
turn out an effective tool to activate an intellectual intuition and the creative,
visual thinking of a human-being at the most high levels of cognition and to
generate really a paradigmatic new knowledge (so far) in a human-being’s mind.
There is an important problem of cognition of the World – the problem of the
natural Unity of the "anti"-symmetrical entities: Science and Art,
i.e., the Unity of the Left-Hemispheric (LF), rational, abstract thinking and
the Right-Hemispheric (RH), intuitive, visual one. When such the Unity takes
place the Humankind has the Ancient Greek Culture and the Age of Enlightenment,
else we have either a barbarism epoch or ... a lot of technocratic, man-caused
problems of modern civilization ... One of the ways to bring together a
creative intuition of the Art and a high abstract, formal, Left-Hemispherical
(LH) thinking of the Science is to make artistic and visible the high
abstractions of the modern Science.
The works will be presented as a computer demonstration on a large screen..
PARTICIPATION
IN PREVIOUS EXHIBITIONS:
1. Alexander A.Zenkin, Anton A.Zenkin, Exhibition
“Cognitive Visualization – Mathematics - Art”. – Congress of the Russian
Association of Artificial Intelligence. Institution for Control Problems of the
RAS, 19 November, 2003.
2.
Alexander A.Zenkin, Anton A.Zenkin, Exhibition “Mathematics and Art”. - The
First International Conference “p-Adic Mathematical Physics”, October 1-- 5,
2003, Steklov Mathematical Institute, Moscow, Russia.
3. Alexander A.Zenkin, Anton A.Zenkin, Exhibition of the SYMMETRY
FESTIVAL 2003 where Science Meets Art, 18-24 August, 2003, Budapest , Hungary.
4. Alexander A.Zenkin, Anton A.Zenkin, Presentation
"Intellectual Aesthetics of Mathematical Abstractions. The Unity
of the Left-Hemispheric, Rational, Abstract Thinking and the Right-Hemispheric,
Intuitive, Visual One". – The 5th International Congress
& Exhibition of the International Society for the Interdisciplinary Study
of Symmetry. Sydney, 8-14 July, 2001. Intersections of Art and Science. See at:
http://www.isis-s.unsw.edu.au/interact/gallery/image_files/zenkin/a_zenkin.html
5. Alexander A.Zenkin, Anton A.Zenkin, “Cognitive
Reality – A New Technology Of Scientific Cognition”. - FOKOM & POLITECHNICAL
MUSEIUM, Exhibition And Scientific Readings “Computer: The Frontier Of
Millenniums”. December 13, 2000.
6. G.I. Petushkova, Alexander A.Zenkin, and Anton
A.Zenkin, "Cognitive-Aesthetic images of the PI-Number and their
applications in fashionable woman's clothing." - International
scientific-industry conference "Actual problems of science, technology and
textile industry economics". Moscow, 2000.
7. Alexander A.Zenkin, Anton A.Zenkin, "Cognitive
Computer Graphics: Beauty and Truth of Mathematical Abstractions". -
International Conference and Exhibition "Mathematics and Art",
Suzdal, Russia, 1996. Proceedings, pp. 158-166 (1997).
8. Alexander A.Zenkin, Anton A.Zenkin, "Cognitive
Reality World: New Technology for Scientific Discoveries." -
International Federation of Artists, UNESCO, Institute of High Graphical
Investigations, Moscow Childish Club "Computer". - Exhibition-Seminar
"A Past-Future of Computer", 1999.


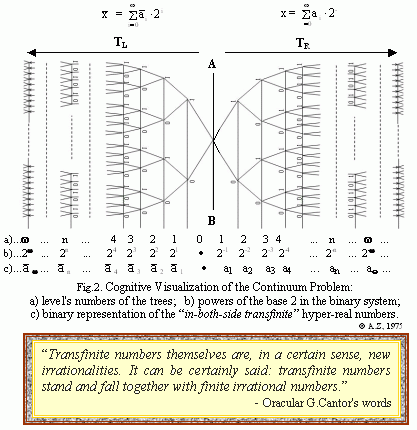

ARTISTIC SOLUTION
OF THE FIRST HILBERT PROBLEM ...


MYSTERIOUS LABYRINTHS
OF THE CONTINUUM PROBLEM

For more details see: A.A.Zenkin, Cognitive (Semantic) Visualization
Of The Continuum Problem And Mirror Symmetric Proofs In The Transfinite Numbers
Theory. - The e-Journal "VISUAL MATHEMATICS", Volume 1, No. 2, 1999, at: http://members.tripod.com/vismath1/zen/index.html


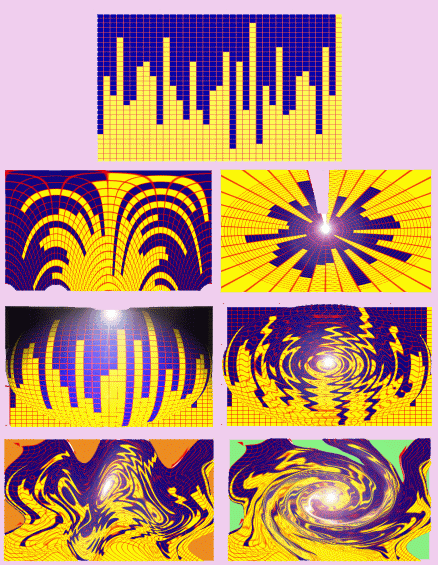
CCG-GENERALIZED WARING’S PROBLEM
The common problem:
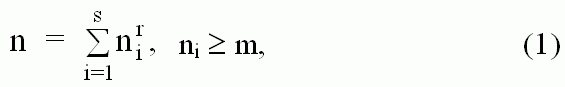
where m >= 0, r >= 2, s >= 1
- are fixed integers.
If m = 0, this
is the Classical Waring Problem (CWP), which was formulated in 1770 for the
first time. It was not until 1909 that D.Hilbert obtained his famous
number-theoretical result - he gave the complete solution to the CWP in the
form of the theorem presented in the left column of the Table 1 [1,2].
In the early 1980s, using methods of Cognitive Computer Graphics (CCG)
visualization [3-5], I saw (in the direct
sense of the word) for the first time and formulated the generalization of the
CWP to the case of any m ³ 0 and gave the complete solution to the
Generalized Waring Problem (GWP) in the form of the theorem, cited in the right
column of the Table 1 [3-7].
DEFINITIONS. For any m>=0, r>=2, s>=1, introduce two families of sets
of natural numbers:
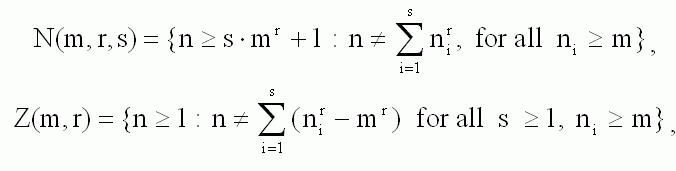
and the
following two arithmetic functions:

where |X|
denotes the number of elements of an arbitrary set X.

It is easy to see that in the special case m = 0 we obtain
the CWP:
![]()
Thus, for any m>=0, r>=2 and s>=g(m,r), the structure of
the sets N(m,r,s) is completely determined by the structure of the
corresponding sets, Z(m,r), - the so-called invariant sets of GWP.
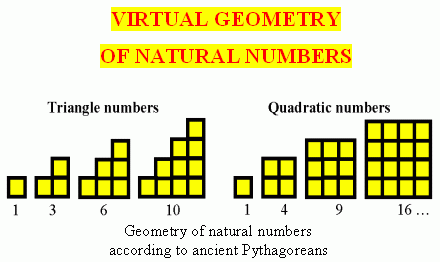
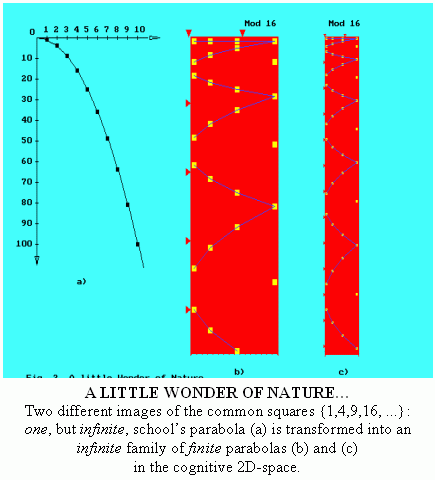
NEWCOMERS
FROM
THE WORLD OF NATURAL NUMBERS
By means of the most power Habble's Telescope, modern Science is searching for New-Comers
in the heart of the Far Cosmos ... But our high-intelligent
CCG-"Telescope" has found them in the very beginning of the
common series of the Godlike Natural Numbers...
Just these wise New-Comers pointed us the way to the beautiful Cognitive
Reality World of Natural Numbers and helped us to make a lot of wonderful
CCG-Discoveries.
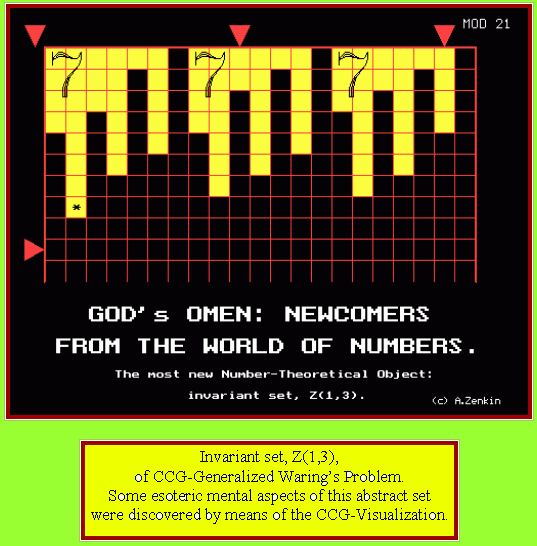


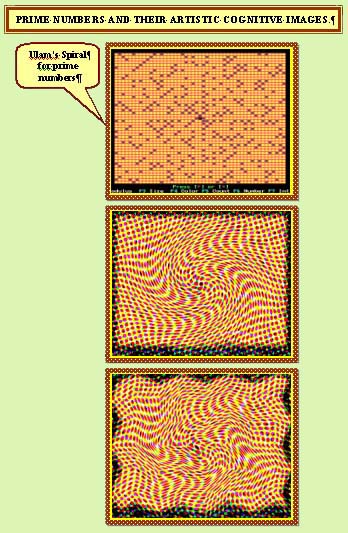
THE
ARTISTIC WORLD OF PRIME NUMBERS




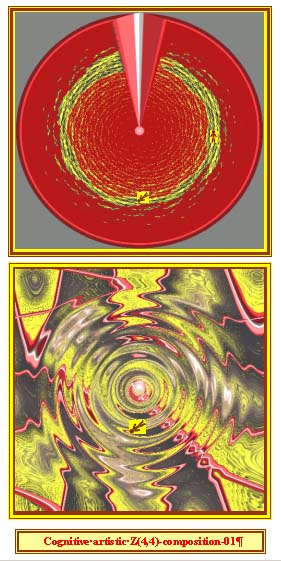
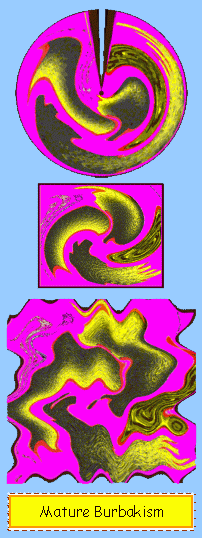
Artistic fantasy on the subject of the fatal anti-symmetry of
Left-Hemispheric (LH) and Right-Hemispheric (RH) thinking in modern meta-mathematics.
This dangerous mental illness of modern mathematical science and education is
called (by the Vice-President of the International Mathematicians Union,
Academician V.I.Arnold) a LH-Bourbakism <see at: http://www.com2com.ru/alexzen/papers/ng-02/contr_rev.htm>.
Its tragic artistic image is created from the initial CCG-pythogram of the
invariant set Z(4,4) of Generalized Waring’s problem. As it can be feelling,
the artistic LH-Bourbakism image conceals in self an evident “bacterial” threat
for a vivid natural intelligence of a human-being.
Академик В.И.Арнольд
о пагубных педагогических и социальных последствиях "бурбакизации"
математики: "В середине ХХ столетия обладавшая большим влиянием мафия
"левополушарных математиков" сумела <заменить> всю
содержательную сторону <математического образования> тренировкой в
формальном манипулировании абстрактными понятиями. ... Страшно подумать, какого
сорта влияние оказывают бурбакисты на (очевидно неглупых) студентов,
превращая их в формальные машины; ...абстрактное описание математики непригодно
ни для обучения, ни для каких-либо практических приложений, и ... даже опасно,
приводя к трагедиям типа Чернобыля. Несмотря на это, "левополушарные
больные" сумели вырастить целые поколения математиков, которые ...
способны лишь учить таким же образом следующие поколения. Результатом могут
стать массовый гипноз и социальные потрясения"



It is the p-number
pythogram under some new graphic transformation. The picture “Virtual Bronze
Object” allows us to feel a non-trivial 3D-dimension of that abstract
mathematical object, its bronze texture, and even thin blue coating of cuprum
oxide (patina) that is such typical for ancient artistic bronze wares.
For
details see at http://www.com2com.ru/alexzen/gallery/Gallery.html

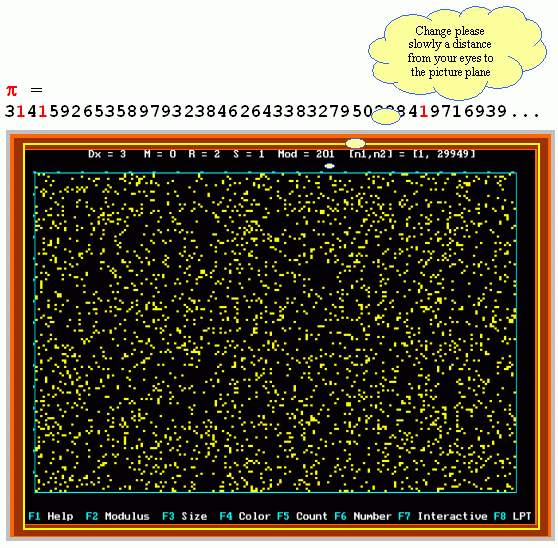
pz - incarnate faces of the p-number: in
dynamics, it is a boiling up symmetry of its decimal digits 0,1,...,9. A semantic
symmetry between our finite conciousness and the infinite nature of the number
is as follows: "IF YOU SCRUTINIZE INTO THE ABYSS NARROWLY AND FOR A LONG
TIME, THEN THE ABYSS ITSELF BEGINS TO PEER AT YOU . . .". Before a large
screen and by slow and rhythmic changes the pythogram scale (it’s also possible
to change slowly a distance from eye to picture), a user is plunged into the
dynamic, living, intellectual-aesthetic abyss and feels a positive
mental-therapeutical effect. Now we have a project to investigate such the
therapeutical properties of such the color-musical CCG-pythograms more
carefully.