WEB-site: http://www.com2com.ru/alexzen
 |
|
Incarnate faces of p
(from 0 to 9)
|
ALEXANDER & ANTON ZENKINS
Computing Center of the Russian Academy of Sciences
International Union of Artists
WEB-site: http://www.com2com.ru/alexzen
 |
|
Incarnate faces of p
(from 0 to 9)
|
644288109756659334461284756482337867831652........
 (C)
AZ
(C)
AZ
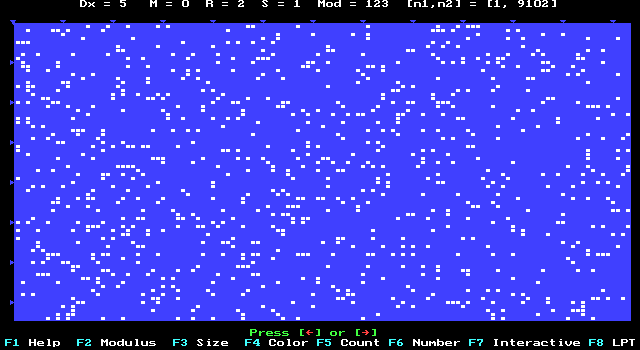
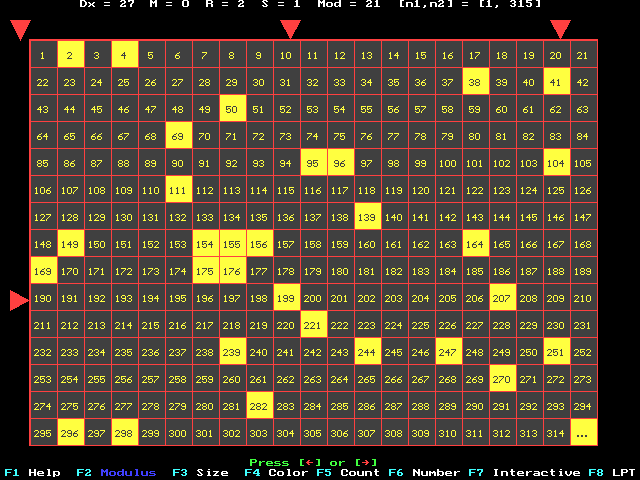
1. The Pythogram MODULUS is the quantity of numbers in any line.
2. The triangles over the first line and the left of the first column are
marks of tens of columns and strings correspondingly
3. The Pythogram modulus (shown as "Mod
= "),
the size of squares (shown
as "Dx = "),
and the colors are chosen
arbitrary.
4. Consecutively changing the modulus, we produce a unique computer p-film
on the dynamics properties of the transcendency notion.
5. We have a version of the computer films for p
, e, and any irrational numbers. But this is only
part of CCG-System PYTHAGORAS (Dialogue
System for Number Theory). This system can represent any kind of Number
Theory additive problems and produce computer mathematical CCG-films for NT-experts
as well as for a wide circle of scientists.
6. We have some p-projects
:
a) a video-film "Visual Comparison of the Cognitive Dynamical
Color-Musical Images (Pythograms) of the TRANSCENDENT, ALGEBRAIC, and IRRATIONAL
Numbers";
b) color-musical, mental-aesthetic p-THERAPY
of a soul;
c) and others.
7. Unfortunately we do not have a possibility to complete the project here,
so if you have been interested in a realization of such the project for science,
art, and education we are ready for a collaboration. Please, e-mail us:
alexzen@com2com.ru
For example, we can change the size of squares like this:
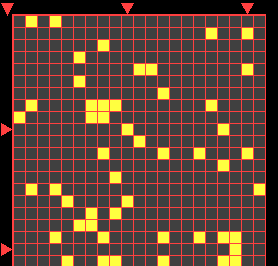 |
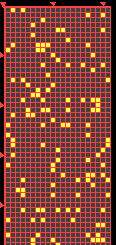 |
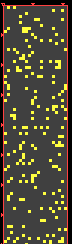 |
Now we can change the modulus:
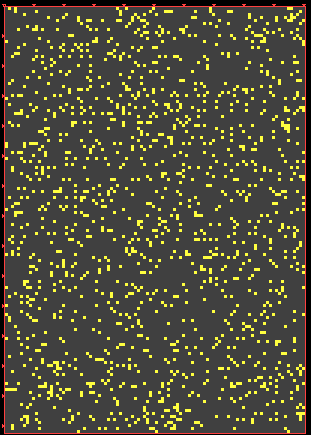 (C)
AZ
(C)
AZ
Or so:
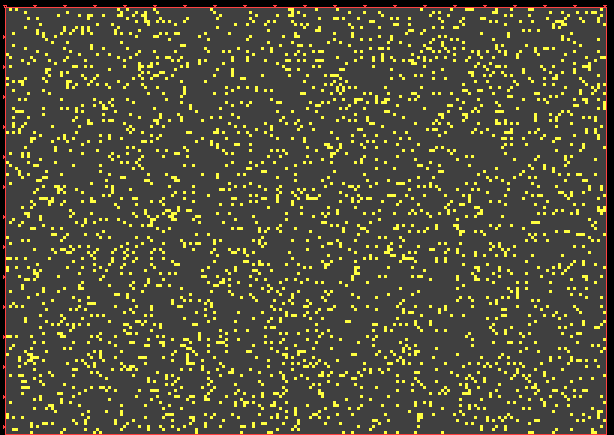 (C)
AZ
(C)
AZ
 |
 |
 |
IMPORTANT REMARK:
now we recommend to
change the screen distance
slowly back and forth from 3'' to 100''
to get the best cognitive effect. !!!
"0"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
AZ "1"-digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
AZ"2"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
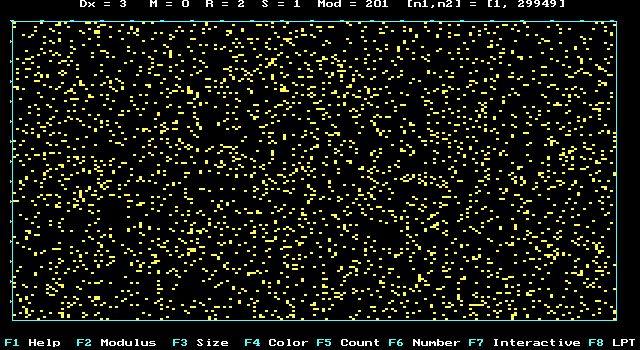
AZ "3"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
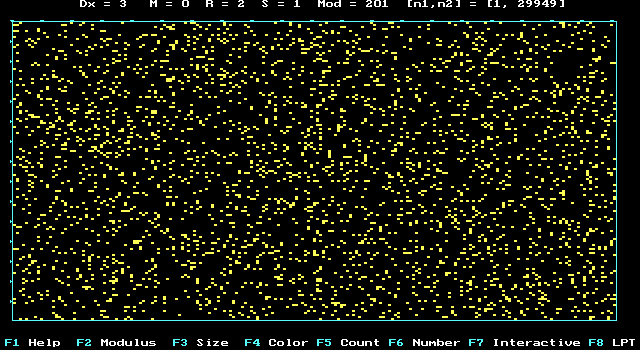
AZ "4"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
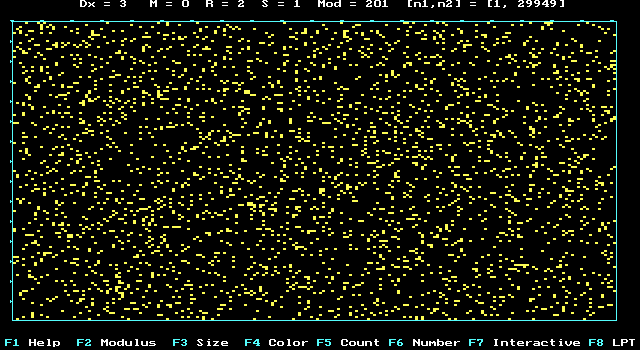
AZ "5"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
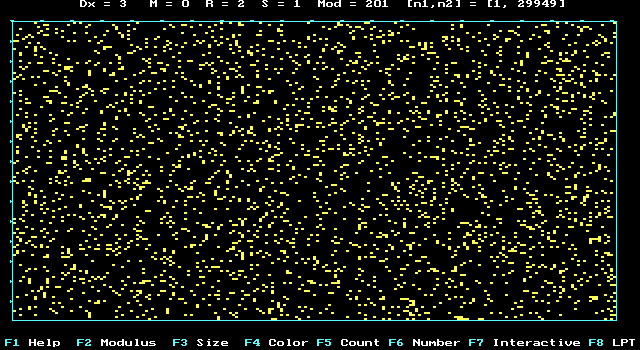
AZ "6"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
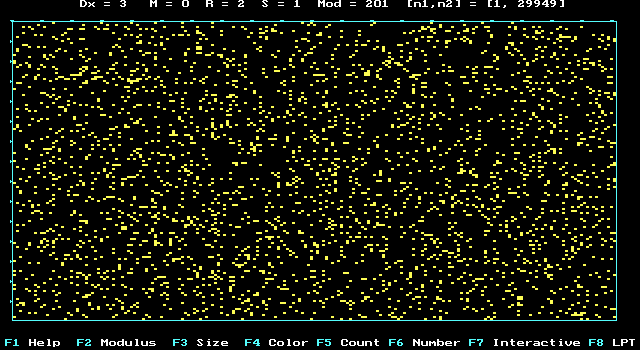
AZ "7"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
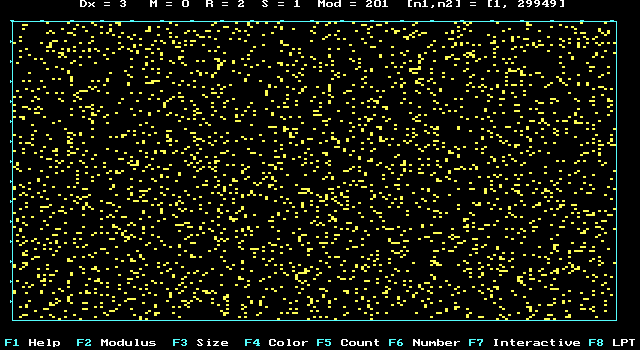
AZ "8"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
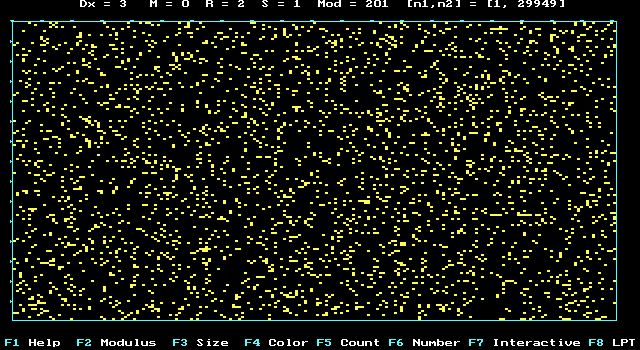
AZ "9"- digit in p-Number:
123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549303819
644288109756659334461284756482337867831652........
 ©
AZ
©
AZp -Number, an arbitrary colors. Dx=19.
 (C)AZ
(C)AZ
p -Number, an arbitrary colors. Dx=28. (a la Mandrian)
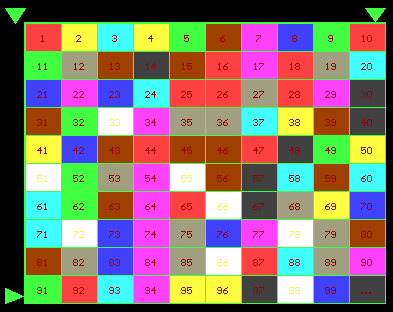 (C)AZ
(C)AZ
p -Number, an arbitrary colors. Dx=2.
 (C)AZ
(C)AZ
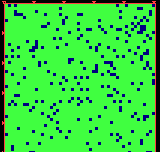
p-Number: even (red)/odd(blue)
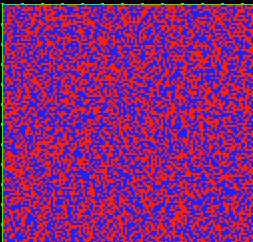 (C)AZ
(C)AZ
p-Number: even (red)/odd(yellow)
 (C)AZ
(C)AZ
Main difference of our CCG-approach to the visualization of the p-Number from the an artistic approach:
The CCG-approach preserves the mathematical structure of the p-Number, and the corresponding pythograms contain ALL information about mathematical properties of the p-Number. So, some new, today unknown properties of that p-Number can be re-constructed, discovered by means of the investigation of VISUAL features of corresponding CCG-pythograms of the p-Number.
p-Number:
even (yellow)/odd(gray)
 (c) AZ
(c) AZ
GOLDEN SECTION
GoldSection: an arbitrary colors
(for every digit - its individual color.) 123456789*123456789*123456789*123456789*123456789*
16180339887498948482045868343656381177203091798..
 (C)AZ
(C)AZ
. 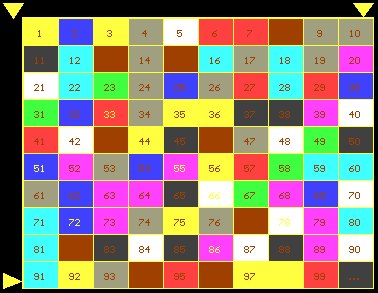 (C)AZ
(C)AZ
Golden Section: even (YELLOW)/odd(RED)
 |
|
Magma
|
(C)AZ
Golden Section: even (blue)/odd(red)
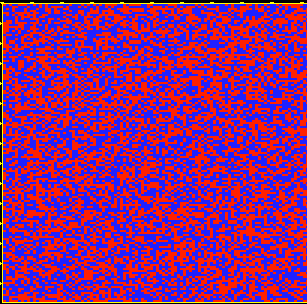 |
|
Mosaic
|
"p"
x "e"
= for any i=1: if p[i]
= e[i] then BLACK else WHITE
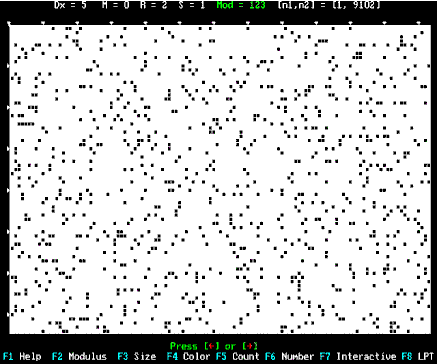 (C)AZ
(C)AZ
"p" x "GS" = for any i=1: if p[i] = GS[i] then BLACK else WHITE
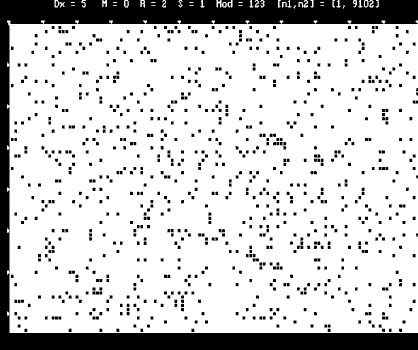 (c)AZ
(c)AZ
"e" x "GS" = for any i=1: if e[i] = GS[i] then BLACK else WHITE
 (c)AZ
(c)AZ
"p"
x "e" x
"GS" = for any i=1: if p[i]
= e[i] = GS[i] then
BLACK else WHITE
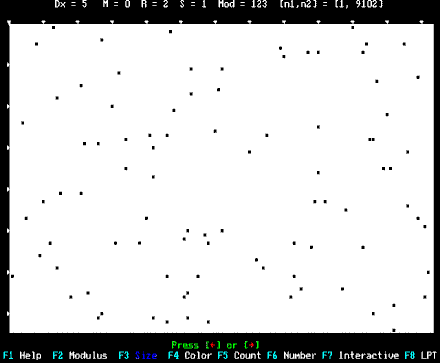
"p"
x "sq2" = for any i > 1: if p[i]
= sq2[i] then WHITE else BLUE