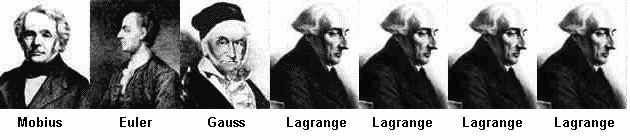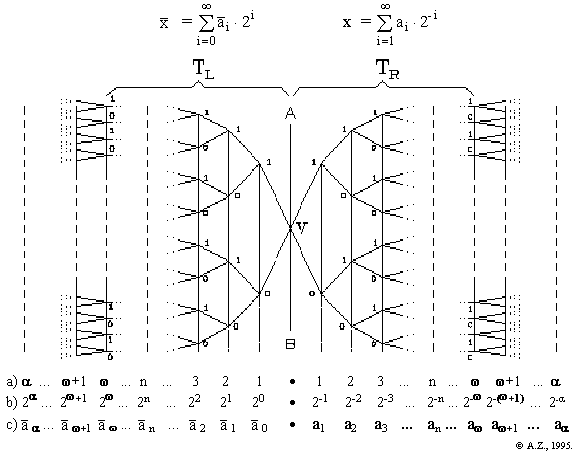COGNITIVE REALITY

is a NEW CCG-TECHNOLOGY

OF SCIENTIFIC COGNITION.

by

Alexander A. Zenkin

– Prof., Doctor of Physical and Mathematical Sciences, Leading Research Scientist, Department of Theoretical Problems of Artificial Intelligance, Computing Center of the Russian Academy of Sciences, the member of the Russia Philosophical Society, the member of the International Creative Union of Artists

Anton A. Zenkin
– PhD, CCG-systems developer, project manager.

MAIN THESIS:

FROM VIRTUAL REALITY TO COGNITIVE REALITY . . .
BASING ON NEWEST MULTI-MEDIA THECHNOLOGIES
OF THE COGNITIVE SEMANTIC COMPUTER VISUALIZATION.

ILLUSTRATIVE GRAPHICS

(http://www.bartleby.com/65/li/LibertyS.html)

AIM: PHOTOGRAPHIC-REALITTY, RECOGNITION.

ONLOOKER'S REACTION: «HOW THIS LOOKS LIKE AS . . .!»

THE IMAGE INTERPRETATION
IS REALIZED IN "TERMS" OF A GENETIC DATA BASE IMPRINTED
IN OUR SUBCONSCIOUSNESS (OUR PAST EXPERIENCE).

 

COGNITIVE GRAPHICS.

AIM: GENERATING NEW KNOWLEDGE.

IMPORTANT REMARK:
we recommend to change the screen distance slowly back and forth from 3'' to 100''
to get the best cognitive effect. !!!

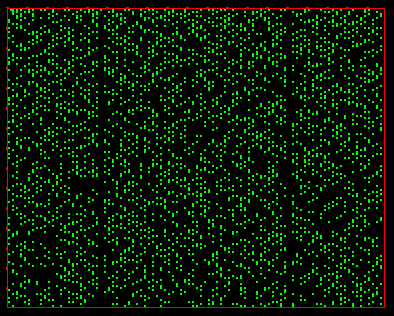
p -Number: the 1-digit is yellow, all others are black

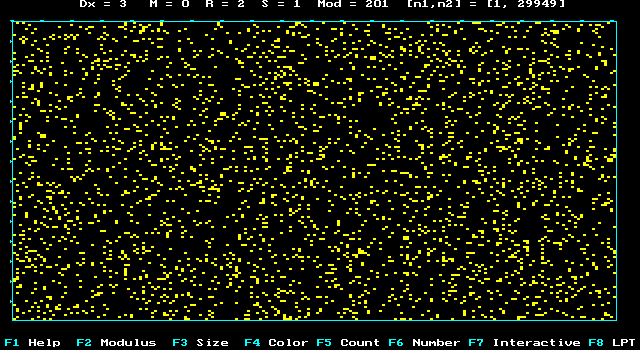
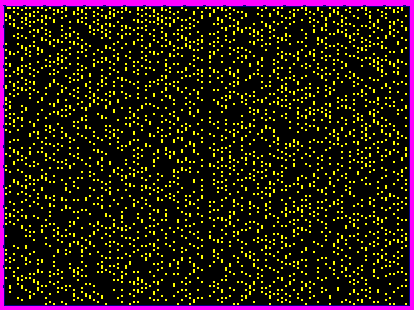
p -Number: even digits are red, odd digits are yellow

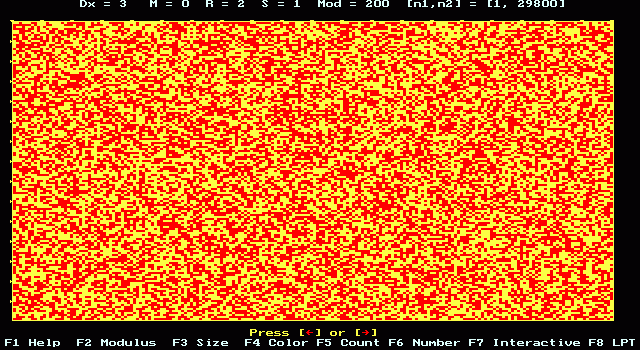
ONLOOKER'S REACTION: «AND WHAT DOES THAT MEAN . . .?!»

THE IMAGE UNDERSTANDING
IS IMPOSSIBLE
WITHOUT ITS EXPLICIT INTERPRETATION
IN "TERMS" OF A GIVEN PROBLEM DOMIAN.

 

 


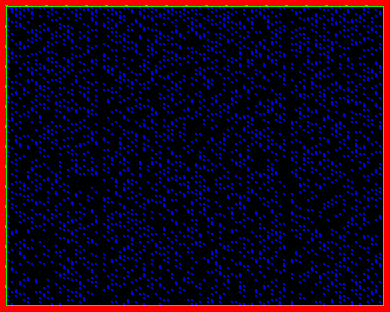
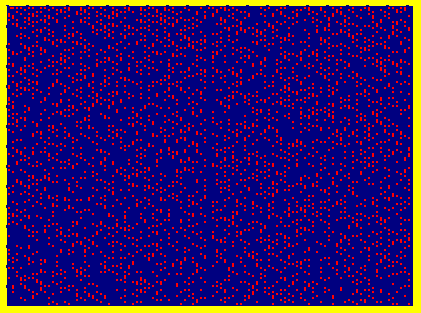
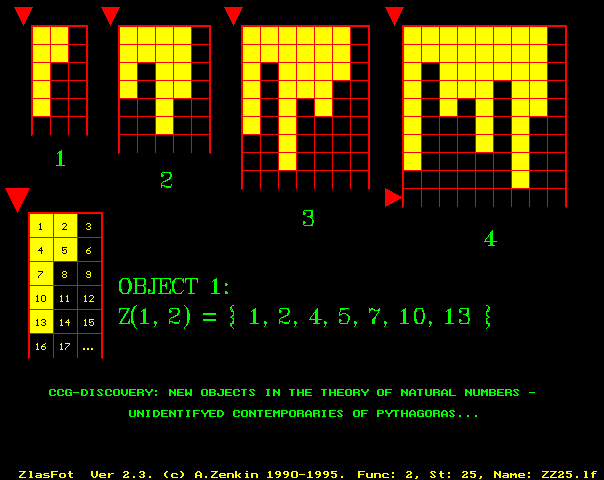
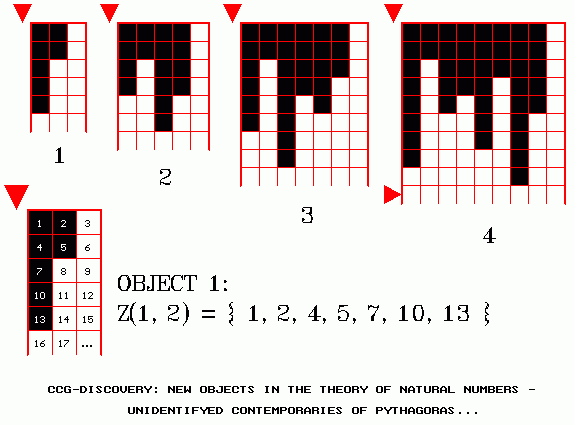
These two are the same well known discrete number-theoretical object – Prime Numbers set.

DEFINITION OF THE PYTHOGRAM

Df. 1. The pythogram is a color-musical 2D-image of an abstract Number-Theoretical (NT) object.
Df. 2. NT-object is a segment of the 1D-series of natural numbers, with a NT-predicate P(n), n ³ 1, defined on it.
Df. 3. The sense of the Number Theory consists (by B.N.Delone) in the very difficult to comprehend connection between the additive and multiplicative properties of natural numbers.

CCG-TECHNIQUE:

·         Color all natural numbers in according with the rule: if P(n) then color-1 else color-2.

·         Convert the 1D-series of natural numbers into the 2D-image (Table).

·         Make musical such 2D-image in according with a function: F(n, P(n), place, value, any other NT-Properties of n, and so on).

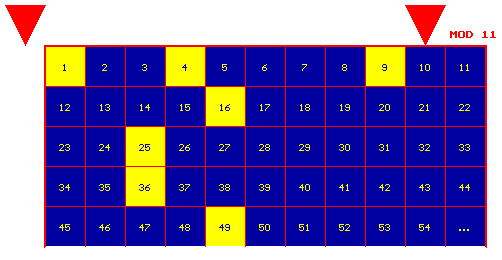
Pythogram of the segment [1,54] of the natural number series by modulus 11.
Here, NT-predicate P(n) = "n is a square of a natural number".

 

MAIN PYTHOGRAM PROPERTIES:

 

COGNITIVE EXPLANAITION
OF THE CCG-VISUALIZATION TECHNOLOGY

with the predicate P(n) = "n is a square of a natural number" as an example.

 

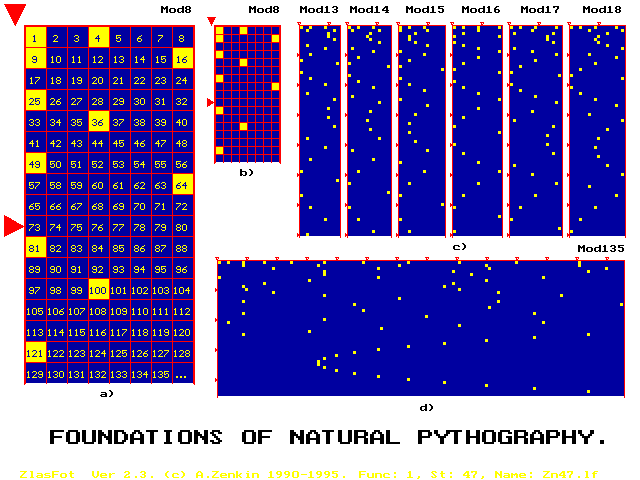
So, consider again the well-known from the Pythagoras time, monotonic, some "dull" series of natural numbers, 1,2,3,...,n, ... , with the predicate P(n) = "n is a natural square". All natural numbers of the series are colored here accoding to the simple rules: "IF P(n) is true, THEN n is yellow, ELSE n is blue". The quantity of numbers in a row of the pythogram (a so-called modulus of the pythogram) we can choice arbitrary, and let it will be here equal to 8 (see Fig. a). As is know, there are too many natural numbers, therefore particular numbers are not of interest for us: we shall erase them by decreasing size of cells (Fig. b). This allows us to increase greatly the surveyed area. The modulus of the pythogram is a unique degree of freedom: changing the modulus we produce a CCG-movie about a NT-predicate P(n) as a whole image (Gestalt). Some frames of that movie you can see in Fig. c. Such CCG-Movies permit first to see unknown geometrical properties of abstract mathematical structures (Fig.d): you can see these beautiful dynamic transformations of the same mathematical object - of the well-known set of squares {1,4,9,16,25,36,49,...}.

CCG-METHODOLOGY (SEMIOTICS OF CCG-IMAGES):

            General scheme of CCG-investigations:

WATCH

a pythogram or CCG-movie;

SEE

graphic features of the pythogram;

INTERPRET

these graphic features in terms of a given problem domain;

FORMULATE

a CCG-statement;

GENERALIZE

that CCG-statement;

PROVE

a new mathematical theorem.

Remark here, that using exactly this CCG-technique, we could generalize the most famous number-theoretical achievement of D.Hilbert - his complete solution (1909) of Classical Waring's Problem (1770) - see below.

INTELLECTUAL
CCG-INSIGHTS
INTO THE COGNITIVE WORLD
OF NATURAL NUMBERS

for more info see:
http://www.com2com.ru/alexzen/
and
ARTISTIC p -NUMBER GALLERY
Cognitive Semantic Visualization of the p -Number :
http://www.com2com.ru/alexzen/gallery/Gallery.html

Quadratic Holography
of Natural Numbers …

THE GREAT PYTHAGORAS' DREAM:
THE WORLD AS A HARMONIC UNITY OF NUMBER, IMAGE, AND MUSIC.

Remind once more: when you are looking at the pythograms,
change slowly the distance to the screen.

During more than 3000 years, the Humankind is "staring at" such the "trivial" and exhaustively investigated mathematical object, as the set of squares of natural numbers:

1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26, … (1)

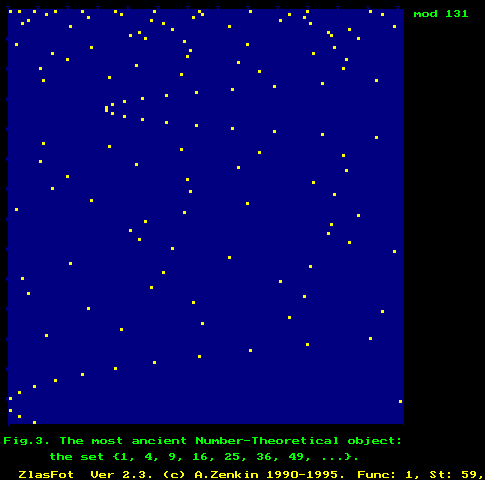
            The pythogram modulus is a unique degree of our freedom: changing the modulus, we create a CCG-movie, which is not only interesting from the point of view of the mathematical and intelligent aesthetics, but which permits us to see new dynamic properties of abstract NT-structures. As a rule, such the dynamic mathematical properties are simply incomprehensible in statics! One of the frames of this CCG-movie (by mod=131) is shown in the next Fig. We can see here a number of surprising new and non-trivial NT-facts (virtual geometrical objects).

A frame of the CCG-movie about a lot of unknown dynamic properties of the well-known series (1) of natural numbers (here by modulus 131). - If you are not in raptures about seeing this highest intellectual-aesthetic Wonder of the Natural Numbers World (almost by H.Hesse’s "Das Glassperlenspiel": remember about NT-Music!), then Mathematics is not your vocation...

 

LEIBNIZ'S BLUE DREAM:
TO AWAKE A THOUGHT BY MEANS OF FIGURES...

In the far "non-computer" epoch, great Gotfried Leibniz supposed that "figures are useful to awake a thought". The CCG-technology open unique opportunities just for awakening a non-traditional mathematical thought. We suggest some not quite ordinary examples.

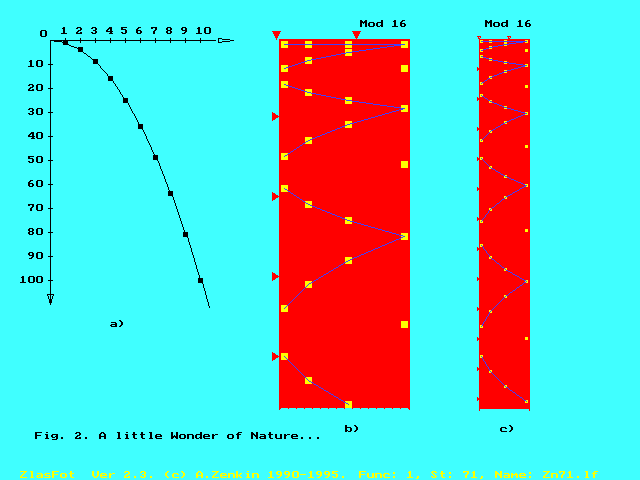
The most beautiful and unexpected CCG-Discovery: traditional (a) and non-traditional (b,c) forms of the visual representation of one and the same mathematical object - of the well-known natural squares set, {1, 4, 9, 16, 25, 36, ...}. We have got a certain new "paradox" in modern mathematics: a distance between a) and b) is equal to ... about 2000 years! To draw b) could even Pythagoras. In 1841, Meobius drew very similar parabolas, even by the modulus 16 (!), in his known nomographical works for a graphic multiplication of integers. But only CCG allows us to see for the first time this fantastic transformation: one, but infinite parabola is transformed into the infinite family of finite parabolas ! – That is not only a number-theoretical fact, but it is a deep philosophical event. - More details as to the virtual geometry of natural numbers see here.

PRIME NUMBERS PYTHOGRAMs

Even modern Mathematics does not know what law of nature generates the prime numbers.
But if that law exists in reality, then you now are looking at how it works!.
Possibly, just such the pictures will help anybody of you to understand the mathematical nature of the law
and to formulate it directly now. :-)

WARING'S PROBLEM

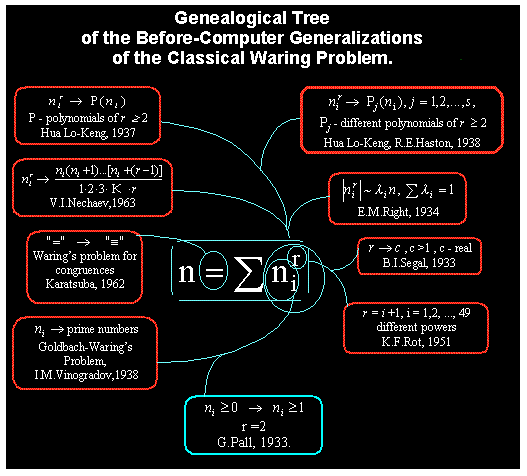
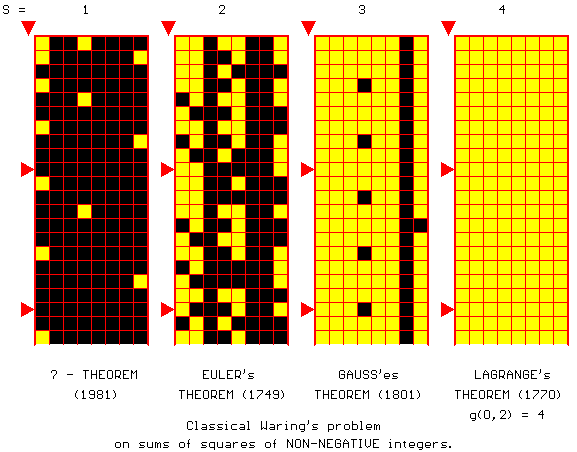
CLASSICAL WARING's PROBLEM (1770):

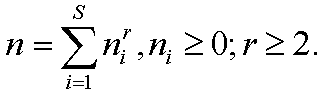   (1)

WARING'S HYPOTHESIS. For any fixed r³ 2, there is a minimal number of summands, say, s=g(r) such that any natural number n³ 1 is representable as a sum (1) for any s ³ g(r).

CCG-GENERALIZED WARING's PROBLEM (1980):

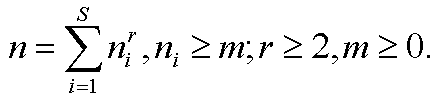   (2)

COMMON PROBLEM OF ADDITIVE NUMBER THEORY.
Given fixed m³ 0, r³ 2, s³ 1. What n³ 1 are representable and what aren't by sums (2)?

GENERELIZED WARING'S PROBLEM.
For any fixed m³ 0, r³ 2, there is a minimal number of summands, say, s=g(m,r) such that any natural number n³ n0(m,r,s) is representable as a sum (2). – Details see below.

Some main publications:

1. A.A.Zenkin, Cognitive Computer Graphics. Applications in Classical Theory of Natural Numbers. (Synopsis) - Moscow: "NAUKA", 1991, 191 pp.
2. A.A.Zenkin, Waring's problem from the standpoint of the cognitive interactive computer graphics. - Math. & Comput. Modelling, Vol.13, No.11, 9 - 36, 1990.
3. A.A.Zenkin, Waring's problem: g(1,4) = 21 for fourth powers of positive integers.- Comput. & Math. with Applics, Vol. 17, No. 11, 1503 - 1506, 1989.

FOR HIGH NT-EXPERTS:

4. A.A.Zenkin, Main CCG-results as to the Generalized Waring's Problem. - on e-mail request (~800Kb)

 

A mathematical puzzle: show, please, what so far was not generalized in this problem?

 

A STORY ABOUT CCG-DISCOVERY OF GENERALIZED WARING'S PROBLEM.

         Consider the problem on the representation of natural numbers n ³ 1 by sums of the form

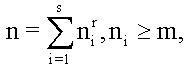                      (1)

where m ³ 0, r ³ 2, s ³ 1 - are fixed integers.

         If m = 0, this is the Classical Waring Problem (CWP), which was formulated in 1770 for the first time. Euler, Lagrange, Gauss, Legandre and many other outstanding mathematicians of XVIII-XX CC. (which were possessed of the eminent scientific intuition!) were investigating the Classical Waring Problem (CWP) during more than a hundred years. However, only in 1909, the greatest German mathematician David Hilbert gave the complete solution of CWP (see Table 1, the left column).

Table 1. Logical and semantical isomorphism of classical and non-classical Waring's problem.

CLASSICAL WARING's PROBLEM
(D.Hilbert, 1909)

GENERALIZED WARING's PROBLEM
(A.Zenkin, 1979)

For the fixed m = 0
and for every r ³ 2
there exists:
1) the finite smallest number of summands,
g(r) º g(0,r),
-
such that for any s ³ g(0,r):
N(0,r,s) = Æ

For any m = 1, 2, 3, ...
and for every r ³ 2
there exist:
1) the finite smallest number of summands,
g(m,r),
2) the finite invariant set, Z(m,r) ¹ Æ ,
such that for any s ³ g(m,r):
N(m,r,s) = {s× mr +z : zÎ Z(m,r)}

HERE: for arbitrary values of the parameters m ³ 0, r ³ 2, and s ³ 1, the following two families of sets of natural numbers are defined:

,

,

and the following two arithmetic functions:

where |X| denotes the number of elements of an arbitrary set X.

            In general, the traditional mathematics "was staring" at the Classical Waring Problem (CWP) more than 200 years. However, only CCG-visualization has allowed us to see the completely unexpected fact, that the CWP represents only the 0-floor of a much more general ¥ -floor problem - so called Generalized Waring's Problem (GWP) (see Table 1, the right column). - Why not "a relativity theory" of the traditional mathematical values! - Can’t we now formulate (and prove!) the famous classical (m=0) Lagrange theorem for every m=1,2,3,...?!

CLASSICAL (m=0) AND GENERALIZED (m=1,2,3, ...) WARING's PROBLEM

 

THE DRAMATIC HISTORY
OF CLASSICAL NUMBER THEORY IN 1749 – 1801

Classical Waring’s Problem for sums of squares: m=0, r=2.
Here, by s ³ 4, we can see the famous Lagrange's Theorem on four squares (1770):
g(0,2)=4, i.e. any natural n ³ 1 is a sum of s squares for any s³ 4.

 

Classical Waring's Problem for sums of cubes: m=0, r=3.
Here, by s ³ 9, we can see the famous Wieferich's Theorem
on nine cubes (1909): g(0,3)=9,
i.e. any natural n ³ 1 is a sum of s cubes for any s³ 9.
By s=7, we can also see the famous Linnik's Theorem (1943)
on seven cubes: G(0,3) £ 7.

 

THE FIRST BEFORE COMPUTER ERA STEP
FROM CLASSICAL (m=0) TO GENERALIZED (m=1)
WARING'S PROBLEM FOR SQAURES (r=2)
MADE BY AMERICAN MATHEMATICIAN G.PALL (1933)

 

G.PALL’s THEOREM (1933). By any s ³ 6, any natural number n ³ 1 is representable as a sum of exactly s squares of positive integers, except for the numbers 1,2,3,..., s-1, and those of the form s + {1,2,4,5,7,10,13}.

THE SECOND AND NEXT STEPS
FROM CLASSICAL (m=0) TO GENERALIZED (m=1)
WARING'S PROBLEM FOR CUBES (r=3)
1979

 

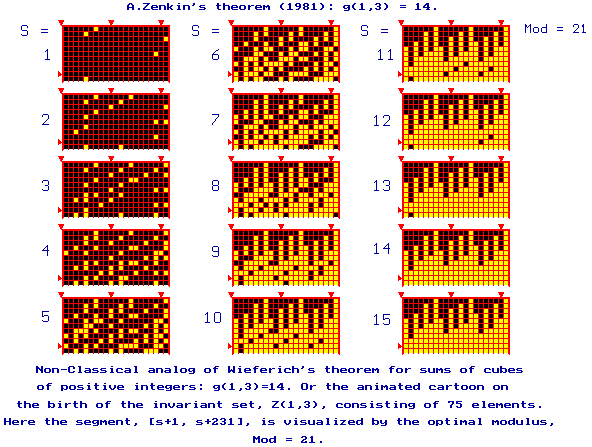
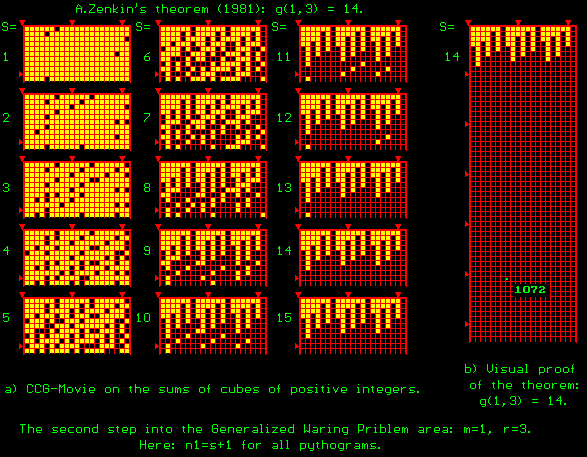
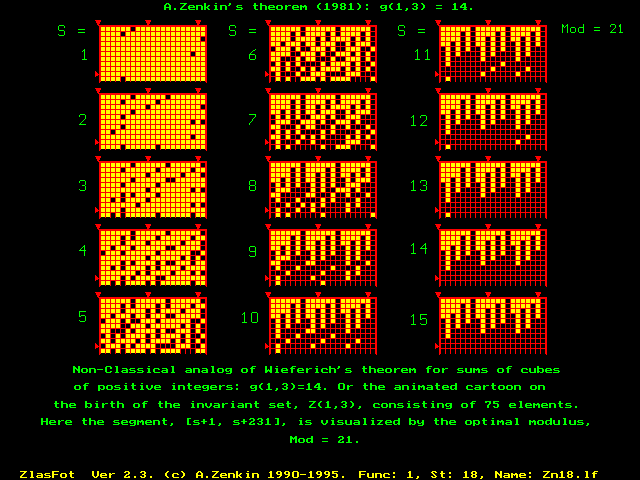
A.ZENKIN’s THEOREM (1979). For any s ³ 14, any natural number n ³ 1 is representable as a sum of exactly s squares of positive integers, except for the numbers 1,2,3,..., s-1, and those of the form s + Z(1,3), where the set, Z(1,3), is known explicitly.

CCG-DISCOVERY

OF NEW NUMBER-THEORETICAL OBJECTS
IN THE VERY BEGINNING
OF THE COMMON SERIES
OF COMMON FINITE NATURAL NUMBERS

Color-musical pythograms of new mathematical objects, discovered by CCG-approach:
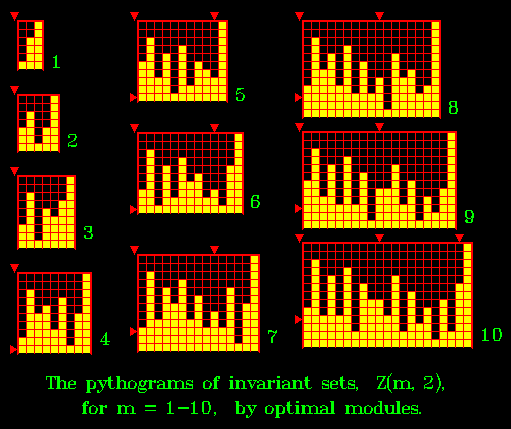
some invariant sets of Generalized (m=1,2,3,4) Waring's Problem for squares r=2.
The first representative of this infinite family, Z(1,2), was discovered by G.Pall in 1933.

 

OTHER NEW OBJECTS OF THE SAME FAMILY r = 2,
BUT WITH DIFFERENT m = 1-10.

 

 

NEW FAMILY OF OBJECTS
for cubes r=3.

The invariant set of Generalized Waring's Problem,
Z(1,3) = {all yellow numbers: 1-6,8-15, ... 149}.

 

 

 

The same object Z(1,3) by different modules.
Or CCG-movie about dynamic NT-properties of the invariant set, Z(1,3),
of Generalized Waring's Problem.
Any NT-expert can see here at least three absolutely new NT-theorems.

 

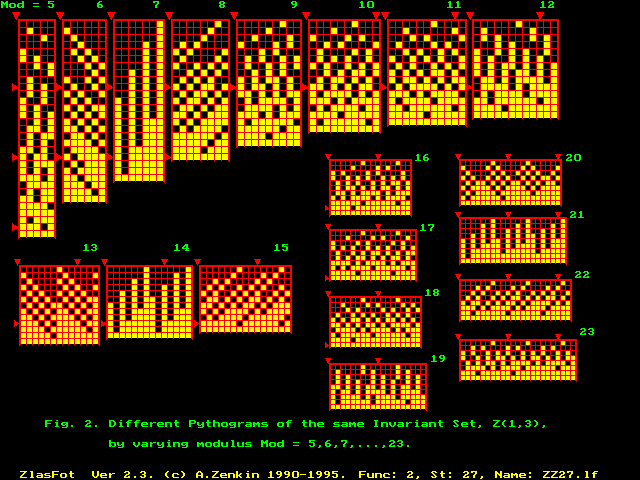
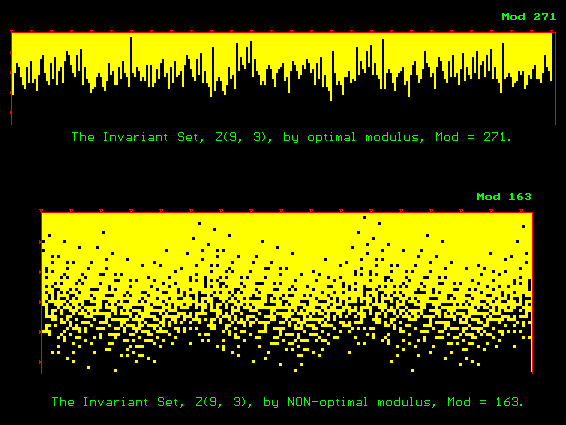
COMPARE THE OPTIMAL MODULUS WITH A NON-OPTIMAL ONE
FOR NEW NT-OBJECTS Z(9,3).

Our experience shows that such the pythograms by non-optimal modulus are usually very beautiful from the intellectual aesthetics point of view, but their mathematical interpretation is not always obvious. On the contrary, the pythograms by optimal modulus are usually not only semantically fine, but as a rule demonstrate quite explicitly new unexpected features of abstract mathematical structures visually. The CCG-System Pythagoras is able now automatically to search for such the optimal modulus of pythograms (solving a discrete optimal control problem with a formalized "Semantical Beauty" as an optimization criterion), to search for new mathematical facts, and to formulate new mathematical statements in a printed form customary for publication in matheamtical journals. : -)

The CCG-searching of a semantically beautiful (optimal) modulus (here mod 8),
and formulation of the mathematical result.

EXAMPLE 1. Gausses Theorem about sums of three squares (1801).

 

 

 

 

COMPARISON OF VALUES OF THE FUNCTION G(m, r)
FOR ANY m ³ 1 WITH THE CLASSICAL CASE m = 0.

HYPOTHESIS. " m³ 0 " r³ 2 [ G(m, r) º G(0, r) ] ???.

COUNTER-EXAMPLE.

    1. LAGRANGE’S THEOREM (1770). g(0,2) = 4, i.e. N(0,2,4) = Æ .

 

COROLLARY 1. G(0,2) £ 4.

GAUSS’ THEOREM (1801). " n ³ 1 { if n = (8k+7)× 4l, k, l = 0, 1, 2, ...
then n Î N(0,2,3) }, i.e. |N(0,2,3)| = ¥ .

COROLLARY 2. G(0,2) > 3.
COROLLARY 3. G(0,2) = 4.

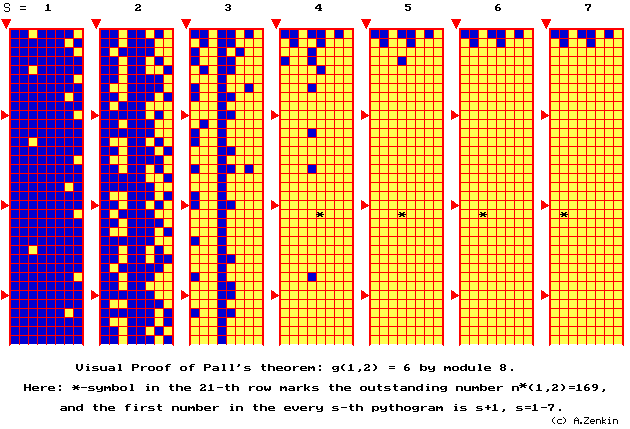
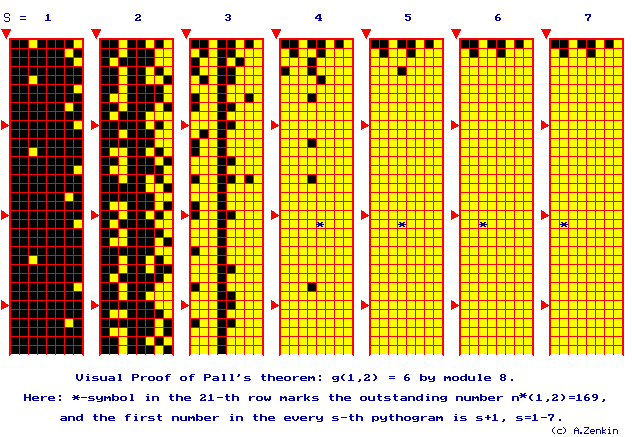
B) G.PALL’S THEOREM 1 (1933). g(1,2) = 6, and |N(1,2,5)| < ¥ .

 

 

COROLLARY 4. G(1,2) £ 5.

DESCARTES’ THEOREM. " n ³ 1 { if n = (2, 6, 14)× 4l, k, l = 0, 1, 2, ...then n Î N(1,2,4) }, i.e. |N(1,2,4)| = ¥ .

COROLLARY 5. G(1,2) > 4.
COROLLARY 6. G(1,2) = 5.

So, we have proved:

G.PALL’S THEOREM 2 (1933). G(1, 2) > G(0, 2).

The Theorem shows that the Hypothesis " m³ 0 " r³ 2 [ G(m, r) º G(0, r) ] (see above) is false, and consequently, the transition from any m to m+1 is non-trivial.

 

GENERALIZATION OF THE CLASSICAL WARING PROBLEM.

G.PALL’s THEOREM (1933). By any s ³ 6, any natural number n ³ 1 is representable as a sum of exactly s squares of positive integers, except for the numbers 1,2,3,..., s-1, and the numbers of the form s + {1,2,4,5,7,10,13}.

G.PALL’s THEOREM 2. By s=5, any natural number n ³ 1 is representable as a sum of exactly 5 squares of positive integers, except for the numbers 1,2,3,4, 5+{1,2,4,5,7,10,13} and the number 33.

 

A.ZENKIN’s THEOREM (1979). For any s ³ 14, any natural number n ³ 1 is representable as a sum of exactly s squares of positive integers, except for the numbers 1,2,3,..., s-1, and the numbers of the form s + Z(1,3), where the set, Z(1,3), is known explicitly.

for more information:
Zenkin A.A. Waring's problem from the standpoint of the cognitive interactive computer graphics. - Mathematical and Computer Modelling, Vol.13, No. 11, pp. 9 - 25, 1990.
Zenkin A.A. Some picturesque generalizations of Nechaev-Waring's problem obtained by means of cognitive interactive computer graphics. - Mathematical and Computer Modelling, Vol.13, No. 11, pp. 27 - 36, 1990.
                 Zenkin A.A. Waring's problem: g(1,4) = 21 for fourth powers of positive integers.- Computers and Mathematics with Applications, Vol.17, No. 11, pp. 1503 - 1506, 1989.
                Zenkin A.A. Generalized Waring's Problem: G(m,r)£ G(0,r) +m+1 for any m ³ 1, r ³ 3. - Doklady Mathematics, vol 56, No. 1, pp. 499-501 (1997). Translated from Doklady Akademii Nauk, Vol 355, No. 2, 1997, pp. 151 - 153.

CCG-DISCOVERY

OF
A NEW UNIVERSAL PROPERTY
OF
COMMON NATURAL NUMBERS.

FOR MORE INFO SEE

http://www.com2com.ru/alexzen/papers.html#pub2

 

GENERALIZED WARING’S PROBLEM:
NEW UNIVERSAL PROPERTY OF NATURAL NUMBERS.

1980: GWP: n =, ni ³ m, where m ³ 0, r ³ 2, s ³ 1 - fixed integers.

1933: PALL’S THEOREM. By m=1, " s ³ 6 " n ³ 1 ( n = , ni ³ 1 ),
except for 1, 2, ..., s-1, and s+z, z Î Z(1,2) = {1, 2, 4, 5, 7, 10, 13}.

1964: W.Sierpinski, "Elementary Theory of Numbers". - Warsaw, 1964.

         Page 379: there is Pall’s theorem (1933) formulation and its complete proof.
         Page 380: there is

FACT 1. The number 169 = , ni ³ 1, simultaniously for all
         s = 1 ¸ 155, 157, 158, 160, 161, 163, 166, 169.

1993:

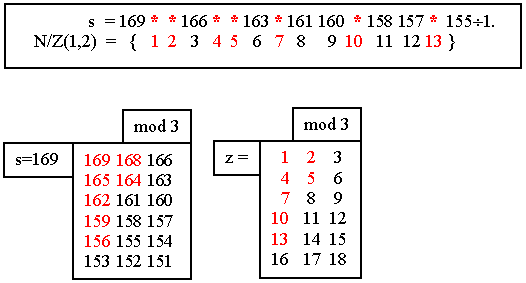
         So, all the necessary information to discover this new property of natural number was presented in the pages 379 and 380 of the Sierpinski monography which was a handbook of almost every mathematician during many years from 1964. But nobody could see this Fact 1. Only CCG-visualization allowed us to see the following

CCG-PROMPT: s ¹ 169 - z, z Î Z(1,2).

and

CCG-FACT 1a. 169 = , ni ³ 1, by all s, 1 £ s £ 169, except for s = 169 - z, z Î Z(1,2).

CCG-FACT 2.      The numbers like 169 are: 132, 152, 172, 252, 302,... - in all 35 numbers among the first hundred.

Ó A.Z., 1995.

FUNDAMENTAL UNIVERSAL PROPERTIES
OF NATURAL NUMBERS.

1. "TO SUCCEED" (the Definition of the Natural Number Concept) :

" n $ ! ( n + 1).

2. MULTIPLICATIVE REPRESENTATION :

" n $ ! ( n = ),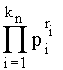

where all pi, 1 £ i £ kn, are different prime numbers, and all ri³ 1.

3. ADDITIVE REPRESENTATION ( New Property ):

" n $ ( n = 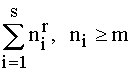) simultaniously for all s, 1 £ s £ n,

EXCEPT FOR :    1) all s > [n/mr ];
2) all s: n= s × mr + z, z Î Z(m,r);
3) possibly, some s < g(m,r).

Visual explanation of the new property sense:

         Fixe any integers m³ 1, r³ 2. Then any natural number n is representable as a sum (*) simultaneously for all s, A £ s < B, where A=g(m,r) and B = n - max{Z(m,r)}. Whether this n is or isn't representable as a sum (*) for s < A and s ³ B is unambiguously defined by the main parameters g(m,r) and Z(m,r) of the Generalized Waring's Problem.

            So, the new additive universal property of natural numbers gives a complete solution of the problem about the number of representations of any n > m by sums of r-th powers of ni ³ m by any fixed r³ 2, m³ 1.

For more information see: Zenkin A.A., Generalized Waring’s problem: about one new property of natural numbers. - "Math. Zametki", vol. 58, No.6, 372 - 378 (1995).

Ó A.Z., 1995

CLASSICAL NUMBER THEORY

AS A NEW DIRECTION

OF CELLULAR
CCG-AUTOMATA

A NEW VERSION OF
JOHN CONWAY'S

"THE GAME OF LIFE"

for more info see

COGNITIVE COMPUTER GRAPHICS AND CELLULAR AUTOMATA

NUMBER THEORY AND CELLULAR AUTOMATA

HERE: John Conway's "The Game of Life" configurations

           

 

EXAMPLE.

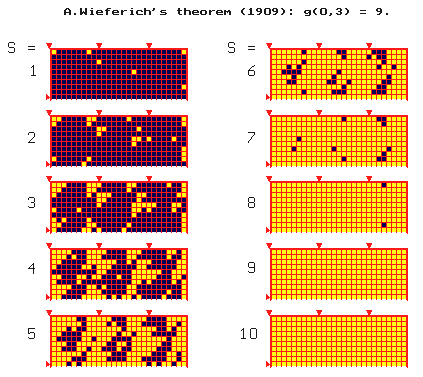
Gauss' Theorem (1801). By m=0, r=2, any natural number, n, is a sum of three cubes of non-negative integers (here - yellow), EXCEPT FOR the numbers of the form (here - black): n = 4l (8k + 7), by all l,k = 0,1,2, ,… .

Zentralblatt fur Mathematik: 753.11045 ( 1993 ?)
Zenkin, A.A., Cognitive computer graphics. Applications in Theory of Natural Numbers. Ed. by D.A.Pospelov. (Russian. English summary);[B] Moskva: Nauka. 192 p. (1991). [ISBN 5-02-014143-7]
This book contains an exposition of the author's approach to studying abstract number-theoretic problems using techniques of interactive computer graphics. Mostly he has examined Waring's problem and its generalizations [see the review of his paper in Math. Comput. Modelling 13, No. 11, 9-25 (1990) below for a detailed discussion of the procedure in this case […], the use of pythograms seems to be a valid and useful metaprocedure for stimulating intuition. Since the pythograms look like cellular automata, the reviewer wonders what the relationship is. [ J.S.Joel (Kelly) ]

 

CLASSICAL WARING'S PROBLEM AS A CELLULAR AUTOMATON.

         All additive Number Theory can be re-formulated in the cellular automaton language in the following way. In general, our cellular automaton field is a two-dimensional matrix (table) with M column (the modulus of the CCG-image) and the infinite numbers of strings.
In practice (due to natural computer graphics limits) the modulus M and a number of strings N are limited by not very large finite values. However, using a window-technique, we can visualize and look through quite large and distant segments [n1, n2] of the Natural Numbers series, or what is the same, - of that cellular automaton field.
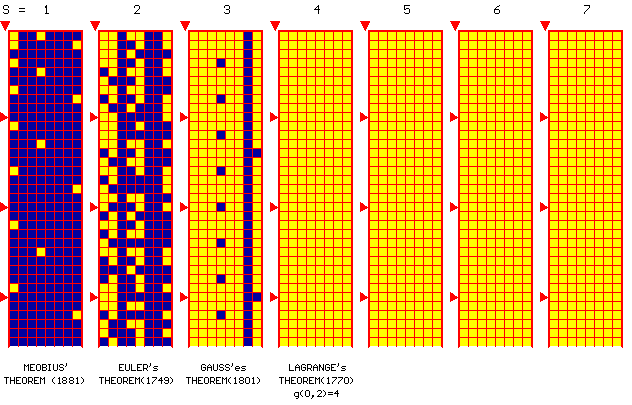
For the simplest case r=2, the initial state-configuration (s=1) of our cellular automaton is defined by the predicate:

P(n;r;s) = P(n;2;1) = "n is a sum of ONE square".

         Now we define the following simplest, but very natural rule for generating next step-configurations of our cellular automaton, which is defined by the formulation itself of the Classical Waring's Problem and by the nature itself of Natural Numbers: for any s ³ 1 and for any n ³ 1:

IF P(n; 2; s) is true THEN P(n+k2; 2; s+1) is true too, where k=0,1,2, …

         So, beginning from the initial configuration S1 (by s=1) and changing the parameter s (a time analog), we can now generate the following sequence of automata configurations:

            S2 (s=2): the corresponding CCG-image (a cellular automaton state) represents the famous Euler's Theorem (1749) on sums of two squares;
            S3 (s=3): the corresponding CCG-image (a cellular automaton state) represents the famous Gauss'es Theorem (1801) on sums of three squares;
            S4 (s=4): the corresponding CCG-image represents the famous Lagrange's Theorem (1770) on sums of four squares;
S5=S6= . . . - the corresponding CCG-images (a cellular automaton states) are the same and we have a stationary "point" of our cellular automaton.

            So, the simple sequence (CCG-movie) of the cellular automaton configurations {S1, S2, S3, S4, …} shows us a whole half-century history (1749-1801) of Classical Waring's Problem.

COMMON CASE. For any m=0, r³ 2, s³ 1,

P(n;r;s) = "n is a sum of s r-th powers",

and the transformation rule is:

IF P(n; r; s) is true THEN P(n+k2; r; s+1) is true too, where k=0,1,2, …

 

SUPER-INDUCTION:

NEW LOGICAL METHOD
FOR MATHEMATICAL PROOFS
WITH A COMPUTER

for more info see

SUPER-INDUCTION METHOD:
LOGICAL ACUPUNCTURE OF MATHEMATICAL INFINITY.
XX WORLD CONGRESS OF PHILOSOPHY. PAIDEIA Project ON-Line

(at the PAIDEIA-site) http://www.bu.edu/wcp/Papers/Logi/LogiZenk.htm
SEE also: http://www.philosophy.ru/library/fm/zenkin.html (in Russian)

In 1949, German mathematician H.E.Richert proved the following quite strange inductive statement [1]: "IF there exists a natural number, say, n* such that Q(n*) is true THEN for any natural number n>n* P(n) is ture", or in a short symbolic notation:

         [$ n*Q(n*)] ® [" n>n*P(n)],                (1)

where P and Q=f(P) are two collections of number-theoretical properties of common finite natural numbers (or predicates given on the natural numbers set).
So, the H.E.Richert Theorem (further - EA-Theorem) is a mathematical, i.e., authentic, proof of the inductive statement of the quite unusual form: "from a SINGLE statement, [$ n*Q(n*)], to a COMMON one, [" n>n*P(n)]".

         In 1978, using Cognitive Computer Visualization of mathematical abstractions technology [2], I discovered two new different classes of such the EA-Theorems and formulated the Super-Induction (SI) method [3]. By means of the SI-method, a lot of conceptually new scientific results was obtained in Classical Number Theory [ 4 ]

         Note some unexpected connections of SI-method with some basic logical conceptions.

         1. According to inductive J.S.Mill's Logic, we always can formulate a common statement, say, H basing on a set of particular facts, but such H will always be only a plausible statement. The existence itself of EA-Theorems (1) and SI-method show that the main inductive Logic paradigm is broken in some areas of discrete mathematics.
2. The Aristotle's modus ponens rule sounds so: [A&[A® B]] ® B. Mathematical Logic and meta-Mathematics consider the implication [A® B] as a deductive inference of a less common consequence B (e.g., a theorem) from a more common premise A (e.g., an axiom system). SI-method generalizes the "modus ponens" rule to the case when the premis A is a single statement, but the consequence B is a common one.
3. It can be easy shown, that the SI-method generalizes the classical complete mathematical induction B.Pascal's method. Moreover, SI-method works well there where B.Pascal's method simply does not work [5].
4. Cognitive Visualization of mathematical abstractions and SI-method allow, by certain conditions, to use corresponding cognitive images as quite legitimate arguments in rigorous mathematical proofs, i.e., they realize an authentic ostensive proofs in, say, L.E.J.Brouwer's sense [3, 6, 7].

         The project was supported by G.Soros' ISF (grant ZZ5000/114; the title: "Cognitive Computer Graphics – a New Window In the World Of Cognition".), RHSF (grant 98-03-04348; the title: "Cognitive Computer Graphics: New Approaches In Logic And Philosophy Of Mathematical Infinity") and RBSF (grant 98-01-00339; the title: "Cognitive Computer Graphics: New CCG-Technology For a New Scientific Knowledge Generation").

REFERENCES.

1. Richert, H.E., Uber Zerlegungen in paarweise vershiedene Zahlen, Norsk Mat. Tidssk. 31 (1949), pp. 120-122.
2. A.A.Zenkin, Cognitive Computer Graphics. Applications in Theory of Natural Numbers. - Moscow: "NAUKA", 1991, 191 pp.
3. A.A.Zenkin, Superinduction: A New Method For Proving General Mathematical Statements With A Computer. - Doklady Mathematics,Vol.55,No.3, 410-413 (1997).
4. A.A.Zenkin, Waring's problem from the standpoint of the cognitive interactive computer graphics. - "Math. & Comput. Modelling", Vol.13, No.11, 9 - 36, 1990.
5. A.A.Zenkin, Waring's problem: g(1,4) = 21 for fourth powers of positive integers.- Comput. & Math. with Applics, Vol. 17, No. 11, 1503 - 1506, 1989.
6. A.A.Zenkin, Super-Induction Method: Logical Akupuncture of Mathematical Infinity. - XX WCP. Paideia. Boston, U.S.A., 1998. Proceedings, Section "Logic and Philosophy of Logic".
7. A.A.Zenkin, Cognitive Graphics for Obtaining New Knowledge. - Proceedings On Workshop on Russian Situation Control and Cybernetic/Semiotic Modelling, Edr. Robert J. Strol, Columbus,Ohio, U.S.A., pp. 79-100 (1996).

 

THE LOGICAL SCHEME OF THE SUPER-INDUCTION METHOD.

1. It is required to prove the COMMON statement: " n³ 1 P(n).
2. We construct (today - invent !) an apt new predicate Q(n) and design the following CONDITIONAL statement (so-called EA-Theorem):

        [$ n*Q(n*)] ® [" n>n*P(n)],         (1)

where Q = f (P), and Q ¹ P.
3. We prove (ANALYTICALLY) that conditional statement (1).
4. We search for (usually, with a computer, but it is not forbided manually, if any!) natural number n* ( it is enough to find one of such numbers), possessing the unique set of the number-theoretical properties Q(n*).

IF we have found such the unique number n*, THEN:

5. We have proved the reliable truth of the antecedent of the implication (1), that is the single statement, $ n*Q(n*).
6. By MODUS PONENS rule, we conclude:

$ n*Q(n*), $ n*Q(n*) ® " n>n*P(n) |- " n>n*P(n),

i.e., we have proved the reliable truth of the consequent of the implication (1), that is the common statement, " n>n*P(n).
7. For all n £ n*, we check up the truth values of P(n) (as a rule, with a computer, by means of the corresponding CCG-picture or manually - that is not essentially for the reliability of such the checking up), and produce a set,

Ne = { n £ n* : Ø P(n) },

of exceptional elements.
8. Thus, we have proved the common mathematical statement:

" n Î N P(n), EXCEPT FOR " n Î Ne = { n £ n* : Ø P(n) }.

REMARK. If the set, Ne is empty then we have proved the traditional: " n³ 1 P(n).

REFERENES:
A.A.Zenkin, Superinduction: a New Method for Proving General Mathematical Statements with a Computer. - Doklady Mathematics, Vol.55, No.3, pp. 410-413 (1997).

SUPER-INDUCTION METHOD GENERALIZES
THE B.PASCAL'S MATHEMATICAL INDUCTION METHOD.

According to: N.Bourbaki, Set Theory, - Moscow : Mir, 1965, pp. 199 (in Russian). Complete Mathematical Induction Method (CMIM) (or "Induction Principle" by NB):

C61.  [P(0) & [" n [P(n) ® P(n+1)]]] ® " n P(n),
[P(n0) & [" n [P(n) ® P(n+1)]]] ® [ " n> n0 P(n) ],
where, usually, the number n0 is equal to either 0 or 1.
Denote
Q(n0) º P(n0) & [" n [P(n) ® P(n+1)]],
then (by the meta-mathematical $-introduction rule)
Q(n0) |- $ n*Q(n*),
and we have got formally:

         [ $ n* Q(n*) ] ® [ " n > n* P(n) ],

that is we obtain a version of the Super-Induction Method !

         Thus,
1) the Super-Inuduction Method is the generalization of the Complete Mathematical Induction Method by B.Pascal.
2) the statement C61 of the Complete Mathematical Induction Method by B.Pascal is the most ancient EA-Theorem.
3) the Super-Inuduction Method has demonstrated that modern meta-matheamtics is not an adequate description for classical mathematics.

 

COMPARATIVE ANALYSIS
OF
B.PASCAL’s MATHEMATICAL INDUCTION
AND
SUPER-INDUCTION METHOD

B.PASCAL'S MATHEMATICAL INDUCTION METHOD

A.ZENKIN'S
SUPER-INDUCTION METHOD

1. P(n) is given.

1. P(n) is given.

2. The Problem: " n P(n) ?

2. The Problem: for what n P(n) ?

3. P(0), P(1), P(2), ..., P(k), -
are checked , usually, by a hand.

3. Q = f(P) -
is invented, discovered.

4. " n [P(n)® P(n+1)] - is proved analytically without a computer.

4. [$ n*Q(n*)] ® [" n>n*P(n)] - is proved analytically without a computer.

5. " nP(n) - is proved.

5. n* is searched for , usually, by a computer.

 

6. " n>n*P(n) - is proved

 

7. Verifying P(n) for every n £ n* by a computer, as a rule.

 

8. " n³ 1 P(n), except for
Ne={n £ n*: Ø P(n)}, is proved.

Commentary:
A Computer is not required for the Complete Mathematical Induction Method AT ALL.

Commentary:
Here n*=n*(m,r) for any m³ 1,r³ 2 !!!
As a rule, today, the SI-Method can not be used without a computer in order to FIND OUT the n*.

THE SUPER-INDUCTION METHOD.
EA-THEOREMS. EXAMPLE 1.

         EA-Theorems are a new type of logical and mathematical statements.
The Finiteness Criterion for the Invariant Sets, Z(m,r), which are defined as following:

Z(m,r) = { n³ 1 : n ¹ by any s³ 1, ni ³ m }.

EA-THEOREM 1. For any m ³ 1, r ³ 2,

IF      $ n*Q(n*) where Q = (i) & (ii) & (iii) and

(i).    n* Î Z(m,r);
(ii).    n* + i Ï Z(m,r) for every i=1,2,...,k;
(iii).   k ³ (m+1) r -m r,

THEN         " n>n* P(n) where P(n) = " n Ï Z(m,r) ",

i.e. n*=max{Z(m,r)} and |Z(m,r)| < ¥ .

PROOF (by Reductio ad Absurdum method). See Superinduction: a New Method for Proving General Mathematical Statements with a Computer

Now, using the EA-Theorem 1, we have:

m=1, r=2; k ³ (1+1)2 - 12 = 4 - 1 = 3.
m=2, r=2; k ³ (2+1)2 - 22 = 9 - 4 = 5.
m=3, r=2; k ³ (3+1)2 - 32 = 16 - 9 = 7, and so on,

 

and looking at the corresponding pythograms of the invariant sets Z(m,r), we can find out the corresponding "threshold" natural numbers n*(m,2) and prove visually (i.e., ostensively) the finity of these setts.

THE FINITENESS CRITERION
FOR THE INVARIANT SETS, Z(M,R). EXAMPLE 1a.

THEOREM 1*) . For any m ³ 1 and r ³ 2,
          IF     $ n*Q(n*), where Q = (i) & (ii) & (iii) and

         (i). n* Î Z(m,r);
         (ii). n* + i Ï Z(m,r) for any i = 1, 2, ... , k;
         (iii). k ³ (m + 1)r - mr ,

         THEN         " n>n* P(n),

         where P(n) = " n Ï Z(m,r) ".

------------------------------------------------------------------------------------

*) Zenkin A.A. Some Extensions of G.Pall's Theorem. - Computers and Mathematics with Applications, Vol.9, pp.609-625 (1983).

EXAMPLE 1.

Here, for invariant set, Z(1,3), k=(1+1)^3 - 1^3 = 7, and we can see that n*(1,3) = 149. It proves that the last (maximal) element of Z(1,3) is 149.

 

 

            By means of the most power Habble's Telescope, modern Science searches for New-Comers in the heart of the far Cosmos… But our high-intelligent CCG-"Telescope" has found them in the very beginning of the common series of the Godlike Natural Numbers...
Just these wise New-Comers pointed us the way to the beautiful Cognitive Reality World of Natural Numbers and helped us to make a lot of wonderful CCG-Discoveries.

ESTIMATION OF THE FUNCTION G(m,r)

BY MEANS OF THE FUNCTION g(m-1,r). EXAMPLE 3.

THEOREM 2*). For any m ³ 1 and r ³ 2,

            IF        $ n*(m,r) Q(n*(m,r)), where Q = (i) & (ii) & (iii) and

         (i). n*(m,r) = , ni ³ m,
         (ii). for all s = s0 , s0 + 1, s0 + 2 , ... , s1 ,
         (iii). s1 - s0 ³ g(m-1, r),

THEN         " n > n0(m,r) P(n), where

P(n) = " n = , ni ³ m, s* = g(m-1,r) + s0 ,

so that

G(m,r) £ g(m-1,r) + s0 ,

n0(m,r) = n*(m,r) + (g(m-1,r) + s0 )× (m-1)r + max { Z(m-1,r) }.

---------------------------------------------------------------------------------------------------------------

*) Zenkin A.A. Waring's problem from the standpoint of the cognitive interactive computer graphics. - Mathematical and Computer Modelling, Vol.13, No.11, pp.9 - 25 (1990).

EXAMPLE 3.

ã A.Z. 1995

 


INTELLECTUAL AESTHETICS OF MATHEMATICAL ABSTRACTIONS

CCG-TECHNOLOGY for COGNITIVE SEMANTIC
SCIENTIFIC VISUALIZATION

123456789*123456789*123456789*123456789*123456789*
31415926535897932384626433832795028841971693993751
05820974944592307816406286208998628034825342117067
98214808651328230664709384460955058223172535940812
84811174502841027019385211055596446229489549 . . .

 

Pythogram of the p -Number's 1-Digit.
It's being read (counted) from left to right, and from top to bottom.

 

 

 

THROUGHOUT FULL OF HOLES CONTINUUM:

From the Language of Abstractions to the Language of CCG-Images.
And backwards.

Alexander A. Zenkin, Anton A. Zenkin,

"Languages of Science – Languages of Art", Collection of scientific papers. –"Progress-Tradition", Moscow, 2000, pp. 172-179.

1. COGNITIVE SEMANTIC VISUALIZATION
OF THE CONTINUUM PROBLEM.

"Transfinite Numbers themselves are, in a certain sense, new irrationalities. Indeed, in my opinion, the method for the definition of finite irrational numbers is quite analogous, I can say, is the same one as my method for introducing transfinite numbers. It can be certainly said: transfinite numbers stand and fall together with finite irrational numbers."

Georg Cantor.

 

 

 

Fig.1 Cognitive-visual image of Continuum Problem:
a) the enumeration of the levels of the trees TR и TL;
b) powers of 2 – the basis of binary system;
c) the binary representation of the "transfinite-infinite-in-both-directions" of hyper-real numbers of modern non-standard analysis.

For more info see: A.A.Zenkin, Cognitive (Semantic) Visualization Of The Continuum Problem And Mirror Symmetric Proofs In The Transfinite Numbers Theory. - The e-journal "VISUAL MATHEMATICS" at the WEB-Sites: http://www.mi.sanu.ac.yu/vismath/zen/index.html
http://members.tripod.com/vismath1/zen/index.html

e-mail: alexzen@com2com.ru
HomePage: http://www.com2com.ru/alexzen