Невыпуклые задачи

Пусть - определенная на скалярная функция, а вектор-функция действует из в . Функции и будем считать дифференцируемыми в интересующих нас точках. Производные в точке будем обозначать как и . Производная - -мерный вектор, т.е., элемент , а - линейный оператор, действующий из в , т.е, в конечномерном случае, матрица размера . Рассмотрим следующую задачу:

Задача 4.

,

.▄

Определение 7. Допустимая по ограничениям точка называется точкой локального минимума задачи 4, если найдется окрестность точки такая, что из следует . Если же выполняется строгое неравенство , точка называется точкой строгого локального минимума. ▄

Определение 8. Допустимая по ограничениям точка называется точкой глобального минимума задачи 4, если из следует . Если же выполняется строгое неравенство , точка называется точкой строгого глобального минимума. ▄

Определение 9. Функция , где , а , называется функцией Лагранжа задачи 4. ▄

Согласно приведенным выше определениям, любая точка глобального минимума является также и точкой локального минимума. Обратное, для произвольной задачи, вообще говоря, не верно, хотя встречаются классы задач, для которых это так. Например, у задач линейного и выпуклого программирования, любая точка локального минимума является также и точкой глобального минимума. (Почему?).

Далее мы будем интересоваться условиями достижения в точке локального минимума задачи 4.

С задачей 4 будем связывать следующую линеаризованную в точке задачу

Задача 5.

,

.▄

Определение 10. Будем говорить, что ограничения задачи 4 в точке удовлетворяют условию Слейтера, если ограничения линеаризованной в этой точке задачи (задачи 5) удовлетворяют условию Слейтера определения 3. Такую точку будем называть невырожденной.

Теорема 10. Пусть - точка локального минимума задачи 4, и ее ограничения в этой точке удовлетворяют условию Слейтера, тогда - точка глобального минимума задачи 5.

Доказательство. Предположим, что - точка локального минимума задачи 4, но найдется , такой что и . Пусть - вектор, на котором выполняется условие Слейтера для задачи 5, т.е., . Положим . Тогда, в силу выпуклости аффинного оператора для всех справедливо , а в силу непрерывности линейного функционала , при достаточно малых будет выполняться . Зафиксируем . Рассмотрим луч . На этом луче и . Следовательно, для достаточно малых будет выполнено и , что противоречит тому, что - точка локального минимума задачи 4. Полученное противоречие и доказывает теорему. ▄

К задаче 5, как к задаче выпуклого программирования применимы все результаты соответствующего раздела, т.е., если 0 – решение этой задачи, то найдется вектор , такой что будет выполнено:

.

(18)

Полагая в (18) , получаем , отсюда и из заключаем:

.

(19)

Мы получили условие дополняющей нежесткости.

Далее, из того что (18) справедливо для любого , учитывая (19), получаем:

,

(20)

где - линейный оператор, сопряженный , действующий из в .

Для задачи 5 естественно ввести функцию Лагранжа следующим образом:

.

(21)

Из (18), (19) следует, что точка есть седловая точка функции Лагранжа (21) задачи 5, т.е.,

. Далее, нетрудно заметить, что функция Лагранжа (21) линеаризованной задачи, есть производная в точке функции Лагранжа исходной задачи: .

Окончательно сформулируем, полученные результаты.

Теорема 11. (Необходимые условия локального минимума нелинейной задачи, или теорема Куна-Таккера для нелинейной задачи). Пусть - точка локального минимума задачи 4, и ее ограничения в этой точке удовлетворяют условию Слейтера, тогда найдется вектор , такой что будет выполнено (19) и (20), а точка будет седловой точкой производной в точке функции Лагранжа задачи 4 (21). ▄

Определение 11. Допустимую ограничениями задачи 4, невырожденную точку будем называть стационарной, если для нее найдется вектор множителей Лагранжа , такой что будет выполнено (19),(20).

Ограничения типа равенства

Рассмотрим вариант задачи 4, где вместо требуется . В случае ограничений типа равенства, роль условия Слейтера, обеспечивающего содержательность результатов, играет условие Люстерника, которое состоит в следующем:

Определение 12. Для ограничений задачи в точке выполняется условие Люстерника, если линейный оператор отображает на все . (Т.е., в конечномерных пространствах, ранг матрицы равен ). ▄

Замечание. Невыполнение условия Слейтера или Люстерника в экстремальной задаче с ограничениями, содержательно означает, что множество допустимых значений задачи занимает не все измерений пространства , а целиком лежит в некотором его подпространстве. Тогда любой ортогональный этому подпространству вектор отделяет это множество от любой точки , и можно получить соотношение, формально имеющее вид (6) с , но содержательно отражающее лишь факт нахождения ОДЗ задачи целиком в некотором подпространстве пространства . Чтобы получить в этом случае содержательные результаты, нужно перенести рассмотрение задачи в это подпространство, или в подпространство еще меньшей размерности, если окажется, что и в данном подпространстве, ОДЗ лежит в некоторой его гиперплоскости. ▄

Для задачи с ограничениями типа равенства, справедливы результаты подобные полученным для задачи 4. При доказательстве теоремы, аналогичной теореме 10, существенно используется следующая

Теорема 12. (Люстерника) Пусть, пусть отображает на все и . Тогда для любого , найдется , такой что и

.▄

Приведем для задачи с ограничениями типа равенства необходимые условия локального минимума (аналог теоремы 11).

Теорема 13. (Теорема Куна-Таккера для нелинейной задачи с ограничениями типа равенства). Пусть - точка локального минимума задачи , и ее ограничения в этой точке удовлетворяют условию Люстерника, тогда найдется вектор , такой, что будет выполнено

,

где - оператор, сопряженный , действующий из в .▄

Упражнение 1. Доказать теорему 13, используя теорему Люстерника. ▄

Условия локального экстремума высших порядков

Будем продолжать рассматривать задачу 4, в предположении, что в точке функции и дифференцируемы нужное число раз, их -е производные в точке будем обозначать через и (полилинейная функция действует из в ), и ограничения задачи в точке удовлетворяют условию Слейтера.

Пусть - точка локального минимума задачи 4. Через будем обозначать множество множителей Лагранжа задачи 4, т.е., множество , для которых выполнено (20). Теорема 11 гарантирует нам непустоту множества .

Упражнение 2. Доказать замкнутость . Используя выполнение условия Слейтера, доказать ограниченность .▄

Определение 13. Введем множества критических направлений порядка следующим образом:

.▄

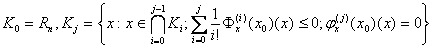Приведем без доказательства необходимые и достаточные условия локального минимума высших порядков.

Теорема 14. (Необходимые условия локального экстремума) Пусть невырожденная точка есть точка локального минимума задачи 4, тогда для любого натурального справедливо:

,

(22)

где - -я частная производная по функции Лагранжа задачи 4 в точке .▄

Теорема 15. (Достаточные условия строгого локального экстремума. Теорема верна для конечномерных пространств). Пусть - допустимая точка задачи 4. Пусть при выполнено (22) и найдется число , такое что

,

тогда точка доставляет строгий локальный минимум задаче 4. ▄