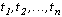 выборка случайных величин
выборка случайных величин 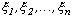 , где
, где 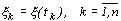 , описывается совместной нормальной плотностью вероятности
, описывается совместной нормальной плотностью вероятностиПроцесс, реализации которого, полученные в идентичных условиях, не совпадают друг с другом, называют случайным. Координата случайного процесса является случайной величиной, которая описывается многоточечной функцией распределения или соответствующей функцией плотности вероятности. Для стационарного случайного процесса функция распределения или функция плотности вероятности инвариантна относительно операции сдвига во времени. Математические модели случайных процессов широко используются как для описания полезных сигналов, так и сигналов помех. Наиболее известной моделью случайного процесса является гауссовский случайный процесс [1].
Случайный процесс ![]() (t)} называют гауссовским, если для любого конечного множества моментов времени
(t)} называют гауссовским, если для любого конечного множества моментов времени 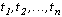 выборка случайных величин
выборка случайных величин 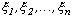 , где
, где 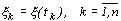 , описывается совместной нормальной плотностью вероятности
, описывается совместной нормальной плотностью вероятности
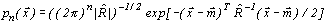 , , | (3.1) |
где
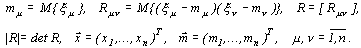
Гауссовский случайный процесс полностью определяется своим средним значением 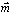 и функцией корреляции
и функцией корреляции 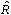 . Приведем некоторые свойства гауссовского случайного процесса.
. Приведем некоторые свойства гауссовского случайного процесса.
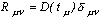 ,
,
где 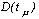 - дисперсия,
- дисперсия, 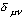 - символ Кронеккера, то
- символ Кронеккера, то
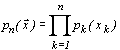 .
.
где 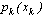 - одноточечная функция плотности вероятности.
- одноточечная функция плотности вероятности.
Стационарный гауссовский случайный процесс с абсолютно независимыми значениями называют белым шумом. Белый шум имеет нулевое среднее значение и ![]() -образную функцию корреляции, которой соответствует равномерная спектральная плотность мощности в широком частотном диапазоне.
-образную функцию корреляции, которой соответствует равномерная спектральная плотность мощности в широком частотном диапазоне.
Отметим, что если на вход линейной системы воздействует произвольный случайный процесс с ограниченной дисперсией, то процесс, наблюдаемый на выходе линейной системы, будет иметь асимптотически нормальное распределение. Это утверждение известно как явление нормализации случайных процессов и является прямым следствием центральной предельной теоремы [2].
Из этого утверждения следует, если белый шум пропустить через линейный фильтр, то спектральная плотность мощности полученного процесса будет равна произведению квадрата модуля частотной характеристики этого фильтра на спектральную плотность мощности белого шума.
В качестве примера явления нормализации случайных процессов [3] рассмотрим выражение для плотности вероятности суммы n независимых равномерно распределенных на интервале (0,1) случайных величин
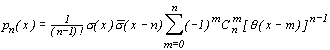 , , | (3.2) |
где
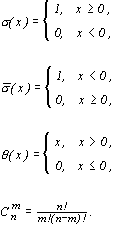
Среднее значение и дисперсия этого распределения соответственно равны 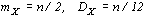 . Численные расчеты показывают, что функция плотности вероятности (4.2) практически не отличается от нормальной кривой при n > 10.
. Численные расчеты показывают, что функция плотности вероятности (4.2) практически не отличается от нормальной кривой при n > 10.
Источником равномерно распределенных на интервале (0,1) случайных величин может служить любой стандартный генератор псевдослучайных чисел с равномерной плотностью вероятности, например, простой генератор псевдослучайных чисел, предложенный Пайком и Хиллом [4].
Моделирование широкополосного шума производится с помощью обработки белого шума линейным фильтром, квадрат модуля частотной характеристики которого совпадает со спектром мощности широкополосного шума.
Реальные сигналы в той или иной степени всегда искажены шумом. Если уровень шума превышает допустимый порог, то становится трудно выделить полезный сигнал. В таких случаях требуется специальная обработка сигнала, которую называют шумоподавлением.
Задача подавления шума или, более точно, задача фильтрации сигнала из смеси с шумом, представляет одну из актуальных задач цифровой обработки сигналов. Сложность данной задачи состоит в том, что в реальном сигнале обычно довольно трудно отделить шум от некоторых составляющих полезного сигнала. Вследствие этого практически все известные методы подавления шума в той или иной степени приводят к искажению полезного сигнала.
Одним из наиболее математически развитых методов фильтрации сигнала из смеси с шумом является метод оптимальной линейной фильтрации Винера-Колмогорова [5,6]. Ниже рассматриваются алгоритмы шумоподавления, разработанные на основе этого метода.
Постановка задачи. Пусть наблюдаемый сигнал 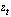 представляет смесь полезного сигнала
представляет смесь полезного сигнала 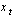 с сигналом помехи, которую представляет широкополосный шум
с сигналом помехи, которую представляет широкополосный шум 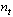 :
:
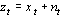 . . | (3.3) |
Будем предполагать, что полезный сигнал и сигнал помехи удовлетворяют модели гауссовского случайного процесса с нулевым средним значением, причем полезный сигнал является независимым от сигнала помехи. Требуется найти оптимальный фильтр для выделения полезного сигнала из смеси с сигналом помехи.
Одноточечный шумоподавитель. Определим интервал времени Т, на котором априори с удовлетворительной точностью выполняется условие декоррелированности полезного сигнала и шума, т.е.
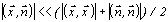 , , | (3.4) |
где
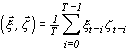
- взаимная корреляционная функция, 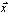 ,
, 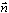 - выборки значений координаты полезного сигнала и шума на интервале времени Т.
- выборки значений координаты полезного сигнала и шума на интервале времени Т.
Определим оценку текущего значения полезного сигнала из смеси с шумом 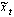 в виде произведения текущего значения наблюдаемого сигнала
в виде произведения текущего значения наблюдаемого сигнала 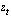 на некоторый корректирующий коэффициент
на некоторый корректирующий коэффициент 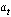 :
:
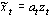 . . | (3.5) |
Оптимальную оценку текущего значения корректирующего коэффициента 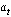 найдем из условия
найдем из условия
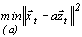 , , | (3.6) |
где
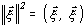 .
.
Минимизируя (3.6) по параметру а, получим
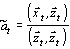 . . | (3.7) |
Учитывая условие декоррелированности полезного сигнала и шума (3.4), оптимальную оценку текущего значения корректирующего коэффициента можно записать в виде
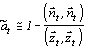 , , | (3.8) |
где второе слагаемое представляет отношение оценки дисперсии шума к оценке дисперсии наблюдаемого сигнала. Заменив оценку дисперсии шума ее значением и подставив (3.8) в (3.5), получим формулу обработки сигнала одноточечным шумоподавителем
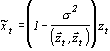 , , | (3.9) |
где 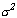 - дисперсия помехи.
- дисперсия помехи.
Принцип действия одноточечного шумоподавителя достаточно простой: при больших значениях дисперсии наблюдаемого сигнала корректирующий коэффициент 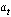 приблизительно равен единице и оценка полезного сигнала (3.9) практически совпадает с исходным сигналом; при малых значениях дисперсии наблюдаемого сигнала, которые обычно соответствуют паузам аудиосигнала, корректирующий коэффициент
приблизительно равен единице и оценка полезного сигнала (3.9) практически совпадает с исходным сигналом; при малых значениях дисперсии наблюдаемого сигнала, которые обычно соответствуют паузам аудиосигнала, корректирующий коэффициент 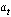 уменьшается вплоть до нуля и оценка полезного сигнала представляет исходный сигнал уменьшенной амплитуды.
уменьшается вплоть до нуля и оценка полезного сигнала представляет исходный сигнал уменьшенной амплитуды.
Можно показать, что дисперсия обработанного шумоподавителем сигнала меньше дисперсии наблюдаемого сигнала приблизительно на величину дисперсии помехи.
Наилучшие результаты обработки сигнала одноточечным шумоподавителем достигаются при подавлении помехи типа белого шума. В других случаях, когда, например, спектр мощности широкополосной помехи расположен в определенной полосе частот, лучшие результаты можно получить, если придерживаться следующей схемы комплексной обработки сигнала:
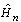 , квадрат модуля частотной характеристики которого аппроксимирует спектр мощности широкополосной помехи;
, квадрат модуля частотной характеристики которого аппроксимирует спектр мощности широкополосной помехи;
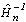 ;
;
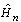 ;
;
Рассмотренная схема описывает последовательность действий, суть которых состоит в преобразовании частотной характеристики наблюдаемого сигнала с целью декорреляции широкополосной помехи, обработки сигнала шумоподавителем и восстановлении исходной частотной характеристики полезного сигнала.
Многоточечный шумоподавитель. Для оценивания текущего значения полезного сигнала можно использовать более сложные многоточечные линейные оценки типа
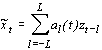 , , | (3.10) |
где {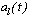 } - коэффициенты корректирующего линейного фильтра.
} - коэффициенты корректирующего линейного фильтра.
Оптимальные значения коэффициентов корректирующего фильтра, как и в случае одноточечного шумоподавителя, определяют из условия
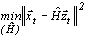 , , | (3.11) |
где 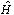 представляет компактное выражение импульсной характеристики корректирующего фильтра:
представляет компактное выражение импульсной характеристики корректирующего фильтра:
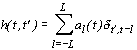 .
.
Минимизируя (3.11) по параметрам {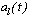 }, получим систему нормальных уравнений
}, получим систему нормальных уравнений
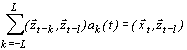 , , | (3.12) |
которая является линейной относительно искомых параметров.
Если сигнал помехи представляет белый шум, то систему нормальных уравнений (3.12) можно записать в виде
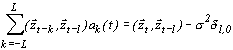 , , | (3.13) |
где 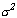 - дисперсия шума. Корреляционная матрица системы (3.13) имеет вид
- дисперсия шума. Корреляционная матрица системы (3.13) имеет вид
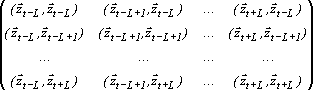 . . | (3.14) |
Решение системы линейных уравнений (3.13) можно найти с помощью вычисления обратной корреляционной матрицы. Определитель матрицы должен быть отличен от нуля [7]. Искомые параметры вычисляются по формуле
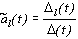 , , | (3.15) |
где ![]() (t) - определитель корреляционной матрицы (3.14),
(t) - определитель корреляционной матрицы (3.14), 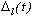 - определитель матрицы (3.14), в которой l-й столбец заменен на столбец {
- определитель матрицы (3.14), в которой l-й столбец заменен на столбец {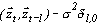 }.
}.
Подставив оптимальную оценку текущих значений коэффициентов корректирующего фильтра (3.15) в (3.10), получим общую формулу обработки сигнала многоточечным шумоподавителем. Приведем явные выражения для коэффициентов трехточечного оптимального корректирующего фильтра:
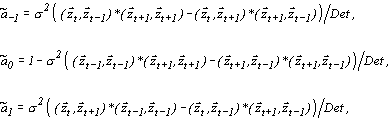 | (3.16) |
где
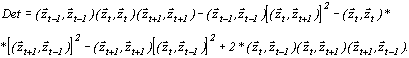
Принцип действия многоточечного шумоподавителя аналогичен принципу действия одноточечного шумоподавителя. Как и в случае одноточечного шумоподавителя, наилучшие результаты обработки сигнала многоточечным шумоподавителем достигаются при подавлении помехи типа белого шума. В остальных случаях следует придерживаться приведенной выше схемы комплексной обработки сигнала. Аудиозапись рекомендуется обрабатывать итеративно в несколько проходов, при этом в качестве параметра фильтра 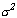 выбирать нижнюю границу оценки дисперсии шума.
выбирать нижнюю границу оценки дисперсии шума.
1. Левин Б.Р. Теоретические основы статистической радиотехники. М.: Радио и связь, 1989.
2. Левин Б.Р., Шварц В. Вероятностные модели и методы в системах связи и управления. М.: Радио и связь, 1985.
3. Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982.
4. Pike M.C., Hill J.D. Algorithm 266, Psevdo Random Numbers (65), Collected Algorithms from CACM, July 1965.
5. Колмогоров А.Н. Интерполирование и экстраполирование стационарных случайных последовательностей. // Изв. АН СССР. Сер. Математическая 1941, No 5. С. 3-14.
6. Winer N. The interpolation, extrapolation and smoothing of stationary time series. // N.Y.: J. Wiley, 1949, 162 p.
7. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.