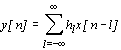, Под термином "цифровая фильтрация" обычно понимают локальную цифровую обработку сигнала скользящим окном или аппертурой. При этом полагают, что размер окна много меньше размера выборки обрабатываемого фрагмента сигнала. Для каждого положения окна, за исключением, возможно, небольшого числа крайних точек выборки, выполняются однотипные действия, которые определяют так называемый отклик или выход фильтра. Если действия, определяющие отклик фильтра, не изменяются в процессе перемещения по выборке сигнала, то соответствующий фильтр называется стационарным. В противном случае фильтр называется нестационарным. Различают линейную и нелинейную цифровую фильтрацию.
Линейная цифровая система описывается уравнением свертки
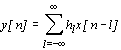| , | (2.1) |
где x[n] - входная выборка, y[n] - выходная выборка,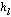 
- импульсная характеристика системы. Передаточная функция линейной цифровой системы определяется выражением
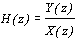 , | (2.2a) |
где
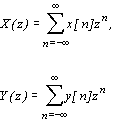
- z-преобразования входной и выходной выборок сигнала. Если умножить обе части равенства (2.1) на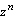 
и просуммировать по n, можно получить выражение для передаточной функции линейной цифровой системы в виде
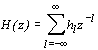 , | (2.2б) |
где 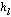- импульсная характеристика системы.
Необходимое и достаточное условие устойчивости линейной цифровой системы [1] часто записывается в виде неравенства для импульсной характеристики системы
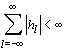 . | (2.3) |
Линейная цифровая система является физически реализуемой, если
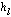=0 при l<0.
Цифровые устройства, выполняющие преобразования вида (2.1) называются линейными цифровыми фильтрами. Линейный цифровой фильтр является финитной линейной цифровой системой, и, в общем случае, описывается уравнением
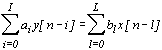 , | (2.4) |
где {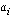
, 
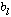} - коэфициенты фильтра. Обычно линейные цифровые фильтры подразделяют на фильтры низких частот, фильтры высоких частот, полоснопропускающие и полоснозаграждающие (режекторные) фильтры, амплитудные и фазовые фильтры-корректоры, гребенчатые фильтры и др. Первые четыре типа фильтров называют основными или базовыми типами фильтров. По своей конструкции линейные цифровые фильтры разделяют на рекурсивные и нерекурсивные (трансверсальные) фильтры. Коэфициенты трансверсальных фильтров или фильтров с конечной импульсной характеристикой (КИХ-фильтров) удовлетворяют условиям:
{
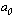=1,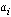 
=0 для всех i#0}.
Цифровые фильтры, которые не являются трансверсальными, называются рекурсивными или фильтрами с бесконечной импульсной характеристикой (БИХ-фильтрами).
Передаточная функция линейного цифрового фильтра (2.4) имеет вид
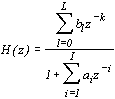 . | (2.5) |
Многочлены стоящие в числителе и знаменателе этого выражения можно представить в виде произведения и переписать передаточную функцию линейного цифрового фильтра (2.4) в следующем виде
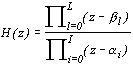 . | (2.6) |
Условие устойчивости линейного цифрового фильтра обычно записывают в виде неравенства:
,
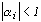i=0,1,...,I , т. е. полюса передаточной функции цифрового фильтра должны лежать внутри окружности единичного радиуса. Положение нулей передаточной функции {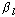
} на устойчивость фильтра не влияет, однако условие
|
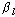| ‹ 1, l=0,1,...,L
определяет минимально-фазовый цифровой фильтр.
Частотная характеристика цифрового фильтра H(w)соответствует передаточной функции фильтра H(z) при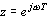 
, где T - интервал дискретизации, w = 2*3.14...*f - круговая частота. Поскольку экспоненциальная функция мнимого аргумента 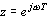является периодической функцией частоты с периодом W = 2*3.14.../T, то частотная характеристика цифрового фильтра H(w) также является периодической функцией частоты с периодом W.
Вычисление коэфициентов цифрового фильтра удовлетворяющего заданным условиям принято называть проектированием (синтезом) фильтра, а устройство или программу, которая осуществляет преобразование цифровых сигналов - реализацией фильтра.
Постановка задачи проектирования цифрового фильтра следующая: априори задан модуль или квадрат модуля желаемой частотной характеристики фильтра. Требуется найти коэфициенты фильтра, квадрат модуля частотной характеристики которого удовлетворительно аппроксимирует квадрат модуля желаемой частотной характеристики при заданных ограничениях. В частности, такими ограничениями могут являться: тип фильтра, число коэффициентов (порядок) фильтра, ошибка аппроксимации и др. Ниже рассматриваются способы конструирования некоторых типов цифровых фильтров.
Наиболее простым способом проектирования КИХ-фильтров является синтез цифрового фильтра методом взвешивания с помощью формирующего окна [1]. Этот способ является очень полезным в приложениях, где простота проектирования фильтра оказывается важнее его эффективности. Сущность этого способа проектирования фильтра состоит в следующем. Известно, что частотная характеристика цифрового фильтра H(w) является периодической функцией частоты, поэтому может быть представлена рядом Фурье
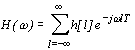 , | (2.7) |
где
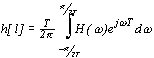 | (2.8) |
- импульсная характеристика фильтра, Т - интервал дискретизации.
Импульсная характеристика фильтра, соответствующая желаемой частотной характеристике, обычно инфинитна и, поэтому, практически нереализуема. Чтобы построить практически реализуемый КИХ-фильтр можно просто ограничить область изменения импульсной характеристики фильтра h[l] по аргументу l некоторым априори выбранным значением L. Другими словами, положить h[l]= 0, при |l|>L. Частотная характеристика полученного таким способом КИХ-фильтра будет аппроксимировать желаемую частотную характеристику H(w). Такое простое усечение ряда (2.7) имеет, однако, недостаток, который известен как явление Гиббса [2].
Явление Гиббса состоит в том, что обрыв h[l] приводит к тому, что аппроксимирующая частотная характеристика будет иметь резкие выбросы в виде пульсаций вблизи переходов желаемой частотной характеристики фильтра от полосы пропускания к полосе поглощения. Чтобы уменьшить величину этих пульсаций, на практике используют импульсные характеристики фильтров, которые конструируются как произведение "идеальной" импульсной характеристики (2.8), соответствующей желаемой частотной характеристике фильтра, на некоторую функцию, так называемое "окно" w[l].
В качестве окна обычно выбирают гладкую колоколообразную функцию стремящуюся к нулю при l стремящимся к L. В результате этой операции достигается уменьшение величины пульсаций за счет изменения крутизны и некоторого уширения полосы пропускания частотной характеристики фильтра.
Процедура вычисления коэфициентов КИХ-фильтра состоит в следующем:
В результате получим коэффициенты искомого КИХ-фильтра.
К настоящему времени предложено много различных оконных функций [3], свойства которых исследовались их авторами, в частности, "окно" Хэмминга, "окно" Кайзера, "окно" Долфи-Чебышева и др. В качестве примера приведем формулу [4] для вычисления функции окна Поттера:
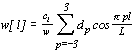 , | (2.9) |
где
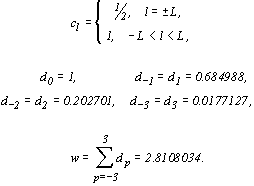
Запишем передаточную функцию линейного цифрового фильтра (2.6) в следующем виде
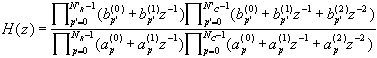 , | (2.10) |
где числитель и знаменатель передаточной функции представлены в виде произведений многочленов первой и второй степени с действительными коэфициентами относительно переменной z; параметры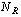 
▓, 
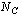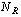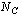▓, , характеризуют число действительных и комплексно-сопряженных пар корней числителя и знаменателя.
Квадрат модуля частотной характеристики (2.10) можно представить выражением
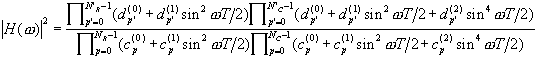 , | (2.11) |
где
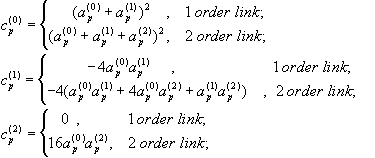 | (2.12) |
и аналогичные выражения для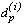 
- параметров. Система нелинейных уравнений (2.12) связывает параметры частотной характеристики {
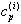} с коэфициентами фильтра {
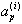}. В общем случае зависимость коэфициентов фильтра от параметров частотной характеристики описывается довольно громоздким выражением. Поэтому коэфициенты цифрового фильтра обычно вычисляют по характерным параметрам каждого конкретного типа фильтра непосредственно.
Одним из наиболее простых и полезных рекурсивных цифровых фильтров является фильтр Баттерворда. Квадрат модуля амплитудно-частотной характеристики аналогового прототипа базового фильтра низких частот Баттерворда описывается выражением [1]
,
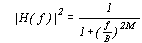где B - ширина полосы пропускания фильтра, М - порядок фильтра. Частотную характеристику цифрового фильтра получают из амплитудно-частотной характеристики аналогового прототипа с помощью некоторого преобразования частотной шкалы. Основное условие, которому должно удовлетворять это преобразование, состоит в том, чтобы частотная характеристика полученного цифрового фильтра являлась периодической функцией частоты с периодом W = 2*3.14.../Т, где Т - интервал дискретизации.
Широко известны два типа цифровых фильтров Баттерворда: синусный фильтр Баттерворда с базовым фильтром низких частот
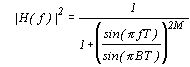 , | (2.13) |
и тангенсный фильтр Баттерворда с базовым фильтром низких частот
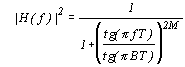 . | (2.14) |
По сравнению со своим аналоговым прототипом, синусный фильтр Баттерворда имеет более гладкие, а тангенсный фильтр - более крутые переходы от полосы пропускания к полосе поглощения фильтра.
Рассмотрим схему расчета коэфициентов этих фильтров. Нам потребуется формула
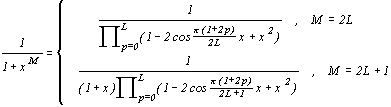 | (2.15) |
Доказательство этой формулы элементарное. Действительно, знаменатель функции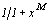 
можно представить в виде произведения
,
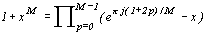где {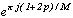 
, p= 0,1,...,M-1 } - корни уравнения 
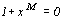. Собирая вместе множители с комплексно-сопряженными корнями, получаем формулу (2.15).
Подставяя в (2.15) выражение
,
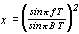получим
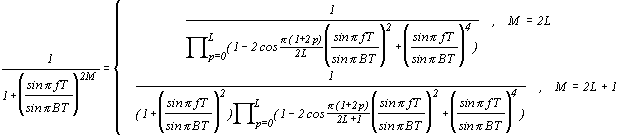
Сравнивая это выражение с (2.11), находим параметры частотной характеристики 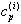, по которым, решая систему уравнений (2.12), вычисляем коэфициенты синусного фильтра Баттерворда.
Аналогично, подставив в (2.15)
,
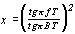и записав тангенс через синус, используя формулу
,
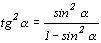находим выражение для квадрата модуля частотной характеристики тангенсного фильтра Баттерворда в виде (2.11). Из этого выражения определяем параметры частотной характеристики 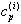и, решая систему уравнений (2.12), вычисляем коэфициенты тангенсного фильтра Баттерворда.
Устройство реализующее цифровой фильтр выполняет последовательное умножение входной и/или выходной выборки сигнала на коэфициенты фильтра и сложение полученных произведений. Структурная схема рекурсивного цифрового фильтра 2-го порядка показана на рис. 1.
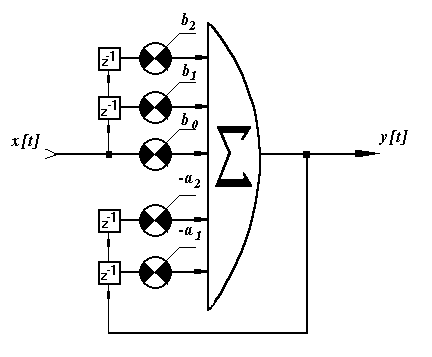
Рис. 1. Структурная схема линейного цифрового фильтра 2-го порядка.
Цифровые фильтры более высоких порядков можно реализовать несколькими способами. Наиболее простым способом является так называемая прямая форма реализации цифрового фильтра. В прямой форме цифровые фильтры реализуют в соответствии с формулой (2.5). Структурная схема цифрового фильтра в этом случае аналогична схеме, показанной на рис.1, но имеет большее число линий задержек и умножителей.
Другим способом реализации цифровых фильтров является каскадная форма. При реализации цифрового фильтра в каскадной форме, цифровой фильтр представляют в виде последовательности следующих друг за другом цифровых фильтров 1-го или 2-го порядка. В этом случае цифровые фильтры реализуют в соответствии с формулой (2.10).
Представление цифрового фильтра в прямой форме обычно используется для реализации КИХ-фильтров, тогда как представление фильтра в каскадной форме чаще применяется для реализации БИХ-фильтров.
Заметим, что исходные данные для обработки краевых значений выборки сигнала в соответствии с формулой фильтра могут оказаться неопределеными, поэтому их обработку приходится выполнять отдельно. Редукцию общей формулы обработки сигнала на краях выборки принято называть краевым эффектом. Обычно различают три схемы обработки краевых значений [5] :
P - схема обработки ограничивается фильтрацией центральной части выборки, оставляя края сигнала необработанными. В результате выходная выборка оказывается меньшего размера, чем исходная выборка.
S - схема производит обработку всей входной выборки, при этом требуемые в соответствии с заданной формулой обработки неопределенные значения выборки сигнала полагают равными нулю. Размер выходной выборки соответствует размеру исходной выборки.
T - схема аналогична S - схеме за исключением того, что неопределенные значения выборки сигнала полагают равными соответствующим значениям, расположенным на противоположном конце выборки. Иными словами, полагают, что выборка является виртуальной периодической функцией с периодом равным размеру исходной выборки. Размер выходной выборки в этом случае также соответствует размеру исходной выборки. Выбор какой-либо схемы обработки краевых значений обычно определяется контекстом решаемой задачи.
Класс нелинейных цифровых фильтров является слишком широким для того, чтобы проводить его изучение в общем виде. Поэтому ограничимся рассмотрением одного из самых известных семейств нелинейных цифровых фильтров, а именно, семейства порядковых фильтров. Порядковые фильтры широко используются в задачах цифровой обработки сигналов и изображений, в частности, для обнаружения объектов, выделения границ, подавления импульсных помех. Отклик порядкового p-фильтра определяется как p-я порядковая статистика [6], т. е. элемент под номером p, где p-один из {0,1,...,N-1} , N - размер аппертуры фильтра, в вариационном ряду, полученному из выборки исходных данных, находящихся в пределах аппертуры фильтра. В частности, при p=0 и p=N-1 выходная выборка будет описывать соответственно "нижнюю" и "верхнюю" огибающие сигнала, а при p=N/2 выходная выборка будет представлять результат медианной фильтрации сигнала.
1. Каппелини В., Константинидис Дж., Эмилиани П. Цифровые фильтры и их применение. М.: Энергоатомиздат, 1983.
2. Хемминг Р.В. Цифровые фильтры. М.: Недра, 1987.
3. Рабинер Л.Р., Гоулд В. Теория и применение цифровой обработки сигналов. М.: Мир, 1978.
4. Отнес Р., Эноксон Л. Прикладной анализ временных рядов. Основные методы. М.: Мир, 1982.
5. Яншин В.В., Калинин Г.А. Обработка изображений на языке С для IBM PC: Алгоритмы и программы. М.: Мир, 1994.
6. Дэйвид Г. Порядковые статистики. М.: Наука, 1979.